1. Подання основних елементарних функцій по формулі тейлора

Ми застосуємо формулу Тейлора до функцій е^х, cosx, sinx, ln(l + x), (1 + х) ^а. Всі вони нескінченно диференційовані в околиці крапки хо = ПРО, і виходить, до них застосовна формула Тейлора при кожному п. (Формула Тейлора, виписана в точці хо = 0, називається формулою Маклорена.)

Функція е^х.

Тоді маємо

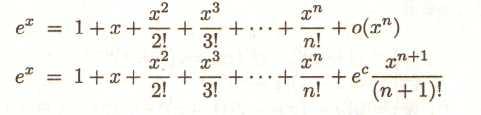(60),

(61)

Функція cosx.

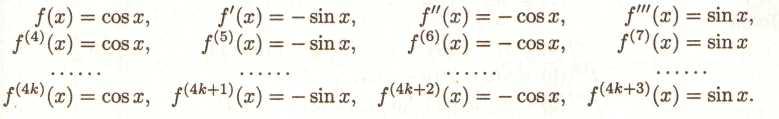
Тоді

Виходить,

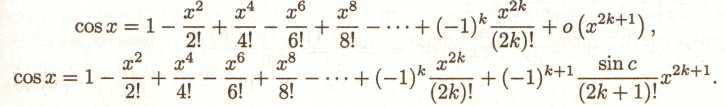(62),

(63)

Функція sin x. Зовсім аналогічно п. 9.1 одержуємо

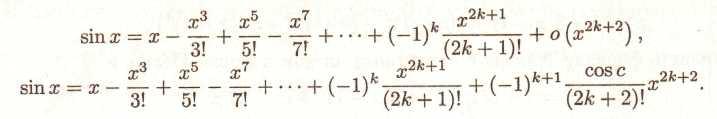(64),

(65)

Функція ln(1 + х). Знайдемо f'(x), f"(x), f⁽³⁾(x), ...

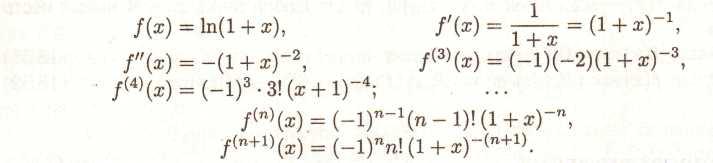
Тоді

Застосовуючи формулу Тейлора (48) і (50), одержуємо

(66),

(67)

Функція (1 + х) ^а, а € R.

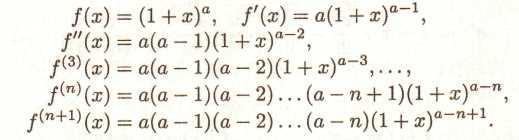
Тоді

Тоді по формулах (48) і (50) одержуємо

(68)

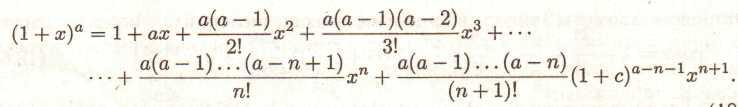(69)

Застосування формули Тейлора для обчислення меж.

Визначення 4. Головною частиною функції f при х → х_о називається перший ненульовий доданок у її багаточлені Тейлора, побудованому в точці х_о.

Зауваження. Відносно функції f ми, звичайно, думаємо, що для неї справедлива формула Тейлора в деякій околиці крапки х_о

Нехай головний член функції / має вигляд а(х — хо)^до, тоді

(70)

т. е. ми виписали формулу Тейлора порядку до для функції f. Допустимо, нам необхідно обчислити

т. е. ми маємо невизначеність виду .

Випишемо формулу Тейлора для f(x) і g(х), обмежившись головними членами розкладання:

Ясно, що має місце співвідношення

(71)

ПРИКЛАД 18.7. Обчислити

Розкладемо функції x—sin а;, е^2х -1 — 2х - 2х² по формулі Тейлора в околиці крапки 0, взявши п = 3:

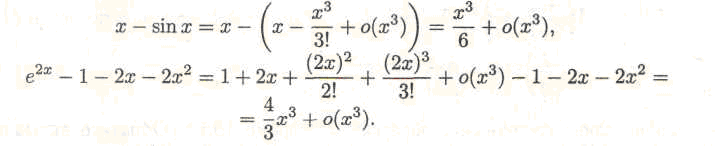
Виходить,

Застосування формули Тейлора в наближених обчисленнях. Формулу Тейлора, як і формулу (14) лінеаризації функції, застосовують у наближених обчисленнях. Якщо ми можемо виписати для функції f в околиці крапки х₀ формулу Тейлора порядку п, то думають

(72)

при цьому f(x) — (P_n(f))(x) = o((x — х_о)ⁿ), а якщо ми перебуваємо в умовах, коли можна виписати формулу Тейлора із залишковим членом у формі Лагранжа, то має місце оцінка погрішності

(73)

ПРИКЛАД 8. Обчислити приблизно значення ln(1,2), застосувавши формулу Тейлора 3-го порядку.

По формулі (67) маємо

У нашому випадку х= 0,2. Тоді

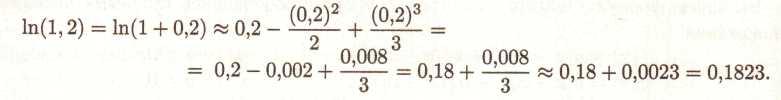
Оцінимо погрішність за допомогою формули (73)

Контрольні питання й завдання

1. Чи є функція в = |х| диференційованою у точці: а) х = 0; б) х = 1; в) х = -2?

2. Сформулюйте найпростіші правила диференціювання:

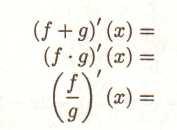
3. Чи справедлива теорема, зворотна до теореми 1? (Зверніть увагу на питання 1, п. а).)

4. Приведіть самостійно негеометричний доказ теореми 6.

5. Обчислите приблизно за допомогою диференціала .

6. Чи можна вказати таку складну функцію й крапку її області визначення, у якій має місце інваріантість другого диференціала?

ДОСЛІДЖЕННЯ ФУНКЦІЙ ЗА ДОПОМОГОЮ ПОХІДНИХ

Вивчення характеру поводження функції й побудова її графіка — одна з найважливіших задач математичного аналізу. У цій главі ми будемо припускати, що функції визначені на інтервалі (а,b) (або об'єднанні кінцевого числа інтервалів), безперервні на інтервалі або мають на ньому кінцеве число точок розриву, диференційовані на (а,b) або на (а,b) є лише кінцеве число точок, у яких функція не є диференційованою.