Визначник добутку матриці

Теорема: визначник добутку двох квадратних матриць n-го порядку дорівнює добутку їх визначників, тобто

Перевіримо для матриць другого порядку

Обернена матриця

Означення: Матриця А називається неособливою (не виродженою), якщо її визначник відмінний від нуля, тобто . Якщо , тоді матриця називається особливою (виродженою).

Означення: Квадратна матриця називається оберненою до матриці А, якщо виконується рівність

,

де Е – одинична матриця.

Алгоритм знаходження оберненої матриці

1. Обернена матриця існує тільки до квадратної невиродженої матриці , тому обчислюємо визначник матриці і впевнюємося, що .

2. Знайдемо алгебраїчні доповнення до елементів матриці А за формулою і складемо матрицю , елементами якої є алгебраїчні доповнення

.

3. Знайдемо матрицю транспоновану до матриці , для цього поміняємо рядки та стовпці місцями

.

4. Знайдемо обернену матрицю за формулою .

.

5. Зробимо перевірку .

Приклад: Знайти матрицю , обернену до матриці

1.

Матриця А є невиродженою, тому існує матриця обернена до матриці А.

2. Знайдемо алгебраїчні доповнення до елементів матриці А.

Складемо матрицю , елементами якої є алгебраїчні доповнення

.

3. Знайдемо матрицю транспоновану до матриці

.

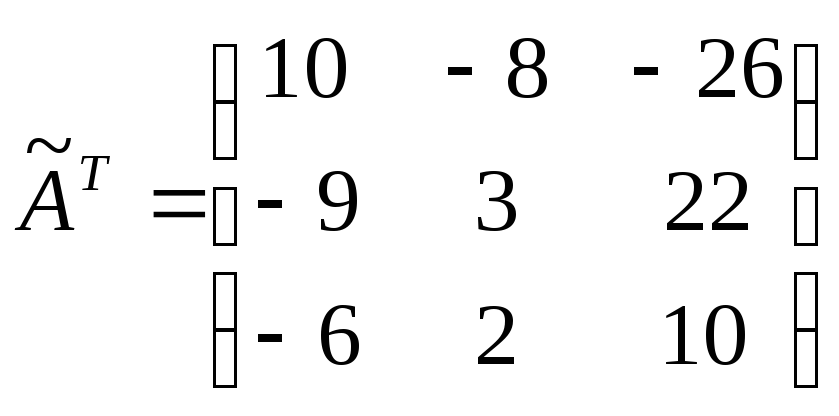4. Знайдемо обернену матрицю

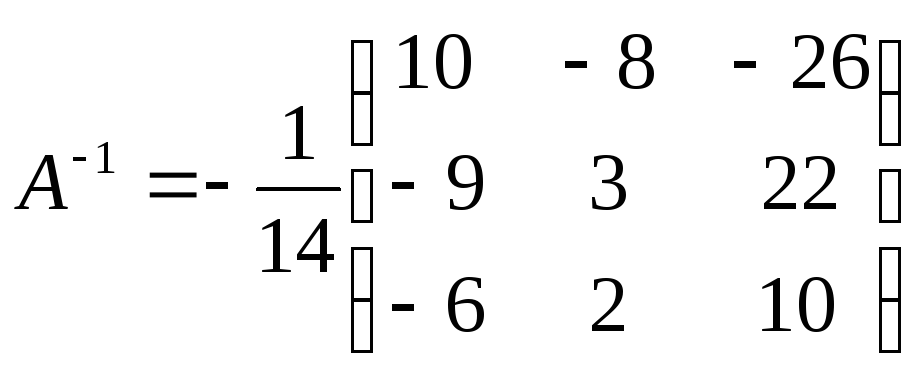
5. Зробимо перевірку

.

Розв’язування слар матричним способом

Розглянемо розв’язування СЛАР матричним способом на прикладі системи

Складемо матрицю системи 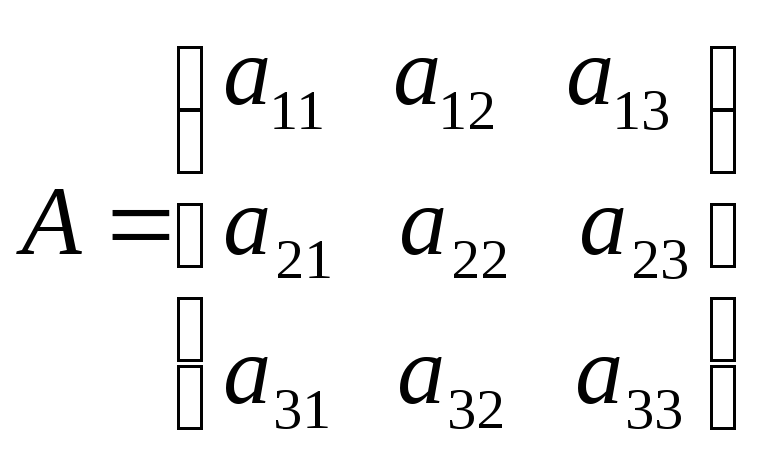, матрицю-стовпець вільних членів і матрицю-стовпець невідомих .

Знайдемо добуток матриць

.

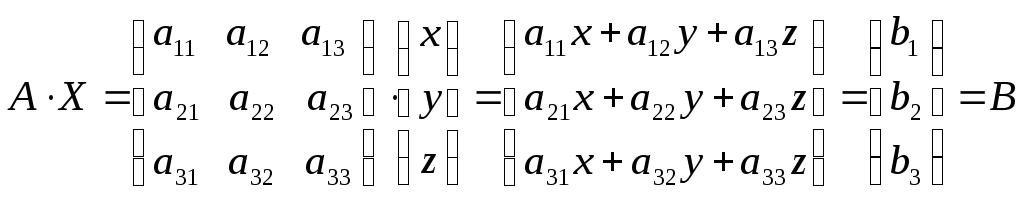Домножимо обидві частини виразу на і одержимо

,

Враховуючи, що , маємо

Приклад: Розв’язати систему лінійних рівнянь матричним способом

Складемо матриці ; ; .

Знайдемо за вищевикладеним алгоритмом матрицю, обернену до матриці А

.

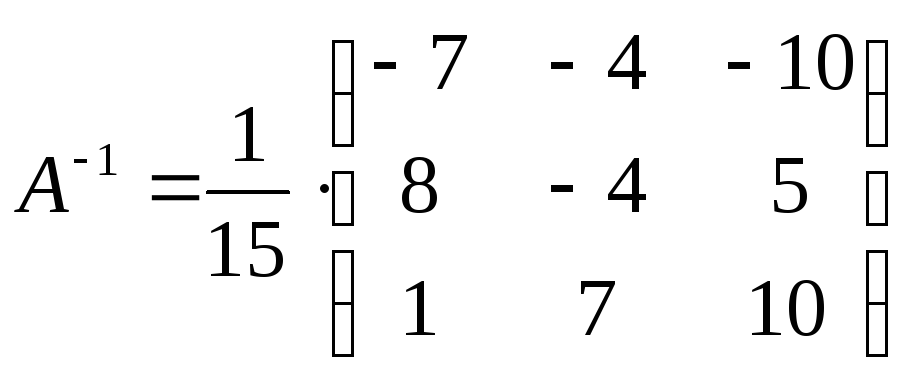За формулою знайдемо розв’язок СЛАР

.

Відповідь:

Тема 2 Векторна алгебра Вектори

Означення: Вектором називається направлений відрізок з початком у точці А і кінцем у точці В.

Довжиною або модулем вектора називається число , яке дорівнює довжині відрізка АВ, який є зображенням вектора .

Вектори, що лежать на одній прямій або на паралельних прямих, називаються колінеарними.

Вектори, що належать одній і тій же площині або паралельним площинам, називаються компланарними.

Якщо початок вектора і його кінець співпадають, тобто маємо вектор , то такий вектор називається нульовим і позначається , а його модуль .

Рівними називаються два вектори, якщо вони задовольняють умовам:

1) вони є колінеарними;

2) їх модулі є рівними;

3) вони є співнапрямленими , .

Якщо і вектори є протилежно напрямленими , тоді вектори і називаються протилежними.

Вектор, модуль якого дорівнює одиниці називається одиничним або ортом і позначається , .