2. Тригонометрична форма комплексного числа.

Нехай (, ) – полярні координати точки M(x, y) Використовуючи зв'язок між полярними та прямокутними (декартовими) координатами точки на площині

x = cos , y = sin ,

запишемо КЧ у вигляді

z = (cos  + isin )

3. Показникові форма комплексного числа. Формули Ейлера.

4. Деякі застосування комплексних чисел.

Розглянемо використання комплексних чисел для розрахунку електричних кіл. Використання комплексних чисел дає можливість впроваджувати всі закони, формули і методи розрахунків, що застосовуються в колах постійного струму, для розрахунку кіл змінного струму, спростити деякі розрахунки, замінивши графічне розв’язування з використанням векторів на алгебраїчне; розраховувати складні кола, такі, що іншим шляхом розрахувати не можливо, і, нарешті, уніфікувати обчислення кіл постійного й змінного струмів.

Рівняння змінної напруги в загальному вигляді записується так:

u =U_М sin (w t + y), (4. 1)

де u – миттєве значення напруги; U_М – максимальне значення (амплітуда) напруги;

• – кутова частота; при стандартній частоті 50 Гц w =314 рад/с або 18000 град/с;

t – час;

y - початковий фазовий кут;

w t = a – так званий електричний кут.

Це рівняння пов’язує дві змінні величини: напругу u і час t. З плином часу напруга змінюється синусоїдально. Графік рівняння (1) зображений на рис. 1 [1].

Аналогічний вигляд мають рівняння (і графіки) інших величин, які змінюються синусоїдально:

струму i=I_М sin(w t + y);

е.р.с. е =E_М sin(w t + y) та ін.

При розрахунку кіл змінного струму доводиться виконувати додавання, віднімання, множення і ділення рівнянь зазначеного вище типу. Наприклад, є два генератори, з’єднаних послідовно (рис. 2). Визначити напругу на затискачах кола, тобто сумарну напругу.

Перший генератор дає напругу и₁=U_М1 sin(w t + y₁), другий – u₂=U_М2 sin(w t + y₂). (Тут і надалі розглядаються синусоїдальні величини, що мають однакову кутову частоту w.)

Рис. 4.1

Щоб одержати напругу між клемами а і b, треба скласти задані напруги:

u = u₁ + u₂, або u = U_М1 sin(w t + y₁) + U_М2sin(w t + y₂).

У результаті додавання двох синусоїдальних коливань з однаковою кутовою частотою виходить рівняння синусоїди з тією самою кутовою частотою:

u =U_М sin(ωt + ψ),

де U_м=;

ψ= arctg .

Однак додавання синусоїдальних величин справа складна, особливо, якщо треба скласти не два, а більше число рівнянь. Тут приходить на допомогу та обставина, що змінна синусоїдальна величина може бути однозначно представлена обертовим вектором, довжина якого дорівнює амплітуді, а початкове положення визначається кутом ψ, а обертання вектора повинне відбуватися з кутовою швидкістю ω.

Рис. 4.2 Рис. 4.3

На рис. 3 представлений вектор, що відповідає рівнянню u₁=U_М1sin(ωt+ψ₁). Вектор має довжину U_М1 і в початковому положенні спрямований під кутом ψ₁ до осі абсцис. Якщо обертати цей вектор з кутовою швидкістю ω, то проекція цього вектора на вісь ординат буде давати миттєві значення напруги. Інакше кажучи, значення, обумовлені за допомогою проекції вектора і рівняння, будуть однаковими. На рис. 3 показано, що через час t (вектор повернеться на кут a = ωt, тоді проекція його на вісь ординат дасть відрізок 0а. Неважко довести, що 0а=U_М1sin(ωt+ψ₁), тобто 0a=u₁.

Так як операції проводяться з коливаннями, що мають однакову кутову частоту, то усі вектори, що замінюють рівняння, повинні обертатися з однієї і тією ж кутовою швидкістю і, отже, їхнє взаємне розташування не міняється. Завдяки цьому відпадає необхідність обертання векторів; їх зображують при t=0.

Рис. 4.4 Рис.4.5

Так як вектори заміняють синусоїдальні величини, то додавання або віднімання цих величин можна замінити додаванням або відніманням векторів. Для нашого прикладу з двома генераторами (рис. 2) рівняння напруги u₁=U_М1 sin(ωt+ψ₁) і u₂=U_М2 sin(ωt+ψ₂) представлені на рис. 4 векторами U_М1 і U_М2. Виконавши додавання цих векторів, одержимо вектор U_М, що дасть можливість написати рівняння сумарної напруги: u=U_М sin(ωt+ψ). (При побудові умовно прийнято, що U_М2>U_М1 і ψ₂ >ψ₁).

Додавання (або віднімання) векторів дає правильний результат на підставі теореми, яка говорить, що проекція суми дорівнює сумі проекцій, тобто 0c=0а+ 0b або u=u₁+ u₂.

Приклад. Дані: рівняння синусоїдальних струмів:

i₁= 2sin(ωt – 45⁰), i₂= 3sin(ωt – 60⁰). Написати рівняння сумарного струму i=i₁+ i₂.

Розв’язування. З даних рівнянь знаходимо: I_M1=2A; ψ₁= –45⁰; I_M2=3A; ψ₂ = –60⁰. За цими даними будуємо вектори (рис. 5). За результатами побудови можна написати рівняння сумарного струму: i=i_М sin(ωt+ψ)=3,15 sin(ωt+22⁰).

Таким чином, можна зробити наступні висновки:

1. Змінна синусоїдальна величина може бути однозначно представлена вектором. Довжина вектора дорівнює амплітуді, кут нахилу дорівнює початковому фазовому куту.

2. Додавання (і віднімання) синусоїдальних величин можна замінити додаванням (і відніманням) векторів.

Однак, крім додавання і віднімання, синусоїдальні величини доводиться множити й ділити. І тут на допомогу приходять КЧ.

В електротехніці, на відміну від математики, уявна одиниця позначається буквою j. Якщо є комплексне число А=а+ jb, то його можна представити вектором (рис. 6). На цьому малюнку |А|= – модуль комплексного числа; α=arctg b/a – аргумент комплексного числа.

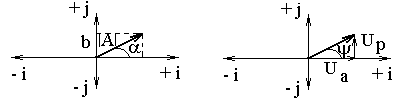
Рис. 4.6. Рис.4.7

Якщо змінна синусоїдальна величина може бути представлена вектором, а визначеному вектору відповідає визначене комплексне число, то змінна синусоїдальна величина може бути представлена комплексним числом .

Розглянемо, як виражаються різні величини комплексними числами.

1. Напруга і струм. Дано рівняння u=U_М sin (ωt + ψ). Вектор, що відповідає цьому рівнянню, представлений на рис. 7. В електротехніці за довжину вектора береться не максимальне, а діюче значення. Воно позначається великою буквою U без індексу й обчислюється шляхом ділення максимального U_М значення на . На рис. 7 показані дві проекції цього вектора: на вісь дійсних чисел – U_а (активна складова напруги) і на вісь уявних чисел – U_р (реактивна складова напруги).

Синусоїдальна величина, яка виражена комплексним числом, називається комплексом і позначається прописною буквою з крапкою нагорі – .

Відповідно до рис. 7 можна написати комплекс напруги в трьох формах:

1) алгебрична форма – =U_a+ jU_р;

2) тригонометрична форма – =U (соs ψ+ j sin ψ);

3) показникова форма – =Ue ^jω.

Таким чином, у комплексі напруги модуль дорівнює діючому значенню, а аргумент – початковому фазовому куту. Крім того, активна складова напруги дорівнює дійсній частині комплексу напруги, а реактивна – уявній частині.

Аналогічно для струму: i=I_м sin (ωt+ψ); I= I_м/; İ=I_a+ jI_p; İ=I(соs ψ+ j sin ψ); İ= Ie ^jω.

Приклад 1. Дано: i=2sin (314t – 60°). Виразити струм комплексним числом.

Розв’язання. I_М=2А; ψ= –60°; I=I_М /=2 /=1,41А.

Найпростіше написати комплекс струму в показовій формі:

=1,41e^-j60°. Перехід в алгебричну форму здійснюється через тригонометричну:

I=1,41 [соs(–60°)+jsin(–60°)]=1,41(0,5–j0,866)=0,705–j1,24, звідки I_a=0,705А, I_р= –1,24А.

Приклад 2. Дано: струм у комплексній формі İ=3–j4. Написати рівняння струму.

Розв’язання. Для того щоб написати рівняння, треба знати амплітуду і початковий фазовий кут. Тому треба знайти модуль – діюче значення й аргумент – початковий фазовий кут заданого комплексу струму:; ;

I= I_М / =5 =7,07A; i=I_М sin (ωt+ψ)=7,07(ωt-53°).

Для стандартної кутової частоти замість w можна написати 314 рад/с.

2. Опір і провідність. Дано коло (рис. 8): r – активний опір, наприклад, лампа розжарювання; Х_L – індуктивний опір, наприклад котушка; z – загальний опір кола, названий повним.

Опори r, Х_L, z утворять прямокутний трикутник опору (рис. 9). Кут (j називається кутом зсуву фаз. Однак відрізок z може бути виражений комплексним числом, якщо вважати, що відрізок r відкладається по осі дійсних чисел, а відрізок Х_L – по осі уявних чисел.

Рис.4.8 Рис.4.9 Рис.4.10

Опір у комплексній формі позначається буквою Z. Для кола на рис. 9 комплекс опору запишеться так:

1) Z=r+j Х_L – алгебрична форма;

2) Z= z (соs j + j sin j) – тригонометрична форма;

3) Z = ze ^jφ – показникова форма.

Модуль z=, аргумент =arctgX_L/r. Таким чином, у комплексі опору модуль дорівнює повному опору, а аргумент – зсуву фаз.

Рис.4. 11

Аналогічно для кола, представленого на рис. 10, де Хс – ємнісний опір, наприклад, конденсатор. Трикутник опорів зображений на рис. 11. Комплекс опору для цього кола:

Z=r – j Хс; Z=z (соs j +j sin j); Z = ze ^{- jφ}.

Модуль z= аргумент =arctg(-X_C /r).

Провідність – це величина, обернена до опору. Y=1/Z – комплекс провідності. Для знаходження Y скористаємося виразом для комплексу опору: Z=r+ jX_L (див. рис. 8):

Позначивши r/z²=g; z²=b, одержимо Y=g– jb, де g – активна провідність; b – реактивна провідність. У показниковій формі Y=y e ^{- jω}, де b = ; y – повна провідність; =arctg(b /g).

Аналогічно для кола на рис. 10: Y=g+j b; Y=y e ^{- jφ},

де b_с – реактивна провідність; у=; =аrсtg(/g).

3. Потужність. Комплекс потужності отримаємо, якщо комплекс напруги помножимо на спряжений комплекс струму:

=U, де – комплекс потужності; – спряжений комплекс струму.

Після множення одержимо комплексне число, у якого дійсна частина дорівнює активній потужності, а уявна частина – реактивній потужності: =P + j, де Р – активна потужність; Q – реактивна потужність.

Приклад. Дано: U=43,5+ j55,6; I=10,4+ j9,35. Визначити активну Р і реактивну Q потужності.

Розв’язання. Переводимо комплекси напруги і струму в показову форму. Для цього знаходимо модуль і аргумент струму і напруги:

; 70,7e^j52°

=14e ^j42°.

Далі визначаємо спряжений комплекс струму:

=14e ^{– j42°}; =70,7e ^j52°14e ^{– j42°}=99014e ^j10°=990(соs 10°+ j sin 10)= = 990(0,984+j0,173)=975+j171.

Знаходимо активну й реактивну потужності: P=975 Вт; Q=171 вар.