
- •Робочий зошит для проведення практичних занять з дисципліни «Вища математика»
- •5.03050702 «Комерційна діяльність»
- •Практична робота № 1
- •Теоретичні відомості про перетворення графіків тригонометричних функцій.
- •Методичні рекомендації до виконання роботи.
- •Теоретичні відомості про графіки обернених тригонометричних функцій.
- •Методичні рекомендації до виконання роботи
- •Питання для самоперевірки вмінь:
- •Тема2. Комплексні числа практична робота № 2
- •Інструкційні картки;
- •Теоретичні відомості про комплексні числа.
- •Питання для самоперевірки знань, умінь.
- •Тема 3. Елементи лінійної алгебри практична робота № 3
- •Інструкційні картки;
- •Теоретичні відомості про матричний спосіб розв’язування систем лінійних рівнянь.
- •Питання для самоперевірки знань, умінь
- •Тема 4. Елементи векторної алгебри практична робота № 4
- •Інструкційні картки;
- •Теоретичні відомості про скалярний, векторний та мішаний добутки.
- •Питання для самоперевірки знань, вмінь:
- •Тема 5. Аналітична геометрія практична робота № 5
- •Інструкційні картки;
- •Теоретичні відомості про кути між прямими, взаємне розташування прямих в просторі.
- •Питання для самоперевірки знань, вмінь:
- •Практична робота № 6
- •Інструкційні картки;
- •Приклади задач;
- •Теоретичні відомості про коло.
- •Теоретичні відомості про еліпс.
- •Теоретичні відомості про гіперболу
- •Теоретичні відомості про параболу
- •Питання для самоперевірки знань, умінь.
- •Тема 6. Системи лінійних нерівностей і лінійне програмування практична робота № 7
- •Інструкційні картки;
- •Приклади задач;
- •Теоретичні відомості про транспортну задачу.
- •Питання для самоконтролю знань, умінь.
- •Тема 7. Диференціальне числення функції однієї змінної. Практична робота № 8
- •Інструкційні картки;
- •Приклади задач;
- •Теоретичні відомості про правила диференціювання.
- •Теоретичні відомості про диференціал функції.
- •Питання для самоконтролю знань, умінь.
- •Практична робота №9
- •Інструкційні картки;
- •Приклади задач;
- •Теоретичні відомості про найбільше і найменше значення функції на проміжку
- •Теоретичні відомості про екстремум функції.
- •Теоретичні відомості про застосування похідної.
- •Питання для самоконтролю знань, умінь.
- •Тема 8. Диференціальне числення функції багатьох змінних практична робота №10
- •Інструкційні картки;
- •Приклади задач;
- •Теоретичні відомості про правила диференціювання.
- •Частинні похідні.
- •Питання для самоконтролю знань, умінь.
- •Тема 9. Інтегральне числення. Практична робота № 11
- •Інструкційні картки
- •Приклади задач
- •Теоретичні відомості про правила інтегрування та застосування визначеного інтегралу.
- •1. Визначений інтеграл та методи його обчислення
- •2. Застосування визначеного інтегралу до обчислення шляху за відомим законом зміни швидкості.
- •Питання для самоконтролю знань, умінь.
- •Тема 10. Диференціальні рівняння практична робота № 12
- •Інструкційні картки
- •Приклади задач
- •Теоретичні відомості про диференціальні рівняння другого порядку зі сталими коефіцієнтами.
- •Питання для самоконтролю знань, умінь.
- •Література
- •Рецензія
Питання для самоперевірки вмінь:
-
Як називається графік функції
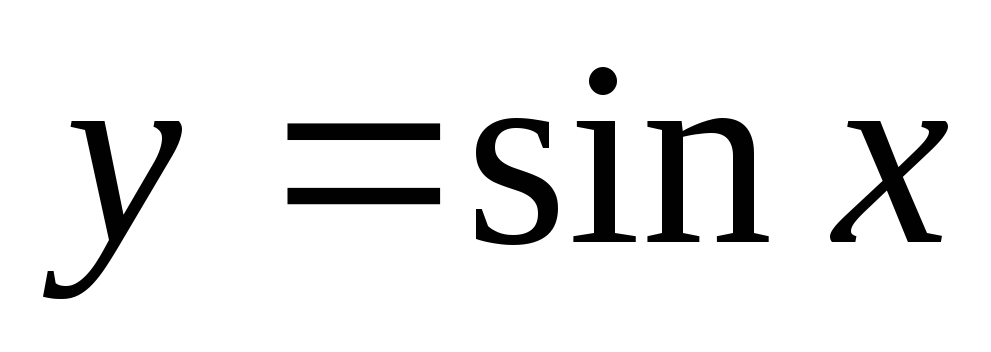 ?
?
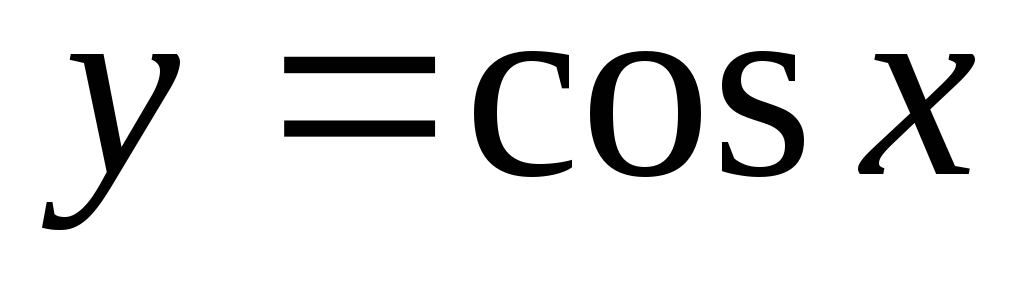 ?
?
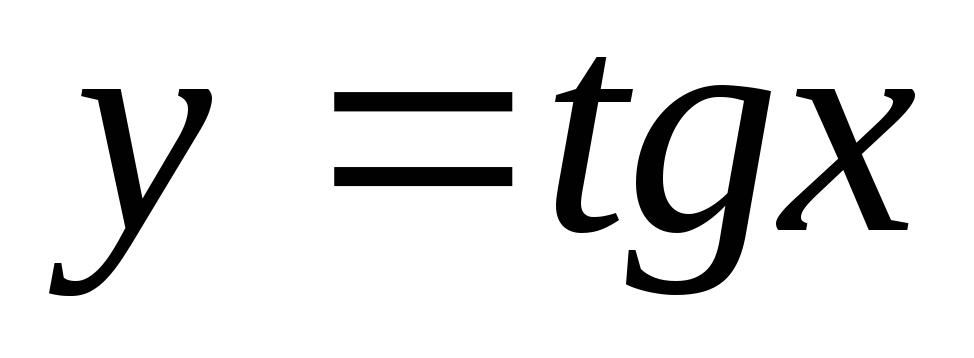 ?
?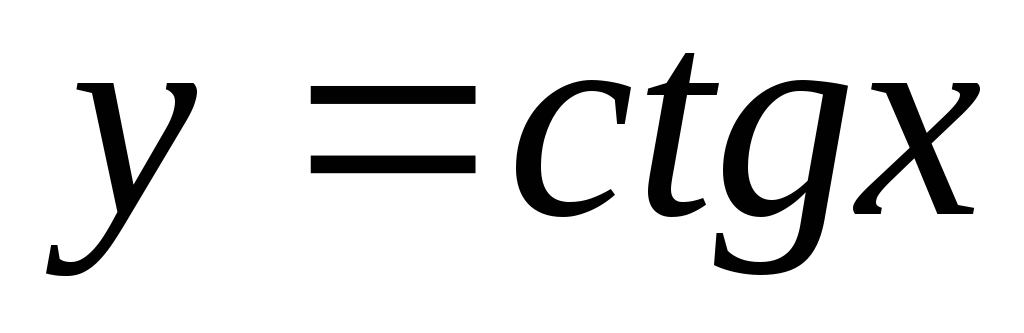 ?
? -
Пояснити побудову графіка функції
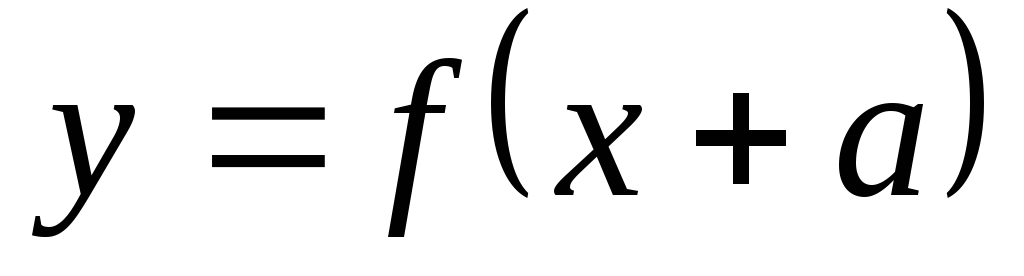
-
Пояснити побудову графіка функції
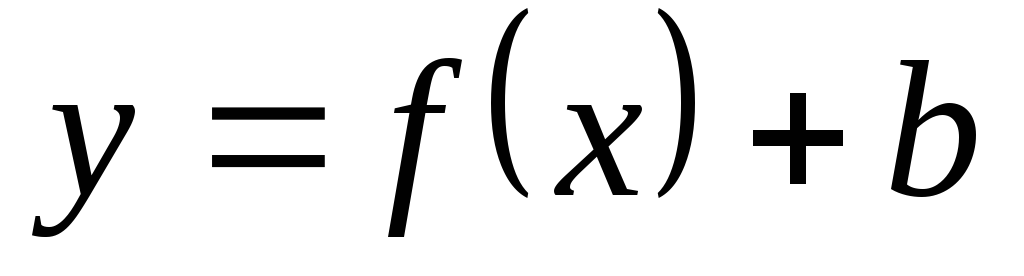
-
Пояснити побудову графіка функції
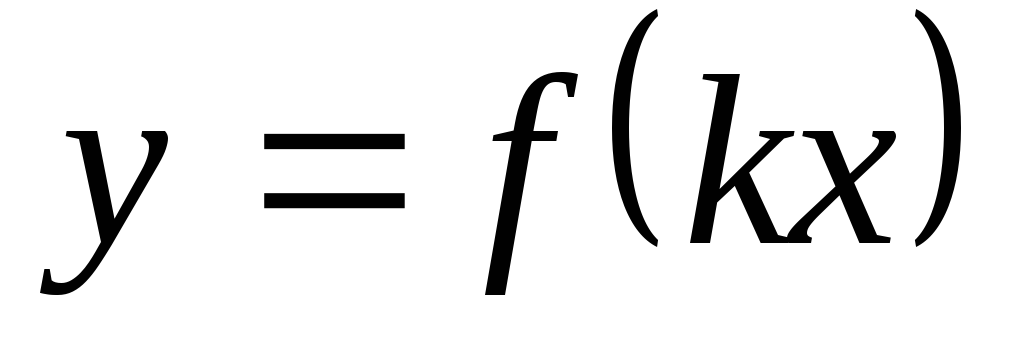
-
Пояснити побудову графіка функції
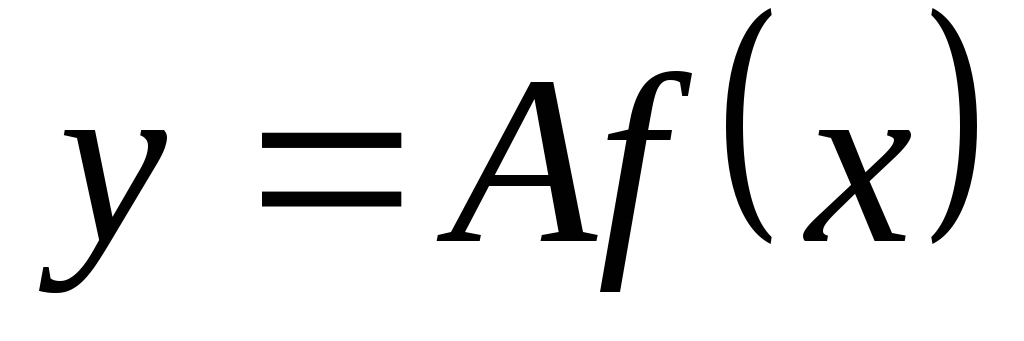
-
Пояснити побудову графіка функції

-
Пояснити побудову графіка функції
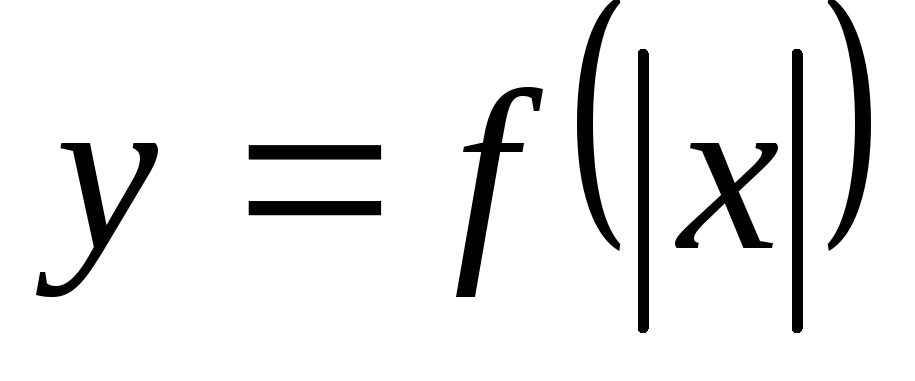
-
Необхідна умова існування функції оберненої до даної.
-
Які функції називаються взаємно оберненими?
-
Які особливості зображення двох взаємно обернених функцій в одній системі координат?
Перевірив викладач ___________ Оцінка___________Дата ______________
Тема2. Комплексні числа практична робота № 2
Тема. Показникова форма комплексного числа. Перехід від
алгебраїчної форми до показникової. Дії над комплексними
числами, заданими в тригонометричній та показниковій формах.
Мета роботи: навчитись переходити від алгебраїчної форми комплексного числа до показникової та тригонометричної, виконувати дії над комплексними числами, заданими в показниковій та тригонометричній формах.
Наочне забезпечення та обладнання:
-
Інструкційні картки;
-
Індивідуальні завдання;
-
Роздатковий матеріал: опорні конспекти “Комплексні числа та дії над ними”.
Теоретичні відомості про комплексні числа.
Тригонометрична форма комплексного числа.
Модулем
комплексного числа
![]() називається довжина вектора
називається довжина вектора
![]() ,
яку можна знайти за формулою
,
яку можна знайти за формулою
![]() .
.
Аргументом
комплексного числа називається кут
![]() ,
який утворює вектор
,
який утворює вектор
![]() з додатнім напрямком осі абсцис.
з додатнім напрямком осі абсцис.
Величину
кута
![]() можна знайти з системи
можна знайти з системи


![]() -
тригонометрична
форма комплексного числа.
-
тригонометрична
форма комплексного числа.
Дії над комплексними числами, заданими в тригонометричній формі
Нехай дано два комплексних числа
![]()
![]() .
.
Добуток
![]()
![]() .
.
Частка
![]()
![]() .
.
Степінь
![]()
![]() .
.
Корінь
n-го
степеня
![]() ,
де k=0,1,2,3,…,
(n-1).
,
де k=0,1,2,3,…,
(n-1).
Задача №1. Дано комплексні числа:
![]()
![]() .
Знайти:
.
Знайти:
а)
![]() =
=
б)
![]() =
=
в)
![]() =
=
г)
![]() =
=
Показникова форма комплексного числа.
![]() -
формула
Ейлера. Тоді показникова форма комплексного
числа буде:
-
формула
Ейлера. Тоді показникова форма комплексного
числа буде:
![]()
Задача №2. Записати комплексне число в показниковій та тригонометричній формах:
а)
![]()
б)
![]()
в)
![]()
Задача №3. Записати комплексне число в алгебраїчні та показниковій формах:
а)
![]()
б)
![]()
Задача №4. Записати комплексні числа в алгебраїчній і тригонометричній формах:
а)
![]()
б)
![]()
Задача №5. Виконати дії і записати результат в показниковій формі:
а)
![]() =
=
б)
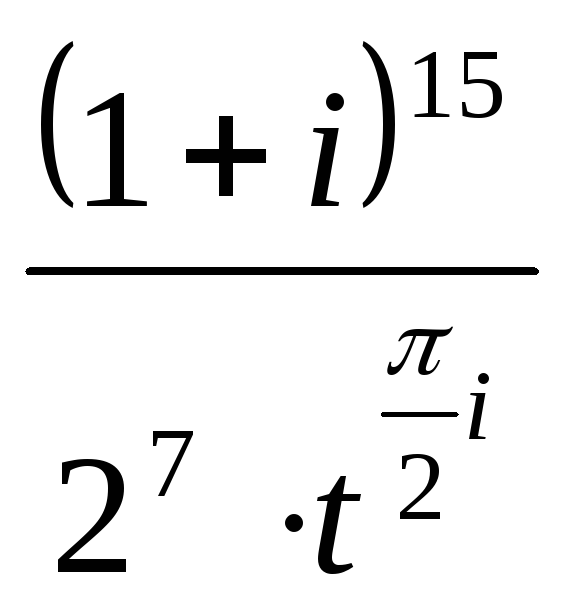 =
=
Питання для самоперевірки знань, умінь.
-
Дайте означення уявної одиниці.
-
Як обчислюють степені уявної одиниці?
-
Дайте означення комплексного числа.
-
Які комплексні числа називаються рівними?
-
Які комплексні числа називаються комплексно – спряженими?
-
Дії над комплексними числами, що задані в алгебраїчній формі.
-
Геометрична інтерпретація комплексних чисел.
-
Модуль і аргумент комплексного числа.
-
Тригонометрична форма комплексного числа.
-
Показникова форма комплексного числа.
-
Дії над комплексними числами, заданими у тригонометричній формі (показниковій формі).
-
Скільки значень має корінь n – го степеня з комплексного числа.
-
Розв’язування квадратних рівнянь з від’ємним дискримінантом.
-
Які корені і скільки коренів має квадратне рівняння з від’ємним дискримінантом?
Перевірив викладач ___________ Оцінка___________Дата ______________
