Питання для самоконтролю знань, умінь.

1. Які точки називаються критичними ?

2. Правило знаходження найбільшого та найменшого значення функції.

3. Які точки називаються точками максимуму і точками мінімуму ?

4. Перше правило відшукання екстремуму функції.

5. Друге правило відшукання екстремуму функції.

6. Фізичний зміст похідної.

7. Геометричний зміст похідної. Рівняння дотичної до графіка функції.

Перевірив викладач_________________ Оцінка _________Дата________

Тема 8. Диференціальне числення функції багатьох змінних практична робота №10

Тема. Основні поняття та означення функції багатьох змінних. Частинні похідні. Екстремуми функції багатьох змінних. Необхідна умова існування точок екстремуму.

Мета роботи: засвоїти означення функції двох змінних, правила дослідження на екстремум; навчитись проводити дослідження функції двох змінних на екстремум; застосовувати здобуті навички для розв’язування прикладних задач економічного змісту.

Наочне забезпечення та обладнання:

1. Інструкційні картки;

2. Приклади задач;

3. Роздаткові матеріали: опорні конспекти “ Диференціювання функцій багатьох змінних”

4. Обчислювальні засоби: калькулятор.

Теоретичні відомості про правила диференціювання.

Функцією двох змінних , називається функція, яка кожній парі чисел ставить у відповідність деяке число .

Аналогічно означається функція трьох і більше невідомих.

Частинні похідні.

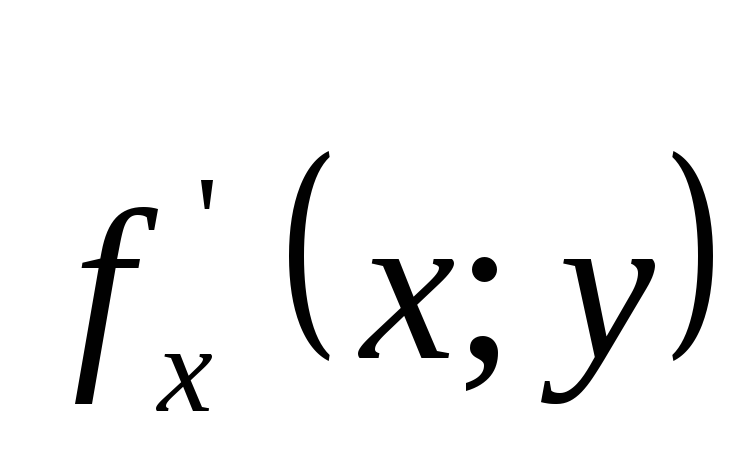- це похідна по функції при фіксованому

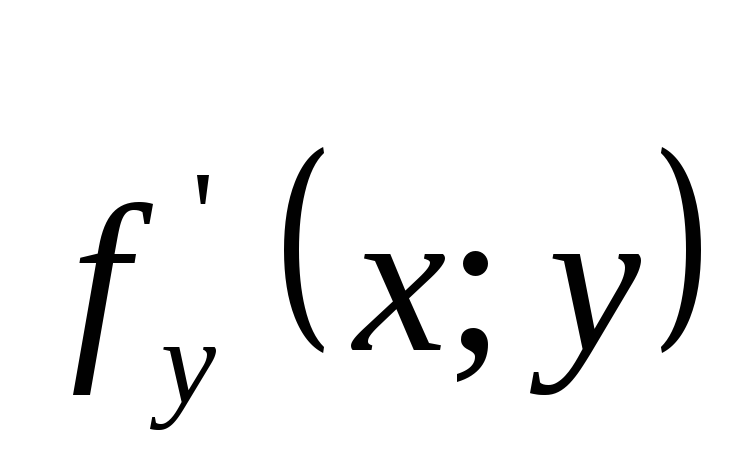- це похідна по функції при фіксованому .

Частинні похідні функції знаходять за звичайними правилами диференціювання; потрібно тільки при диференціюванні по змінну вважати сталою, а при диференціюванні по вважати сталою.

Якщо , то ; - частинні похідні першого порядку.

- частина похідної другого порядку.

- мішані похідні другого порядку.

Якщо мішані похідні неперервні, то вони рівні.

Задача №1. Знайти частинні похідні першого і другого порядків від заданих функцій:

а) z = 8e- 3xy+ 7x – 3

б) z = xsiny + 8xy- 7x

Дослідження функцій z = f (x,y) на екстремум

При дослідженні функцій z = f (x,y) на екстремум (при умові, що вона двічі диференційована) користуються правилом:

1.Знаходяться частинні похідні першого порядку функції z = f (x,y) і розв’язують систему рівнянь:

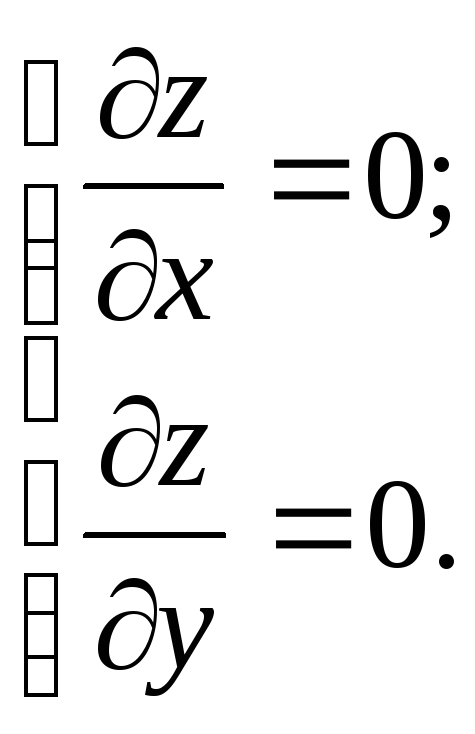
Точки, в яких частинні похідні дорівнюють нулю, називаються стаціонарними точками. Нехай одна з них

2. Знаходять частинні похідні другого порядку та мішані функції z = f (x,y) і обчислюють їх значення в точці

Позначимо ; ; .

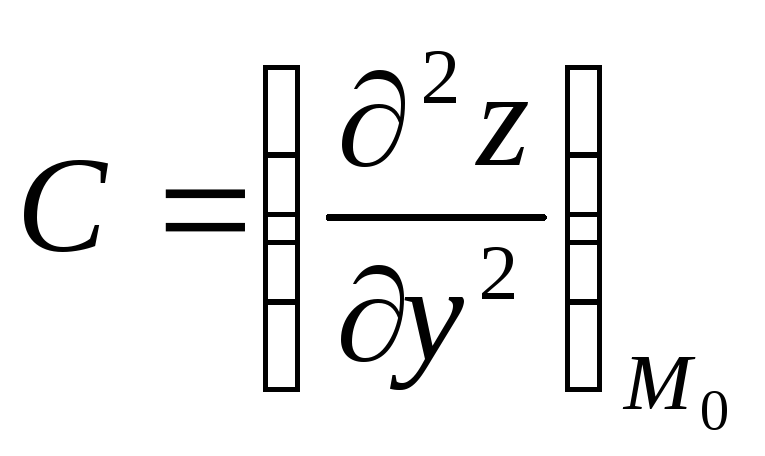3. Обчислюють визначник

.

Якщо виявляється , що то функція z = f (x,y) в точці має максимум при і мінімум при . Якщо ж то в точці екстремуму немає. Нарешті, якщо то питання про екстремум в цій точці залишається відкритим і вимагає додаткового дослідження.

Задача 2. Знайти екстремум заданої функції

а)

б)

Задача 3. Мале підприємство виробляє товари А і В. Загальні щоденні витрати V (в гривнях) на виробництво x одиниць товару А та y одиниць товару В відомі: . Визначити кількість одиниць товарів А і В, яку потрібно виробляти, щоб загальні витрати підприємства були мінімальними.