2. Представлення чисел і елементи двійкової арифметики в цифрових пристроях
2.1 Позиційні системи числення
Дані, які обробляються в мікропроцесорних пристроях, є числами. Одне і те ж число можна виразити різними комбінаціями цифр і буквених символів. Конкретний вид такої комбінації залежить від вибраної системи числення.
Всяке ціле число N можна представити у такий спосіб:
де число h- основа системи; а- розрядні коефіцієнти; n- число розрядів числа N. Для формального запису числа N використовують тільки розрядні коефіцієнти, тобто
Подібний запис характерний для позиційної системи числення. Позиційні системи розрізняють в залежності від їх основи. Найчастіше в цифрових мікропроцесорних засобах застосовують двійкову та шістнадцяткову систему числення.
Двійкова система
Для неї h=2, і алфавіт системи утворює дві цифри: 0 і 1. Таким чином n-розрядне число N в цій системі числення має вид
де а може приймати тільки два значення: або 0, або 1. Наприклад, число 21(10) в двійковій системі має такий еквівалент 10101(2). Алгоритми перетворення десяткового числа у двійкове і навпаки приведені відповідно на рисунку 2.1 і в таблиці 2.1.
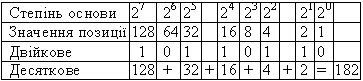
Таблиця 2.1 – Зворотне двійково-десяткове перетворення числа 10110110(2)
1
55(10):2=77
залишок 1мл.розряд
77(10):2=38 залишок 1
38(10):2=19 залишок 0
19(10):2 = 9 залишок 1
9(10) : 2 = 4 залишок 1
4(10) : 2 = 2 залишок 0
2(10) : 2 = 1 залишок 0
1(10) : 2 = 0 залишок 1ст.біт
155(10)= 1 0 0 1 1 0 1 1(2)
Рисунок 2.1 – Алгоритм прямого двійково-десяткового
перетворення
Шістнадцяткова система
Дана система числення забезпечує компактний запис великих чисел, але вона не використовується для безпосередніх обчислень. Основа системи h=16, а її алфавіт складається із десяти цифр від 0 до 9 і шести латинських букв (A, B, C, D, E, F), при чому вони є відповідниками чисел 10, 11, 12, 13, 14, 15 десяткової системи числення. В таблиці 2.2 приведені еквіваленти різних систем числення:
Таблиця 2.2 – Десяткові, шістнадцяткові і двійкові еквіваленти
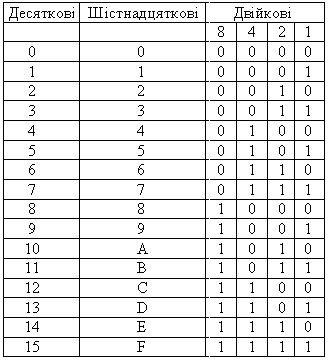
Перетворення десяткових цілих та дробових чисел в шістнадцяткові показане на рисунку 2.2:
1
5797(10):16=987
залишок 5(10)=5(16)мл.розряд
987(10):16=61 залишок 11(10)=B(16)
61(10):16=3 залишок 13(10)=D(16)
3(10):16=0 залишок 3(10)=3(16) ст.розряд
15797(10)=3DB5(16)
а)
0
,216(10)
16
ст.розряд 1 296
2 16
3,456
16
2 736
4 56
7,296
16
1 776
2 96
м
л.розряд
4,736
0, 3 7 4 (16)0,216(10)
Рисунок 2.2 – Перетворення десяткових чисел в шістнадцяткові еквіваленти: а) –цілі числа; б) –дробові числа.
Таким чином, алгоритм переводу цілого числа з однієї позиційної системи в іншу такий: число ділиться на основу нової системи числення h і визначається залишок; частка знову ділиться не h і знову визначається залишок; так продовжується до тих пір, доки частка не буде меншою за h ; після цього виписується остання частка і всі залишки – це і буде еквівалент числа з основою h.
Алгоритм переводу дробового числа із однієї позиційної системи в іншу полягає в наступному: вихідне число множиться на основу нової системи h, далі дробова частина добутку знову множиться на h; так повторюють стільки раз, скільки розрядів числа в новій системі числення потрібно одержати. Тоді виписують цілі частини всіх добутків – це і буде еквівалент числа з основою h.
Перетворення шістнадцяткового числа в десяткове здійснюється за відомою схемою:
2C6(16)=2*163+C*162+6*161+E*160=2*4096+12*256+6*16+14*1=
=11374(10)
Перевід двійкового числа у шістнадцяткову систему передбачає розбивання вихідного числа на тетради, починаючи з молодшого біта, і заміни кожної тетради еквівалентною цифрою або буквою шістнадцяткового алфавіту (якщо при утворенні останньої тетради не залишилось необхідної кількості двійкових цифр, то зліва добавляють нулі).
Приклад:
Перевід двійкового числа з шіснадцяткової системи у двійкову здійснюється у зворотньому порядку.
Мікропроцесори, крім операцій з двійковими числами, можуть оперувати з двійково-десятковими числами. В цьому випадку числа представляються спеціальним двійково-десятковим кодом (BDC). В таблиці 2.2 приведені еквіваленти десяткових чисел від 0 до 9 (розглядати тільки відповідну частину таблиці) та їх BDC – коди в системі 8421. BDC – еквівалент десяткового числа одержують за такою схемою: кожну десяткову цифру перетворюють прямо в свій двійково-десятковий еквівалент із 4 бітів.
Приклад:
Зворотне перетворення BDC – числа в десятковий еквівалент полягає в заміні групи із чотирьох бітів її десятковим відповідником.