2.1.2 Динамічні системи
Динамічною
називається
інерційна (нестатична) система, в якої
визначено функції переходу станів
і
вихідної реакції
.
Стаціонарними динамічними називають клас динамічних систем, стан та структура яких не залежить від того, в який момент часу розглядатиметься вплив. Про них говорять, що ці системи є інваріантні щодо часового зсуву:
, (2.2)
тобто
для кожного моменту часу
можна визначити оператор зсуву часу
,
такий,
що реакція системи на вхідний вплив у
момент часу
залежить
лише від різниці між часом його початку
і поточним часом, а не від поточного
часу, при цьому
.
Для
стаціонарної системи
,
де
,
,
впливи
і реакції є стаціонарними, якщо
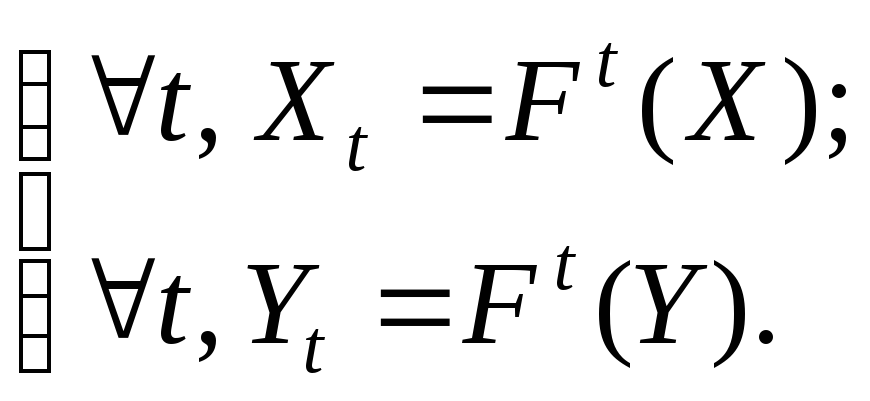(2.3)
Важливою властивістю стаціонарних (інваріантних у часі) систем є те, що функцію переходу стану для будь-якого моменту часу можна отримати як результат застосування оператора зсуву до початкової реакції системи.
Адекватним описом математичної моделі динамічної системи є диференційне рівняння
, (2.4)
де
–
множина станів системи;
– множина
збурюючих впливів.
Перша
похідна
,
яка
є не що інше, як швидкість зміни станів
системи, може дорівнювати нулю, що
відповідає стану спокою системи. Вона
може дорівнювати від'ємній або додатній
величині, бо це рівняння може мати змінну
праву частину:
,
. (2.5)
При
система
поводить себе збуджено, нестатично, при
вона
повертається в стан спокою і її поведінка
є сталою:
. (2.6)
Очевидно,
що при
динамічна
система стає статичною, при відході від
до 0 інерційність зростає, при
система стає нерухомою, перебуває в
стані спокою.
2.2 Властивості систем
2.2.1 Цілісність
Цілісність є однією з найхарактерніших властивостей усіх систем, яка полягає у виникненні нових інтегральних якостей, невластивих для утворюючих систему компонентів. Так, властивості системи зв'язку щодо забезпечення стійкості та інших показників не є простою сумою властивостей елементів, з яких вона складається. І у систем живої природи (мурашників, термітників, бджолиних сімей, а також спілок людей, націй тощо) системні властивості також не є простою сумою властивостей індивідуумів.
Властивості цілісності виявляються в системі з двох основних сторін:
-
властивості системи як цілого не зводяться до суми властивостей елементів або частин;
-
властивості системи як цілого залежать від властивостей елементів та частин: модифікація однієї частини спричиняє модифікації в усіх інших частинах і у всій системі.
Суттєвим виявом властивості цілісності є нові взаємовідносини системи як цілого з оточенням, відмінні від взаємодії окремих елементів з цим оточенням. Властивість цілісності пов'язана з метою, для виконання якої система призначена.
Системи можуть мати альтернативну цілісності властивість – фізичну адитивність, незалежність. Властивість фізичної адитивності (незалежності елементів) виявляється у системи, яка немовби розпалася на незалежні елементи. Очевидно, що у випадку, коли всі елементи стають незалежними, говорити про систему немає сенсу. Таким чином, будь-яка система перебуває між двома крайніми станами: абсолютною цілісністю, що досягається при максимальному зв'язку між елементами, і абсолютною адитивністю, коли ці зв'язки відсутні (рис. 2.2).
Інколи, розглядаючи еволюцію систем, вводять такі поняття, як факторизація (прагнення системи до стану з усе більш незалежними елементами) і прогресуюча систематизація, цілісність (прагнення системи до більшої цілісності, до зростання залежності між елементами).
Рисунок 2.2 – Цілісність та адитивність систем