Д.1.6 Способи завдання бінарних відношень

Можна привести кілька різних способів завдання бінарних відношень (переваги кожного зі способів визначаються властивостями множини ).

Перший, очевидний спосіб полягає в безпосередньому перерахуванні таких пар. Зрозуміло, що він прийнятний лише у випадку скінченої множини .

Другий спосіб завдання відношення на скінченій множині – матричний. Відношення задається, у загальному випадку, прямокутною матрицею. Для цього всі елементи множини нумеруються, а елементи матриці відношення визначається за формулою

для всіх ,.

Наприклад, у випадку бінарного відношення – «строго більше» на множині отримаємо наступну матрицю:

При цьому .

Третій спосіб – завдання відношення у вигляді двучасткового графу. Вершинам графа ставляться у відповідність (пронумеровані) елементи множини , і якщо , то від вершини , проводять спрямовану дугу до вершини , якщо , то дуга відсутня. Для розглянутого вище відношення, такий граф буде мати вигляд

Д.1.7 Відношення еквівалентності, порядку й домінування

Відношення можна віднести до того або іншого типу, якщо встановити, які властивості воно має. Розглянемо основні властивості бінарних відношень:

• рефлексивність ;

• антирефлексивність ;

• симетричність ;

• асиметричність ;

• антисиметричність ;

• транзитивність ;

Розглянемо деякі, найбільш важливі з практичної точки зору, типи відношень.

Відношенням еквівалентності (позначається значками “=” або “”) називається відношення, що задовольняє наступним властивостями:

• рефлексивності ;

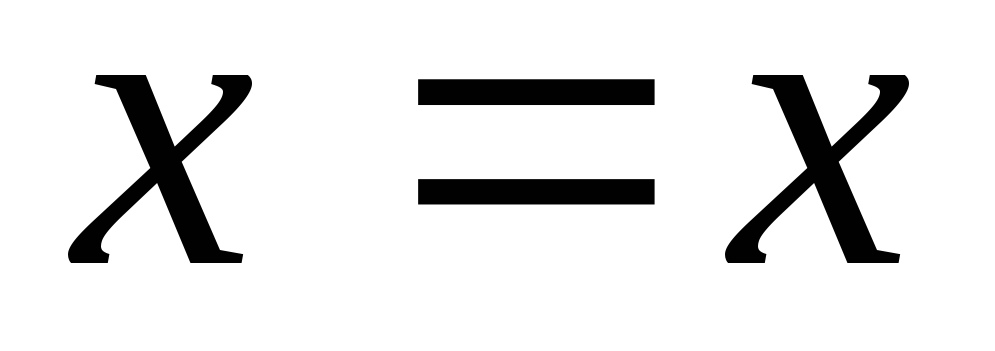• симетричності ;

• транзитивності .

Приклади відношень еквівалентності: "бути парним" – на множині натуральних чисел; "бути однокурсниками" – на множині студентів даного навчального закладу; відношення подібності на множині трикутників і т.д.

Завдання відношення еквівалентності рівносильне розбиттю множини на непересічні класи (такі, що ) еквівалентних елементів, а саме: тоді й тільки тоді, коли , тобто елементи належать одному класу еквівалентності.

Відношенням нестрогого порядку (використовуються позначення:, ) називається відношення, що має наступні властивості:

• рефлексивності ,

• антисиметричності ,

• транзитивності .

Відношенням строгого порядку (використовуються позначення , ) називається відношення, що має наступні властивості:

• антирефлексивності хибне;

• асиметричності та взаємновиключаєтся;

• транзитивності з .

Відношенням домінування називається відношення, що задовольняє двом властивостям: антирефлексивності й асиметричності. Говорять, що " домінує " (позначається ), коли в якомусь сенсі перевершує . Це відношення, як правило, використовується для опису адміністративних, управлінських, а в загальному випадку ієрархічних систем.

Д.1.8 Відображення. Функції

У класичному математичному аналізі поняття функції вводиться в такий спосіб. Нехай – деяка множина на числовій прямій. Говорять так: функція визначена на множині, якщо кожному числу поставлене у відповідність певне число . При цьому називають областю визначення даної функції, а множину всіх значень, що приймає ця функція, – її областю значень.

Якщо розглядати множини довільної природи, то поняття функції необхідно узагальнити й на цей випадок. Нехай задано дві довільні множини та .

Відображенням (однозначним) множини на множину називається закон, за яким кожному елементу ставиться у відповідність певний елемент (не виключається, що може збігатися з ). Таке співвідношення між та записується у вигляді: , , , або найчастіше

.

При цьому називається областю визначення відображення, а – областю його значень.

Відображення породжує множину

,

яке називається графіком відображення.

Відображення і називаються рівними, якщо їх області визначення збігаються і , тобто збігаються й області значень.

Відображення називається постійним, якщо

.

Нехай задано три множини , та . Якщо визначені відображення

і ,

то існує відображення

,

яке визначається рівністю

.

Це відображення називається композицією відображень і позначається

.

Відображення називають ще складним відображенням. Відображення називається багатозначним, якщо деякому відповідає підмножина , що складається більш ніж з одного елемента.

Нехай , тоді йому відповідає елемент такий, що . Елемент b називається образом при відображенні . Сукупність усіх тих елементів , образом яких є даний елемент , називається прообразом, або, точніше, повним прообразом елемента і позначається .

Нехай ; множина називається образом підмножини й позначається . У свою чергу для кожної множини визначається її (повний) прообраз , а саме: є сукупність усіх тих елементів з , образи яких належать .

Розглянемо тільки деякі самі загальні властивості відображень.

Якщо відображення таке, що , тобто область визначення співпадає з множиною Y, то його називають сюр'єктивним відображенням або сюр'єкцією. Якщо для будь-яких двох різних елементів їх образи та також різні, то таке відображення називається ин'єктивним або ін'єкцією. Відображення, яке одночасно є сюр'єкцією та ін'єкцією, називається бієкцією або взаємно однозначним відображенням між та .