3.3 Приклад застосування методів загальної теорії систем для проектування комутаційних систем зв’язку

Системи зв’язку мають скінчену кількість каналів для обслуговування викликів абонентів. При надходженні в систему чергового виклику система зв’язку один зі своїх входів з’єднує з певним виходом за допомогою комутаційних пристроїв. Об’єднання декількох комутаційних пристроїв в цілісну схему зв’язку називають системою або схемою комутації. Розрізняють повно доступні та неповно доступні системи комутації.

У повно доступній системі комутації кожен вхід з’єднується з усіма виходами – каналами зв’язку системи. Розглянемо модель повно доступної комутаційної системи, елементами якої є комутаційні пристрої

,

причому множини входів та виходів мають наступний склад , . Нехай, для простоти система комутації має три входи та два виходи. Для того щоб створити повно доступну систему комутації необхідно скористатись операціями каскадного та паралельного з’єднання систем. Візьмемо три комутаційні пристрої , та і з’єднаємо їх паралельно за виходами

У результаті такого з’єднання отримаємо комутаційну підсистему

Функція цієї підсистеми полягає в з’єднанні входів системи з каналом зв’язку та перенаправленні навантаження на інші канали через підмножину виходів , коли канал зайнятий. Побудуємо комутаційну підсистему, що з’єднує входи з каналом . У цьому випадку будемо використовувати комутаційні пристрої, що мають по одному входу та по одному виходу, а саме , та . З’єднаємо ці комутаційні пристрої знову таки ж паралельно за виходами. У результаті отримаємо підсистему (див. рис )

,

де .

Тепер з’єднаємо підсистеми та використовуючи операцію каскадного з’єднання систем. При цьому , та .

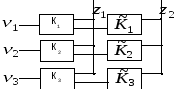
У результаті отримаємо систему . Якщо обчислити декартів добуток множин входів та виходів системи , то можна переконатись, що кожен зі входів системи комутації з’єднується з усіма її виходами:

.

У отриманій системі кортежі визначають відношення, яке можна назвати з’єднанням: вхід з’єднаний з виходом .

Використовуючи методи загальної теорії систем можна не тільки ефективно проектувати комутаційні схеми довільної складності, а й на їх підґрунті розробляти системи автоматизованого проектування комутаційних схем.

3.4 Контрольні запитання

1. Які основні способи з'єднання систем ви знаєте?

2. Сформулюйте визначення підсистеми.

3. Що таке максимальна незалежна декомпозиція системи?

4. Які основні способи декомпозиції систем ви знаєте?

4 Нечіткі системи

Намагаючись формалізувати людські знання, дослідники постійно зіштовхуються з такою проблемою. Існує клас явищ, процесів та об'єктів, для опису яких використовуються переважно якісні характеристики (мало, багато, сильний, слабкий й т.і.). Ці характеристики звичайно розмиті (нечіткі) і не можуть однозначно інтерпретуватися, однак містять важливу інформацію. Наприклад, «Однією з можливих ознак грипу є висока температура». Це дуже ускладнює, а найчастіше унеможливлює використання традиційного математичного апарату для їхнього опису та розробки формальних моделей. Не виключено, що системи з нечіткими характеристиками можна було б описати в межах класичної теорії множин. Однак виникає одна принципова перешкода, що міститься в самому визначенні множини. Для заданої множини і деякого об'єкта може виконуватися тільки одне з двох співвідношень: або , або . При цьому саму множину можна розглядати як сукупність еквівалентних елементів, еквівалентних у тому сенсі, що усі вони мають однакову властивість: належать множині . Спробуємо тепер скласти множину елементи якої – відстані що відповідають суб'єктивному поняттю «близько». У межах класичного підходу цю множину визначимо в такий спосіб. Будемо вважати, що усі відстані менші або рівні 1000 м. – це відстані які відповідають поняттю «близько». У такий спосіб . Однак, у різних людей поняттю «близько» відповідають різні граничні значення таких відстаней. Наприклад, для однієї групи людей «близько» – це відстань до 800 м., для іншої групи – до 1500 і т.д. Звідси випливає, що множин , строго кажучи, не має чіткої границі, отже, в одному випадку може належати множині , а в іншому – ні. При цьому елементи множини вже не еквівалентні між собою, тому що не можна однозначно визначити їхню належність даній множині. Крім того, з цим поняттям зв'язані ще такі його градації «дуже близько», «не дуже близько», «не далеко». Таким чином, у рамках класичної теорії множин не вдається описати подібні об'єкти, зберігши при цьому нечіткість (розпливчастість) їхніх характеристик.