4. Orthogonalité dans l’espace

4. 1 Droite et plan orthogonaux

Mots à retenir

le projeté orthogonal de A sur le plan P (ортогональная проекция точки А на плоскость Р)

la distance du point A au plan P (расстояние от точки А до плоскости Р)

le pied de la perpendiculaire (основание перпендикуляра)

Définitions

1) Deux droites perpendiculaires dans l’espace sont deux droites sécantes formant quatre angles droits.

2) On dit que deux droites de l’espace sont orthogonales lorsqu’elles sont parallèles à deux droites perpendiculaires.

Remarque Deux droites de l’espace qui sont orthogonales ne sont pas obligatoirement coplanaires (donc ne sont pas obligatoirement perpendiculaires).

Exemple :

Dans le cube ABCDEFGH ci-contre :

les droites (EH) et (FG) sont parallèles ;

les droites (GC) et (FB) sont parallèles ;

les droites (FG) et (FB) sont perpendiculaires ;

donc les droites (EH) et (GC) sont orthogonales. On note:

3) Une droite perpendiculaire à un plan est une droite orthogonale à toutes les droites de ce plan.

Propriétés :

1) Si une droite est perpendiculaire à deux droites sécantes d’un plan, elle est perpendiculaire à ce plan.

2) Si deux droites sont perpendiculaires à un même plan, elles sont parallèles.

3) Si deux droites sont parallèles, alors tout plan orthogonal à l’un est orthogonale à l’autre.

4) Deux plans orthogonaux à une même droite sont parallèles entre eux.

5) Si deux plans sont parallèles, alors toute droite orthogonale à l’un des deux plans est orthogonale à l’autre plan.

6) Trois perpendiculaires

La droite (AB) est perpendiculaire au plan α en A. La droite (d) est dans P. (AC) est perpendiculaire à (d) dans le plan P. Quel que soit B, point de (AB), on démontre facilement que (BC) est perpendiculaire à (d) : il suffit de remarquer que la droite (d) est perpendiculaire au plan (ABC).

Méthode 1 Démontrer qu’une droite est orthogonale à un plan en un point, on peut chercher :

• deux droites sécantes en ce plan et orthogonales à la droite donnée ;

• une droite parallèle à cette droite et orthogonale au plan ;

• un plan parallèle au plan et orthogonal à la droite.

Méthode 2 Pour montrer que deux droites en un point sont perpendiculaires, on peut chercher un plan orthogonal en ce point à l’une d’elles et contenant l’autre.

Définitions

4) La projection orthogonale sur un plan

Par un point A quelconque il passe une et une seule perpendiculaire au plan P : elle coupe P en A`, appelé projeté orthogonal de A sur le plan P. Si A est dans P, il est confondu avec son projeté sur P. La longueur AA` est la distance du point A au plan P.

5) La distance de deux points est la longueur du segment qui les joint.

6) La distance du point A la droite (d) est égale à AH où H désigne le pied de la perpendiculaire à (d) passant par A.

7) L’angle d’une droite et d’un plan est l’angle formé par la droite et sa projection orthogonale sur le plan.

Exercices

258) Dire, pour chacune des quatre affirmations portant sur le cube ABCDEFGH

représenté ci-contre, si elle est vrai ou fausse.

a) La droite (ED) est orthogonale au plan (AHG).

b) La droite (EF) est orthogonale au plan (ABF).

c) La droite (AD) est orthogonale au plan (HCF).

d) La droite (EH) est orthogonale au plan (BCG).

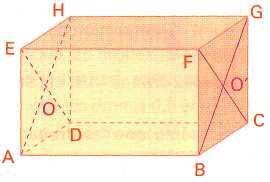259) ABCDEFGH est un parallélépipède rectangle dont les faces ADHE et BCGF sont des carrés de centres respectifs O et Déterminer, en justifiant les réponses :

a) une droite perpendiculaire aux droites (EF) et (BC).

b) une droite perpendiculaire aux droites (HG) et (FC).

c) une droite perpendiculaire aux droites (BD) et (EF).

d) une droite perpendiculaire aux droites (BG) et (ED).

260)

Soit un carré ABCD de côté a. Soit (EA) la perpendiculaire au plan (ABC). Démontrer que les droites (DB) et (EC) sont orthogonales.

261) SABCD est la pyramide de hauteur [SA] à base carrée représentée ci-dessous.

Nommer :

a)une droite perpendiculaire à la droite (BC).

b) une droite orthogonale et non coplanaire à la droite (BC).

c) une droite orthogonale et non coplanaire à la droite (DB).

d) une droite orthogonale et non coplanaire à la droite (SB).

Dans chacun des cas suivants, nommer une droite orthogonale au plan donné :

a) plan (SAB) ; b) plan (ADC) ; c) plan (SAD) ; d) plan (SAC).

262) Soit ABCDEF un prisme droit de bases ABC et DEF, le triangle ABC étant rectangle isocèle en B.

Compléter les phrases par « parallèles » ou « orthogonaux » :

a) La droite (DE) et le plan (ABC) sont … .

b) La droite (EB) et le plan (ABC) sont … .

c) La droite (EF) et le plan (ABD) sont … .

263) On considère un triangle ABC rectangle en

B et sur la droite passant par B orthogonale au

plan (ABC) un point M. Démontrer que la droite

(BC) est orthogonale au plan (ABM).

2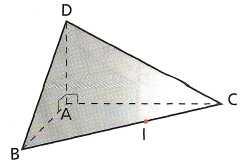64) Soit un tétraèdre DABC ; les faces ABD et ACD

sont des triangles rectangles. Soit I est un point

sur le segment [AB]. Démontrer que le triangle

ADI est rectangle.

265) La droite (KC) est orthogonale au plan (ABC).

ABCD est un carré qui est dans ce plan.

Trouver KB si KA = cm et AC = cm.

266) ABC est un triangle rectangle en C. La droite (MA) est orthogonale au plan (ABC). Démontrer que

267)

La droite (KA) est orthogonale au plan (ABC). ABCD est un losange qui est dans ce plan. Trouver KC si KB = cm, BC = cm et

268) Soit ABC est un triangle. La droite (MA) est orthogonale au plan (ABC). D est un point du côté [BC] tel que Démontrer que [AD] est une hauteur du triangle ABC.

269)

Soit ABCD un rectangle. (MB) est perpendiculaire aux côtés [AB] et [BC] de ce rectangle. Démontrer que la droite (CD) est orthogonale au plan (MBC).

270) Soit ABCD un carré. (SB) est orthogonale au plan (ABC). Préciser la nature du triangle SAD.

271) Soit ABC un triangle rectangle en C. La droite (BM) est orthogonale au plan (ABC). Quelle est la nature du triangle MAC ?

272) La distance du point M aux sommets du carré ABCD est égale à 5cm. Trouver la distance du point M au plan (ABC), si la diagonale du carré est égale à 6cm.

273) La distance du point M aux côtés du carré ABCD est égale à 13cm. Trouver la distance du point M au plan (ABC), si le côté du carré est égal à 10cm.

274) Le point O est le centre du carré ABCD de 4cm de côté. La droite (SO) est orthogonale au plan (ABC). Calculer la distance du point S aux sommets du carré, si AO = cm.

275) Soit le carré ABCD de 5cm de côté. (DM) est orthogonale au plan (ABC), DM = 12 cm. Calculer MA et MC.

276) Soit ABCD un carré dont les diagonales sont sécantes en O. La droite (AM) est orthogonale au plan (ABC). Démontrer que la droite (BD) est orthogonale au plan (AMO).

277) Soit ABCD un rectangle. La droite (DK) est orthogonale au plan (ABC). La distance du point K au côté [AB] est égale à 2,4cm. La distance du point K au côté [BC] est égale à 2,8cm. Trouver DK.

278) ABC est un triangle isocèle de côté cm. La droite (AK) est orthogonale au plan (ABC) et AK = 4cm. Trouver la distance du point K au côté [BC].