Exercices
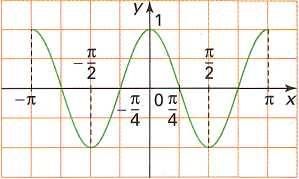196)
On
donne ci-dessous la courbe représentative dans un repère orthogonal
de la fonction f définie par
a) Quelle propriété de la courbe représentative permet de conjecturer que la fonction f est paire ?
b) Démontrer que la fonction f est paire.
c) Trouver la période de cette fonction.
d) Dresser
le tableau de variation de cette fonction pour
.
197)
Démontrer
que la fonction f définie sur R par
est
périodique de période 6π.
198)
Soit
f la fonction définie sur R
par
Vérifier que pour tout réel x,
Que
peut-on dire de la fonction f ?
199)
Soit f la fonction définie sur R
par
a) Démontrer que la fonction f est impaire.
b) Démontrer que la fonction f est périodique de période π.
c) Donner
la représentions graphique de f sur l’intervalle
d) Décrire
les variations de la fonction f sur l’intervalle
200) Trouver la période des fonctions suivantes :
a)
b)
c)
d)
201) Donner la représentions graphique en explicitant clairement l’amplitude et la période des fonctions suivantes :
a)
b)
c)
d)
e)
f)
g)
h)
202) Donner la représentions graphique en explicitant clairement l’amplitude et la période des fonctions suivantes :
a)
b)
c)
d)
203) Donner la représentions graphique en explicitant clairement l’amplitude et la période des fonctions suivantes :
a)
b)
c)
d)
204) Donner la représentions graphique en explicitant clairement l’amplitude et la période des fonctions suivantes :
a)
b)
c)
d)
205) Donner la représentions graphique des fonctions suivantes :
a)
b)
c)
206) Déterminer la période et l’ensemble des images des fonctions suivantes :
a)
b)
c)
d)
3.4 Équations trigonométriques
Mots à retenir
les formules de duplication (формулы двойного угла)
les formules de linéarisation (формулы понижения степени)
le changement de variable (замена переменной)
Pour résoudre certaines équations et inéquations où figurent des fonctions trigonométriques, il est parfois nécessaire de procéder à des transformations d’écritures qui se reposent sur les identités suivantes.
Formules d’addition
Formules de duplication
Formules de linéarisation
Transformer le produit en somme
Transformer la somme en produit
Au moyen
des fonctions trigonométriques, on rencontre des équations
d’inconnue x du type
etc.
Les équations trigonométriques avec sinus
L’équation
élémentaire
n’a
pas de solutions si
a
une infinité de solutions si
L’équation
élémentaire
,
où
est une constate, admet pour solution :
ou
Par
conséquent, la solution peut être écrite :
avec
k entier relatif.
Exemple :
résoudre
équivaut
à
d’où
ou
On
peut écrire aussi
Les équations trigonométriques avec cosinus
L’équation
élémentaire
n’a
pas de solutions si
a
une infinité de solutions si
L’équation
élémentaire
,
où
est une constate, admet pour solution :
ou
Par
conséquent, la solution peut être écrite :
avec
k entier relatif.
Exemple :
résoudre
équivaut
à
,
soit
ou
Ce
qui correspond à
Les équations trigonométriques avec tangente
L’équation
élémentaire
où
est une constate, admet pour solution
avec k entier relatif.
Remarque
Avant d'aborder directement la résolution d'une équation trigonométrique élémentaire, il peut s'avérer utile de simplifier son expression. Beaucoup d’équations se ramènent aux équations élémentaires ou à une équation du deuxième degré, en utilisant les formules trigonométriques.
Méthode1 Équation du deuxième degré
Si l’équation est du deuxième degré en sin x, cos x ou tan x, on pose sin x = y,
cos x = y ou tan x = y. On résout ensuite l’équation du deuxième degré en y et on est ainsi ramené à des équations élémentaires.
Exemple :
résoudre l’équation
Soit
Le
changement de variable conduit à l’équation du second degré en
y:
dont
les solutions sont
et
Il
reste à résoudre
et
La
première équation n’a pas de solutions. Les solutions de seconde
sont
avec k entier relatif. Ce sont les solutions de l’équation
initiale.
Méthode2
L’équation du type
Soit a, b
et c constantes non nulles. Transformation du premier membre. Mettons
en facteur le réel
où
Il existe
un réel α de
tel
que
et
Donc
d’où
Il reste
résoudre l’équation
L’équation
initiale peut se résoudre en utilisant les formules :
où
On
obtient une équation d’inconnue t :
