3. Fonctions trigonométriques

3. 1 Trigonométrie dans un triangle rectangle

Mots à retenir

un rapport, une relation (отношение) une grandeur (величина)

le côté adjacent à l’angle (сторона, прилежащая к углу)

le côté adjacent opposé à l’angle (сторона, противолежащая углу)

Définitions

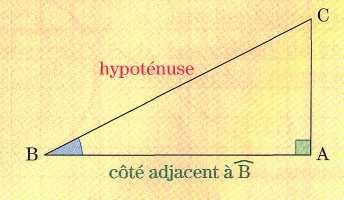Dans un triangle rectangle

• Le cosinus d’un angle aigu est le quotient de la longueur du côté de l’angle droit adjacent à cet angle par la longueur de l’hypoténuse.

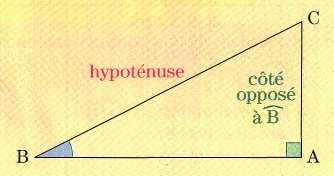
• Le sinus d’un angle aigu est le quotient de la longueur du côté de l’angle droit opposé à cet angle par la longueur de l’hypoténuse.

• La tangente d’un angle aigu est le quotient de la longueur du côté de l’angle droit opposé à cet angle par la longueur du côté de l’angle droit adjacent à cet angle.

Relations entre cosinus, sinus, tangente

Pour tout angle aigu x : et

Remarques

• Le cosinus, le sinus et la tangente d’un angle aigu ne dépendent que de la mesure de cet angle.

• Le cosinus et le sinus d’un angle aigu sont toujours compris entre 0 et 1 car, dans un triangle rectangle, l’hypoténuse est toujours le plus grand côté.

• On peut écrire les relations de la façon suivante :

Le cosinus, le sinus et la tangente sont des outils qui permettent de calculer des longueurs de segments et des mesures d’angles dans des triangles rectangles.

Méthode : utiliser la trigonométrie

• Avoir un triangle rectangle dont un côté est le segment cherché,

• Connaître l’un des angles aigus du triangle rectangle et la mesure d’un côté.

Tableau de valeurs particulières

x	30°	45°	60°
sin x
cos x
tan x		1

Exercices

147) Écrire, et de deux façon

différentes avec les lettres de la figure ci-contre.

148) Soit le triangle MNP rectangle en M. Compléter les phrases ci-dessous par « le cosinus », « le sinus » ou « la tangente ».

a) Si on cherche l’angle et que l’on connaît MP et MN, on utilise … .

b) Si on cherche l’angle et que l’on connaît NP et MN, on utilise … .

c) Si on cherche l’angle et que l’on connaît MP et NP, on utilise … .

d) Si on cherche MN et que l’on connaît MP et l’angle, on utilise … .

e) Si on cherche MN et que l’on connaît PN et l’angle, on utilise … .

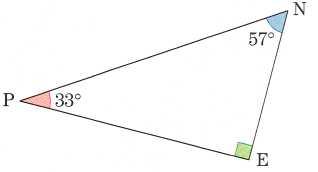149) Dans chacun des cas suivants, écrire avec sinus ou cosinus, une relation qui lie les grandeurs données.

a) NE, PN, 33°

b) NE, PN, 57°

c) PE, PN, 33°

d) PE, PN, 57°

150) En utilisant les informations portées sur les deux figures ci-dessous, calculer pour chacune d’elles l’arrondi de FG à 0,1cm près.

151) On donne le triangle rectangle en A. Exprimer chaque nombre de la première colonne sous la forme d’une fraction dans deuxième colonne.

152) Les triangles ABC et ACD sont rectangles respectivement en B et en D.

a) Pour chacun des angles suivants, préciser son côté adjacent, son côté opposé et le triangle considéré :

b) Écrire sous forme fractionnaire le sinus de chacun des angles.

c)Même question pour le cosinus puis la tangente de chacun de ces angles.

153) On donne le triangle ERT rectangle en E. On sait que = 2 et

TE = 2,5cm. Combien mesure RE ?

154) Le triangle ARN est rectangle en N. et RN = 1,8cm. Calculer la valeur exacte de AN puis donner son arrondi au mm.

155) Le triangle ABC est rectangle en B. et AB = 2 ,4cm. Calculer la valeur exacte de AN puis donner son arrondi au mm.

156) Le triangle TSR est rectangle en S. SR = 4cm, TR = 6cm. Calculer arrondi au degré de l’angle

157) Le triangle ABC est rectangle en B. et BC = 8cm. Calculer la valeur exacte de AC et de AB. Puis donner l’arrondi au mm de AC et de AB.

158) Le triangle TSR est rectangle en S. SR = 8cm, ST = 4,6cm. Calculer arrondi au degré de l’angle

159) Le triangle PEI est rectangle en E. et PI = 6,6cm. Calculer la valeur exacte de EI et de PE puis donner l’arrondi au mm de EI et de PE.

160) Arthur veut connaître la hauteur d’un arbre. Il dispose d’un appareil de mesure dont l’objectif est situé au point A, à 1,70 m au-dessus du sol. Ce point A est à 60 mètres de l’arbre. Le sol est horizontal. Il mesure l’angle. Il trouve 23°. Calculer la hauteur de cet arbre.

161) Un cartographe doit déterminer la largeur DC d’une rivière. Voici les relevés qu’il a effectués sur le terrain : AB = 100 m, = 60°, = 22°,

= 90°. Calculer la largeur DC de la rivière à 1 mètre près.

1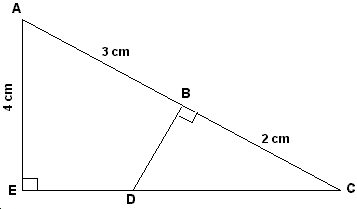 62) En utilisant les données de la figure, calculer la longueur BD.

163) Soit x est un angle aigu tel que Calculer sin x et tan x. On donnera les résultats sous la forme

164) ABC est un triangle rectangle en B. H est le pied de la hauteur issue de B.

On donne : AB= 8 cm, BH= 4 cm,

a) Calculer, en centimètres, la mesure du segment [AH], arrondie au mm.

b) Calculer, en centimètres, la mesure du segment [HC], approchée à 0,1 prés par défaut.

c) Soit J le point du segment [AC] tel que

= . La parallèle à la droite (BC) passant par J coupe le segment [AB] en K. Expliquer pourquoi AK=2 cm.

165) Un câble de 20 m de long est tendu entre le sommet d'un poteau vertical et le sol horizontal. Il forme un angle de 40° avec le sol (voir schéma). Calculer la hauteur du poteau.

1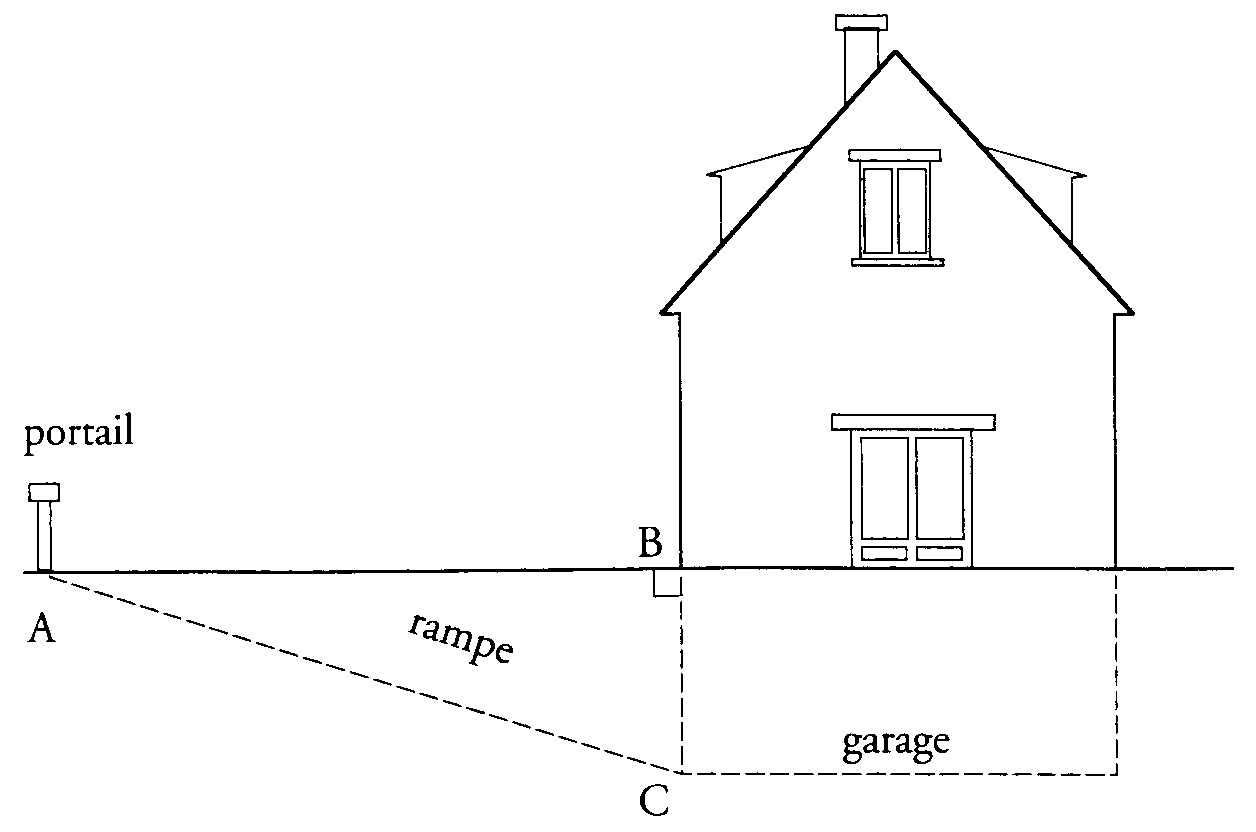66) On accède au garage situé au sous-sol d'une maison par une rampe [AC].

On sait que : AC = l0,25 m ; BC = 2,25 m.

a) Calculer la distance AB entre le portail et l'entrée.

b) Calculer à un degré près par excès la mesure de l’angle.

167) PAR est un triangle rectangle en A et tel que : AP = 3,6 cm ; AR = 4,8 cm ; H est le projeté orthogonal de A sur la droite (RP).

a) Faire la figure.

b) Calculer la longueur du côté [PR].

c) Calculer l'aire du triangle PAR. En déduire AH.

d) Calculer sin. En déduire l'arrondi au degré près de la valeur de l’angle.

168) La figure ci-dessous est volontairement inexacte.

a) L’unité étant le cm, faire une figure aux mesures exactes.

b) Démontrer que le triangle ACD est rectangle en C.

c) Quelle est la nature du triangle ABD ? Justifier.

Calculer l'aire du triangle ABD en cm².

d) Calculer la mesure de l'angle au degré près. En déduire, sans nouveau calcul, une valeur approchée de la mesure de l’angle.

169) Soit x est un angle aigu. Calculer sin x et tan x, si cos x = .

170) Soit x est un angle aigu. Calculer cos x et tan x, si sin x = .

171) Soit x est un angle aigu. Existe-t-il un angle x tel que : sin x = et

cos x = .

172) La pente d’une route, d’un toit est la tangente de l’angle que forme cette route, ce toit avec l’horizontale.

La pente s’exprime souvent en pourcentage : une pente de 25% correspond à un angle avec l’horizontale tel que tan α = 0,25. Un train à crémaillère se déplaçant à la vitesse de 1,2 km.h ^-1 met 25 minutes pour aller de A à B sur une pente de 25%.

Calculer la différence d’altitude BH entre A et B.

173) Démontrer que pour tout angle aigu x :

174) Soit x est la mesure d’un angle aigu d’un triangle rectangle. Démontrer que