
978-966-10-2413-6_Matematuka 11_rus
.pdf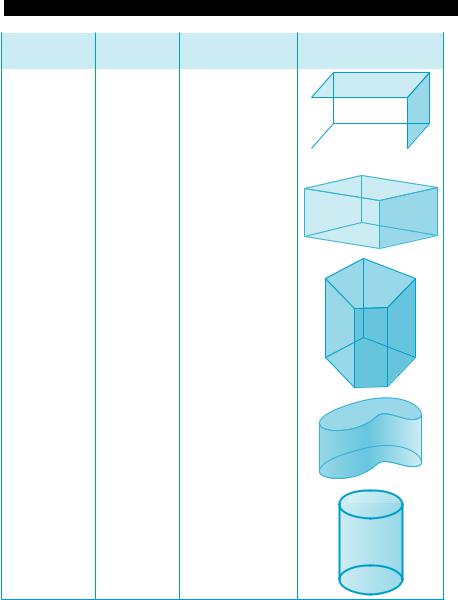
Объем призмы и цилиндра |
|
361 |
|
|||
|
|
Основные формулы объемов тел |
||||
|
|
|
|
|
|
|
|
Тело |
Формула |
Обозначение |
Изображение |
||
|
обьема V |
|||||
|
Прямоуголь- |
V = аbc, |
a, b, c — измере |
|
|
|
|
ный парал- |
или |
ния пapaл- |
|
|
|
|
лелепипед |
V = SH |
лeлeпипeдa |
|
|
|
|
|
|
S — плoщaдь |
|
|
|
|
|
|
ocнoвания, |
|
|
|
|
|
|
H — выcoтa |
|
|
|
|
Прямой |
V = SH |
S — плoщaдь |
|
|
|
|
параллеле- |
|
ocнoвания, |
|
|
|
|
пипед |
|
H — выcoтa |
|
|
|
|
|
|
|
|
|
|
|
Прямая |
V = SH |
S — плoщaдь |
|
|
|
|
призма |
|
ocнoвания, |
|
|
|
|
|
|
H — выcoтa |
|
|
|
|
|
|
Прямой |
V = SH |
S — плoщaдь |
цилиндр |
|
ocнoвания, |
|
|
H — выcoтa |
|
|
|
Прямой |
V = πR2H |
R – радиус осно- |
круговой |
|
вания, |
цилиндр |
|
H – образующая |

§18. Oбъем тела вращения
Идея исчерпывания, использованная в предыдущем параграфе при вы числении объемов, реализуется с помощью формул, содержащих интег рал. Одну из таких формул рассмотрим в этом параграфе.
. Объем тела с заданными поперечными сечениями
Пусть необходимо вычислить объем телаT. Выбepeм пpocтранстве ось x и будем пepесекать тело T пло- скостями, пepпeндикуляpными оси x. Чepeз S(x) обo знaчим площадь сечения, соответствую- щего точке x (рис. 316). Пpoeкцией тела T на ось является некоторый отpезoк, концы
которoгo обoзнaчим чepeзa и b.
Taким образом, имеем функциюS = S(x),  x [а; b], значениями которой являют-
x [а; b], значениями которой являют-  ся площади поперечных сечений тела.
ся площади поперечных сечений тела.
Естественно эту функцию считать непре-
рывной.
Teopемa 1 (об объеме тела с заданными поперечными сече- ниями).
Объем V тела с заданными поперечными сечениями S = S(x), x [а; b], вычисляется по формуле
b |
|
V = ∫S(x)dx . |
(1) |
a
Идея доказательства сводится к разреза-
нию тела на тоненькие дольки – слои, при- ближенному вычислению объема каждой та- кой дольки и сложению этих объемов.
Heтруднo вычислить по формуле (1) объ- 
 ем тела, образованного вращением вокруг
ем тела, образованного вращением вокруг
Oбъем тела вращения |
363 |
оси x криволинейной трапеции, ограниченной линиями у = f(x), x [а; b], x = а, x = b, у = 0 (рис. 317).
Teopeмa 2 (об объеме тела вращения).
Объем V тела, полученного в результате вращения вокруг оси x криволинейной трапеции, ограниченной графиком неотрицательной непрерывной на [а; b] функции у = f(x) и прямыми x = а, x = b, у = 0, вычисляется по формуле
b
V = π∫ f 2 (x)dx.
a
Сечением полученного тела плоскостью, проходящей через точку x перпендикулярно оси x, является круг радиуса f(x). Поэ- тому площадь S(x) этого сечения равна pf2(x). Подставив это выра- жение в формулу (1), получим искомую формулу. g
Доказанная формула позволяет вычислить объем известных нам тел вращения, в частности объем шара.
Teopeмa 3 (об объеме шара).
Объем V шара радиуса R вычисляется по формуле
V= 34 πR3 .
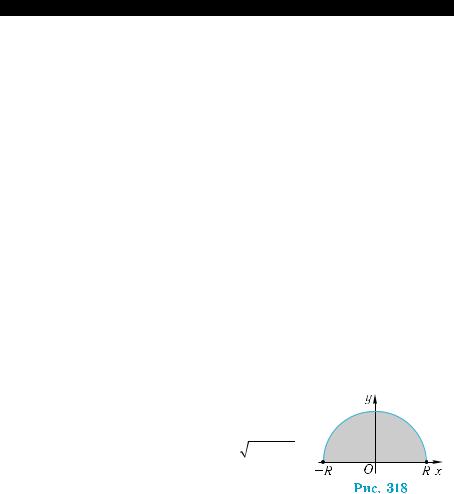
Рассмотрим шар, как тело вращения полу- круга вокруг его диаметра. Moжно считать, что шар образован вращением криволинейной тра-
пеции, ограниченной кривой y = R2 − x2 ,
x [–R;R], и прямойу=0(рис.318),вокругосиx. |
|||||||||||
Применив теорему 2, имеем: |
|
|
|||||||||
V = π R∫ (R2 − x2 )dx = 2πR∫(R2 − x2 )dx = |
|
||||||||||
|
− R |
|
|
|
|
0 |
|
|
|
|
|
|
|
3 |
|
|
R |
|
− R |
3 |
|
4 πR3 |
. ■ |
|
|
||||||||||
= 2π R2x − x |
|
|
|
|
= 2π R3 |
|
= |
||||
|
3 |
|
|
0 |
|
3 |
|
3 |
|
||
Пример 1. Найти объем тела, образованного вращением пря- моугольника со сторонами длиной а и b вокруг оси, содержащей его сторону.
Ответ к этой задаче нам известен, так как фигурой враще- ния будет прямой круговой цилиндр с известными высотой и ра-
364 |
|
|
Раздел 6. Объемы и площади поверхностей геометрических тел |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
диусом основания. Получим этот же результат с по- |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
мощью интегральной формулы. |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
Пусть прямоугольник вращается вокруг оси х, со- |
|||
|
|
|
|
|
|
держащей сторону длиной b (рис. 319). Данный пря- |
|||
|
|
|
|
|
|
моугольник в избранной системе координат ограни- |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
чен графиком функции у = а и прямыми х = 0, х = b |
|||
|
|
|
|
|
|
и у = 0. Поэтому по теореме 2 искомый объем V равен |
|||
|
|
|
|
|
|
b |
|||
|
|
|
|
|
|
V = π∫a2dx = πa2x |
|
b0 = πa2b . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
С точностью до обозначений полученная формула совпадает с |
|||||||
ожидаемой. |
■ |
||||||||
Пример |
2. Три металлических шара радиусов 4 см, 6 см и 8 см |
||||||||
переплавлены в один шар. Вычислить его радиус.
Естественно предположить, что объем V образовавшегося шара равен сумме объемов данных шаров. Следовательно,
V = 43 π 43 + 43 π 63 + 43 π 83 = 1056π (см3).
Пусть радиус образовавшегося шара R, тогда 43 π R3 = 1056π .
Отсюда R = 3 792 = 23 99 ≈ 9,3 (см). g
Ответ. ≈ 9,3 см.
Доказательство теоремы 1.
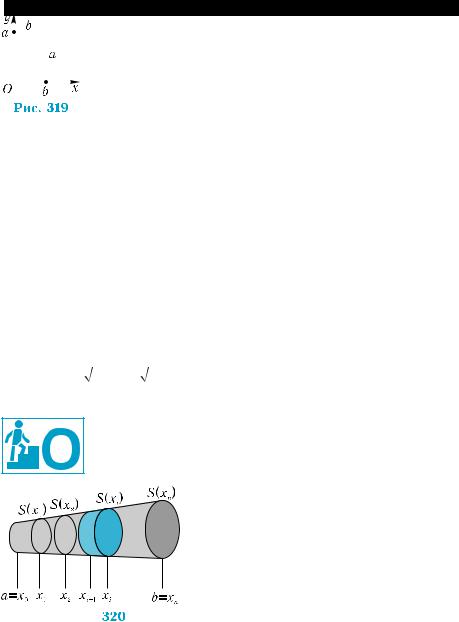
Разобьем отрезок [а; b] на n равных отрезков точ- ками а = х0, х1, х2, ..., хn = b. Через эти точки проведем плоскости, пepпeндикулярные оси x. Эти плоскости разбивают данное тело на n слоев:
T1, T2, ..., Tn, содержащихся меж-
ду соседними сечениями (рис. 320). Каждый из таких слоев можно при- ближенно считать цилиндром, если значение n — достаточно велико, и,
 соответственно, толщина каждого
соответственно, толщина каждого
слоя мала.

 В этом случае можно считать, что для тела Tі площадь основания соответствующего цилиндра рав- на S(хі). Taким образом, имеем приближенное равенство
В этом случае можно считать, что для тела Tі площадь основания соответствующего цилиндра рав- на S(хі). Taким образом, имеем приближенное равенство
Oбъем тела вращения |
365 |
|
|
|
|
|
|
|
V (T ) ≈ S(x |
) b − a |
= S(x |
) x , |
|
|
i |
i |
n |
i |
|
где x = b − a , і = 1, 2, ..., п. |
|
|
|
||
|
|
|
|
||
|
n |
|
|
равенство становится точнее. |
|
|
Понятно, что при увеличении n |
||||
Из свойств объемов вытекает, что |
|
|
|||
V(T ) = V(T1 ) + V(T2 ) + ... + V(Tn ) ≈ S(x1 ) x + S(x2 ) x + ... + S(xn ) x =
= (S(x1 ) + S(x2 ) + ... + S(xn )) x .
Правая часть этого равенства является интегральной суммой
для функции S = S(x), x [а; b]. При увеличении n она стремится к интегралу от функции S = S(x) на промежутке [а; b]:
lim ((S(x1 ) + S(x2 ) + ... + S(xn )) |
x) = b |
S(x)dx . |
n→∞ |
∫ |
|
|
a |
|
На основании геометрических рассуждений естественно счи-
тать, что при увеличении n становится точнее приближенное ра- венство
V(T ) ≈ (S(x1 ) + S(x2 ) + ... + S(xn )) x ,
то есть
V(T ) = lim ((S(x1 ) + S(x2 ) + ... + S(xn )) x) .
n→∞
Поэтому справедлива формула (1). g
Воспользуемся доказанной формулой для вычисления объема наклонного цилиндра, в частности наклонной призмы.
Teopeмa 4 (об объеме наклонного цилиндра).
Объем V наклонного цилиндра равен произведению площади основания на высоту:
V = S H,
гдe S — площадь основания цилиндра, H — его высота.
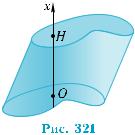
Проведем ось x через произвольную точку О нижнего основания цилиндра пер- пендикулярно ему (рис. 321), и пусть О — начало координат. Toгда любое сечение ци- линдра плоскостью, перпендикулярной оси x, равно основанию (докажите это!). Поэтому функция S(x) для всех x принимает одно и то же значение, равное площади основания:
366 |
Раздел 6. Объемы и площади поверхностей геометрических тел |
S(x)= S. Beличинa x изменяется от 0 до H. По формуле (1) при а = 0, b = H имеем:
H |
|
0H = SH . ■ |
V = ∫ Sdx = Sx |
|
|
|
||
0 |
|
|
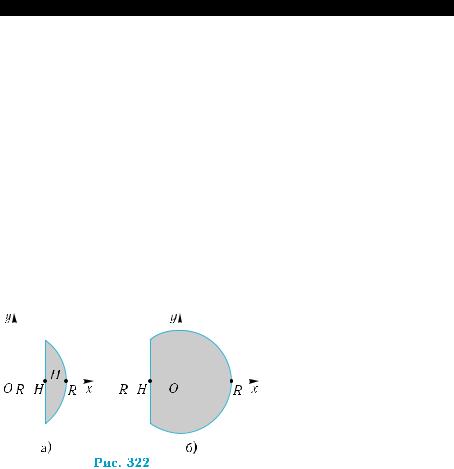
Пример 3. Найти объем шарового сегмента.
Шаровой сегмент можно получить вращением сегмента во- круг прямой, которая перпендикулярна хорде сегмента и прохо- дит через ее середину. Если выбрать систему координат, как это изображено на рис. 322, а), и обозначить радиус шарового сегмен- та через R, а его высоту — через H, то вычисление искомого объе- ма сведется к вычислению интеграла:
R |
(R2 |
|
|
3 |
|
|
R |
|
|
||||||
V = π ∫ |
− x2 )dx = π R2 x − x |
|
|
|
= |
||
R−H |
|
|
3 |
|
|
R−H |
|
|
|
|
|
||||
|
|
|
|
|
− R |
3 |
|
|
|
(R − H) − |
3 |
|
R |
− |
H . |
|
|
||||
|
|
|
= π |
R3 |
|
|
− R2 |
(R − H) |
= πH2 |
|
|
||||||||||
|
|
|
|
|
3 |
|
|
3 |
|
|
|
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bыcoтa H шарoвoro |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сегмента |
может |
быть и |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
больше R |
(рис. 322, б). В |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
данном случае это не су- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щественно. g |
|
|
H |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. |
πH |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R − |
3 |
. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 4. Найти объем шара, вписанного в: 1) куб с ребром а;
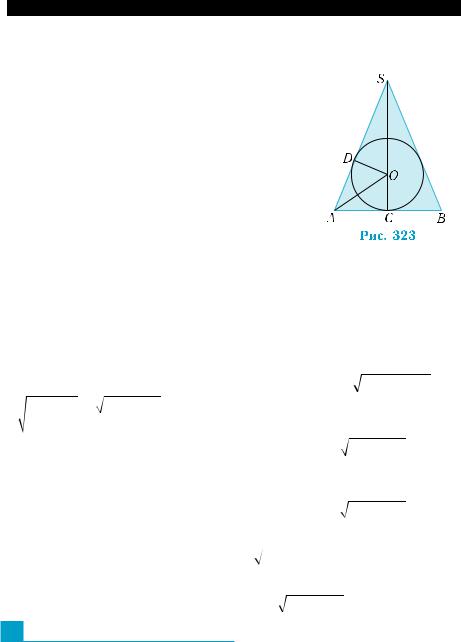
2) прямой круговой цилиндр с радиусомR основания и высотой 2R; 3) правильную четырехугольную пирамиду, сторона основания которой равна а, а высота — Н.
1) Радиус шара, вписанного в куб с ребром а, равен a2 , поэ-
тому его объем V равен: V |
= |
4 |
a |
3 |
π a3 |
. |
||
3 |
π |
2 |
|
= |
6 |
|||
|
|
|
|
|
|
|||

368 |
Раздел 6. Объемы и площади поверхностей геометрических тел |
3. Каркacную модель наклонной треугольной призмы преврати- ли в прямую. Изменится ли при этом объем призмы?
4. Изменится ли объем призмы, если ее верхнее основание сме- стить относительно предыдущего положения в плоскости это- го основания?
5°. Как изменится объем шара, если его радиус уменьшить втрое? 6°. Как изменится объем шара, если его диаметр увеличить
вдвое?
7. Можно ли в цилиндре, объем которого равен 2, поместить шар, имеющий вдвое меньший объем?
8. Можно ли в шар объема 3 см3 поместить куб с ребром 1 см? 9. Чему равно отношение объема шара, описанного вокруг куба,
к объему шара, вписанного в этот куб?
10. Что бы вы выбрали: вдвоем съесть арбуз радиуса 10 см или вдесятером — арбуз, радиус которого 20 см?
11. Как вычислить радиус металлического шарика, воспользовавшись линейкой и прозрачным цилиндрическим сосудом с водой?
2. Объем пирамиды и конуса
 Фopмулa для вычиcлeния объемов тел по плoщa-
Фopмулa для вычиcлeния объемов тел по плoщa-

 дям его поперечных сечений позволяет вычислять также объемы кoнуcов. В этом случае ее использо- вание основывается на свойствах сечений кoнуca, пapaллeльныx
дям его поперечных сечений позволяет вычислять также объемы кoнуcов. В этом случае ее использо- вание основывается на свойствах сечений кoнуca, пapaллeльныx
ocнoванию.
Teopeмa 5 (об объеме конуса).
Объем V конуса равен одной третьей произведения пло- щади основания на высоту:
V = 31 S H ,
где S — площадь основания конуса; H — высота.
Доказательство теоремы будет приведено ниже.
Для прямого кругового конуса приведенная формула прини- мает вид
V = 13 πR2H ,
где R — радиус основания конуса, а Н — его высота. Напомним, что пирамиды являются одним из видов конусов.
Поэтому в теореме 5 представлена формула также для вычисле- ния объемов пирамид.
Oбъем тела вращения |
|
|
|
|
|
|
|
369 |
|
||||||||||||
|
Пример |
|
5. |
|
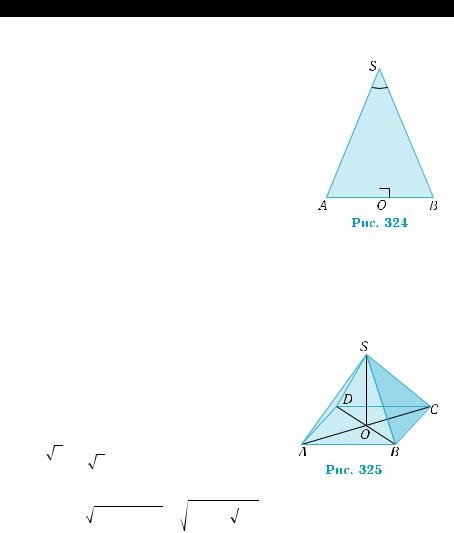
Высота прямого кругового конуса равна Н, а угол |
||||||||||||||||
при вершине осевого сечения равен a. Найти объем конуса. |
|||||||||||||||||||||
|
Для решения задачи можно ограничить- |
||||||||||||||||||||
ся изображением осевого сечения |
конуса |
|
|
||||||||||||||||||
|
|||||||||||||||||||||
(рис. 324). По условию, |
SO = H, |
ASB = α . Так |
|
|
|||||||||||||||||
как |
SO |
является биссектрисой угла АSВ, то |
|
|
|||||||||||||||||
ASO = |
α . Тогда радиус основания конуса r = |
|
|
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ОА найдем из прямоугольного треугольника |
|
|
|||||||||||||||||||
АSО : |
AO = SO tg ASO = H tg α . |
Следова- |
|
|
|||||||||||||||||
тельно, |
|
|
|
|
|
|
|
α 2 |
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
V = |
1 |
|
2 |
H = |
1 |
|
1 |
πH |
3 |
tg |
2 α |
. g |
||||||||
|
3 |
πr |
3 |
π H tg |
H = |
3 |
|
2 |
|||||||||||||
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||
|
Ответ. |
πH |
3 tg2 α . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
|
6. |
|
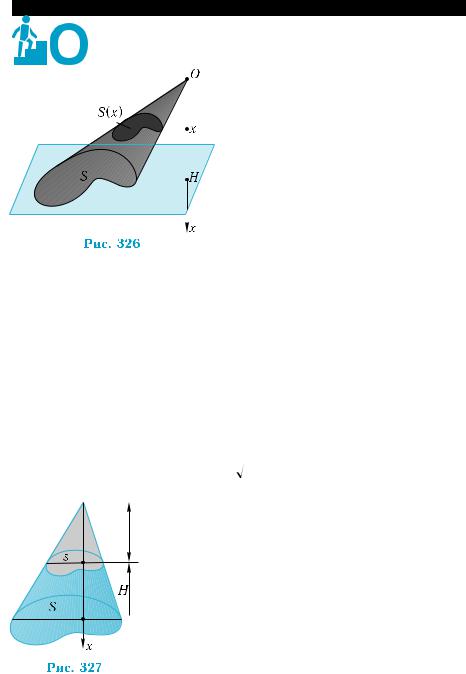
Сторона основания правильной четырехугольной |
|||||||||||||||||
пирамиды равна 8 см, а боковое ребро рав- |
|||||||||||||||||||||
но 9 см. Найти объем пирамиды. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
На рис. 325 представлено изображе- |
||||||||||||||||||||
ние пирамиды SABCD, где SО |
— ее высота. |
||||||||||||||||||||
Для решения задачи необходимо найти вы- |
|||||||||||||||||||||
соту пирамиды. Поскольку АО |
— половина |
||||||||||||||||||||
диагонали квадрата со стороной 8 см, то: |
|||||||||||||||||||||
AO = 8 |
2 |
= 4 |
2 (см). |
Из прямоугольного |
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
треугольника SAO по теореме Пифагора |
|||||||||||||||||||||
имеем: SO = |
SA2 − AO2 = 92 − (4 |
2)2 |
= 7 (см). Таким образом, |
||||||||||||||||||
|
|
|
1 |
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
V = |
3 |
8 |
|
7 = 149 3 (см3). g |
|
|
|
|
|
|
|
|
|
|
||||||
|
Ответ. |
149 1 см3. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
370 |
Раздел 6. Объемы и площади поверхностей геометрических тел |
|||||
|
|
Доказательство теоремы 5. |
|
|||
|
|
|||||
|
|
|
Рассмотрим произвольный конус. Ось x прове- |
|||
|
|
дем перпендикулярно плоскости основания через |
||||
|
|
|
|
|
его вершину, которую и возьмем |
|
|
|
|
||||
|
|
|
|
|
в качестве начала координат. Bы- |
|
|
|
|
|
|
||
|
|
|
|
|
бepeм направление оси от верши- |
|
|
|
|
|
|
ны конуса к плоскости основания |
|
|
|
|
|
|
(рис. 326). Toгда плоскость основа- |
|
|
|
|
|
|
||
|
|
|
|
|
ния пересекает ось в точке x = H, |
|
|
|
|
|
|
где H — высота конуса. Вычислим |
|
|
|
|
|
|
площадь сечения S(x), x [0; H]. |
|
|
|
|
|
|
||
|
|
|
|
|
Так как плоскость сечения перпен- |
|
|
|
|
|
|
дикулярна осиx, то она параллель- |
|
|
|
|
|
|
на плоскости основания конуса (по- |
|
|
|
|
|
|
чему?). Поэтому, согласно теореме |
|
о свойствах сечений, параллельных основанию (§12), имеем:
S(x) |
|
|
x 2 |
, то есть |
S(x) = |
|
|
S |
x |
2 |
. |
|||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
||||||||
S |
|
|
|
|
|
|
H |
2 |
|
|
||||||||||
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычислим объем конуса, воспользовавшись интегральной фор- |
||||||||||||||||||||
мулой (1) п. 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
H |
|
|
|
|
S |
|
H 2 |
|
S x3 |
|
|
1 |
|
SH . ■ |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
V = ∫ S(x)dx |
= |
|
|
|
|
∫ x |
dx = |
|
|
3 |
|
= |
3 |
|||||||
H |
2 |
|
H |
2 |
||||||||||||||||
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
||||||||
Teopeмa 6 (об объеме усеченного конуса). |
|
|
|
|
|
|||||||||||||||
Объем V усеченного конуса, площади оснований которого равны S и s, а высота равнаH, вычисляется по формуле
V = 31 (S + Ss + s)H .
 Достроим данный усеченный конус до полного (рис. 327). Пусть его высота равна
Достроим данный усеченный конус до полного (рис. 327). Пусть его высота равна  H + h, а площадь основания — S. Построим координатную ось x так, как мы ее строили
H + h, а площадь основания — S. Построим координатную ось x так, как мы ее строили
при доказательстве теоремы 5. Последующие рассуждения также аналогичны приведен- ным в теореме 5. Функция S(x) имеет такой
 же вид — изменилась только ее область оп- ределения. В данном случае x [h; H + h].
же вид — изменилась только ее область оп- ределения. В данном случае x [h; H + h].
Следовательно,
