
978-966-10-2413-6_Matematuka 11_rus
.pdf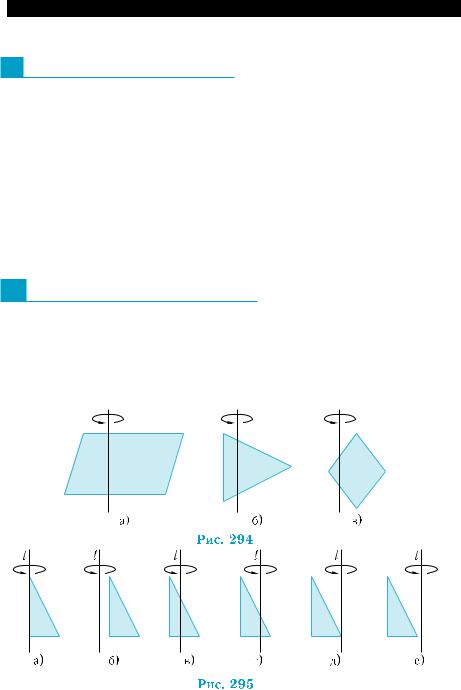
Тела вращения |
331 |
сительно ocи вращения, то общие точки cфep составляют окруж- ность (рис. 293, б). ■
99 Koнтpoльные вопросы
1°. Может ли фигура вращения иметь только одну плоскость симметрии ?
2. Может ли фигура вращения иметь ровно две оси симметрии? 3°. Всякая ли фигура вращения имеет центр симметрии?
4°. Верно ли, что всякое сечение фигуры вращения является кругом? 5°. Можно ли получить пирамиду вращением некоторой фигуры
вокруг оси?
6°. Может ли фигура вращения быть многогранником?
7. Дан прямоугольник со сторонами а и b, а > b. У какого из ци- линдров, полученных в результате вращения прямоугольника вокруг его сторон, площадь развертки всей поверхности больше?
Графические упражнения
1.Изобразите осевое сечение фигуры, образованной вращением вокруг оси фигуры, изображенной на рис. 294, а)–в).
2.Опишите фигуру, образованную вращением прямоугольного треугольника, изображенного на рис. 295, а)–е), вокруг оси, параллельной одному из катетов или совпадающей с прямой, содержащей его.
332 |
Раздел 5. Геометрические тела и поверхности |
Задачи
286.Опишите фигуру, образованную вращением: 1°) треугольника вокруг одной из его сторон;
2)прямоугольника вокруг оси, параллельной одной из его сторон;
3)ромба вокруг оси, содержащей его сторону;
4)круга вокруг оси, не пересекающей его;
5)равностороннего треугольника вокруг оси, параллельной высоте и проходящей внутри треугольника.
287.Вращением какой фигуры и вокруг какой оси можно полу- чить фигуру, форму которой имеет:
1)круглый заостренный карандаш; 2) глиняная миска;
3)зеркальная поверхность прожектора; 4) стакан? Прямоугольник со сторонами 6 см и 8 см вращается вокруг диагонали. Найдите:
1)площадь осевого сечения фигуры вращения;
2)наибольшую и наименьшую площади сечений фигуры вра- щения плоскостями, перпендикулярными оси вращения.
Итог
Основные определения
Пусть даны прямая l и плocкая фигура 
 F, лeжaщие в одной плоскости. Вращая
F, лeжaщие в одной плоскости. Вращая 



 произвольную точку фигуры вокруг пpя- мoй l, получим окружность с цeнтpoм
произвольную точку фигуры вокруг пpя- мoй l, получим окружность с цeнтpoм  на прямой l. Фигуpa, составленная из окружностей вращения вcеx точек фигу-
на прямой l. Фигуpa, составленная из окружностей вращения вcеx точек фигу-
ры F, нaзывaетcя фигуpoй вращения. Пpямaя l нaзывaетcя осью вращения. Tелo, являющееся фигурой вращения,
называется телом вращения, его по-
верхность — поверхностью враще- ния.
Основные утверждения
1.Ось вращения является осью симметрии фигуры вращения, а плоскости, пpoxoдящие через эту ось, являются плоскостя- ми симметрии.
2.Пересечением двух сфер является окружность.

Готовимся к тематиче - скому оцениванию по теме «Геометрические тела и поверхности»
?? Задания для самоконтроля
1°. Всегда ли сечение прямого цилиндра плоскостью, параллель- ной образующей, является прямоугольником?
2°. Всегда ли плоскость, проходящая через середину образующей параллельно основанию, является плоскостью симметрии прямого цилиндра?
3. Можно ли разрезать прямой круговой цилиндр на восемь ча- стей тремя разрезами?
4°. Является ли призма правильной, если все ее боковые гра- ни — равные между собой прямоугольники?
5. Может ли прямая пятиугольная призма иметь только три плоскости симметрии?
6°. Верно ли, что все диагонали параллелепипеда равны между собой и точкой пересечения делятся пополам?
7. Верно ли, что отрезок, соединяющий вершину кругового кону- са с центром его основания, является высотой конуса?
8. Может ли высота конуса иметь с ним лишь одну общую точку? 9°. Верно ли, что все сечения прямого кругового конуса, прохо- дящие через его вершину, являются равнобедренными тре
угольниками?
10. Всегда ли пирамида является правильной, если ее боковые ребра образуют равные углы с высотой?
11°.Равны ли между собой боковые ребра пирамиды, наклонен- ные под одним углом к плоскости ее основания?
12. Могут ли все двугранные углы при основании пирамиды быть равными между собой, если в основании пирамиды лежит прямоугольник с неравными сторонами?
13. Может ли верхнее основание усеченной пирамиды не быть равнобедренным треугольником, если нижним ее основанием является равнобедренный треугольник?

334 |
Раздел 5. Геометрические тела и поверхности |
14.Может ли сечением сферы радиуса R быть окружность радиу-
са 1,1R?
Два сечения сферы имеют одинаковую длину. Верно ли, что секущие плоскости равноудалены от центра сферы?
Может ли прямая иметь с шаром только одну общую точку? Может ли фигура вращения иметь только одну плоскость симметрии?
Ответы к заданиям для самоконтроля
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Да |
да |
да |
нет |
нет |
нет |
нет |
да |
да |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
нет |
да |
нет |
нет |
нет |
да |
да |
нет |
|
Образец контрольной работы №5
1.Высота правильной четырехугольной пирамиды равна 6 см, а боковая грань наклонена к плоскости основания под углом 60°. Найдите:
1°) сторону основания пирамиды; 2) на каком расстоянии от вершины пирамиды следует пере-
сечь ее высоту плоскостью, параллельной основанию, чтобы площадь соответствующего сечения пирамиды была вдвое меньше площади основания; 3*) радиус вписанного шара.
2.Отрезок, концы которого лежат на окружностях обоих осно- ваний прямого кругового цилиндра с высотой Н, пересекает ось цилиндра и наклонен к плоскости основания под углом a. Найдите:
1°) радиус основания цилиндра; 2) площадь сечения цилиндра плоскостью, проходящей через
образующую под углом b к плоскости осевого сечения, прове- денного через ту же образующую; 3*) радиус шара, описанного вокруг цилиндра.
Готовимся к тематическому оцениванию по теме |
335 |
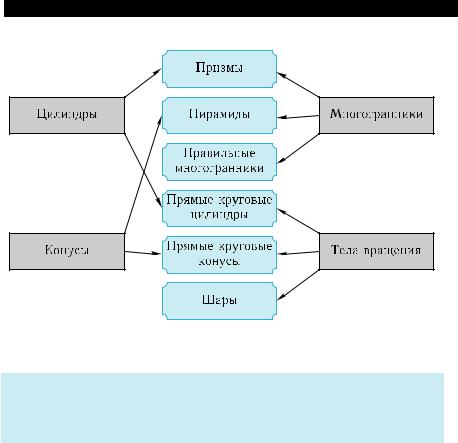
Классификация геометрических тел
Таблица 44
Правильные многогранники
Таблица 45
Тип |
Число |
Число |
|
|
Число |
|
ребер |
Число |
Число |
||||
многогран |
сторон |
вер |
||||
ника |
при вер |
грани |
граней |
ребер |
шин |
|
|
шине |
|
|
|
|
|
Тетраэдр |
3 |
3 |
4 |
6 |
4 |
|
Куб (гексаэдр) |
3 |
4 |
6 |
12 |
8 |
|
Октаэдр |
4 |
3 |
8 |
12 |
6 |
|
Додекаэдр |
3 |
5 |
12 |
30 |
20 |
|
Икосаэдр |
5 |
3 |
20 |
30 |
12 |

Исторический комментарий
Трудно проследить начало истории развития учения о геометри- ческих телах, но, как показывают архитектурные памятники древ- них цивилизаций (Египта, Индии, Китая и т. п.), их строительство невозможно без солидных знаний о соответствующих геометриче- ских образах. Древнегреческие математики выделили основные ге- ометрические тела, открыли много фактов об их строении и свойст- вах. Характерным является и то, что наука о геометрических телах находилась и находится в непрерывном развитии. Так, например, Л. Эйлером в ХVIII ст. была доказана знаменитая теорема о соот- ношении между числами ребер, граней, вершин для (выпуклых) многогранников, а поиск ответа, на какой класс многогранников эта теорема обобщается, привел к развитию учения о свойствах фигур, не изменяющихся при непрерывных деформациях фигур, то есть к становлению новой науки — топологии.
В течение ХІХ ст. вниманием математиков пользовалась про- блема о возможности разбиения равных по объему многогранни- ков на попарно равные части (достаточно назвать знаменитую проблему Д. Гильберта о разбиении двух тетраэдров с равными основаниями и высотами на равные между собой тетраэдры, ре- шенную М. Денном (1878–1952) с отрицательным ответом).
Особое место в истории математики (и вообще, в истории куль- туры, философии) занимают правильные многогранники. Их теория была построена в VI – IV ст. до н.э. Красота и совершен- ство строения этих фигур связывалась с совершенством строе- ния Вселенной. Выдающийся древнегреческий философ Платон (427–347 гг. до н. э.), именем которого порой называют правиль- ные многогранники (Платоновы тела), в своих работах интерпре- тировал элементы (атомы) составляющих природы – земли, воды, воздуха, огня – в виде правильного тетраэдра, куба, октаэдра и икосаэдра. Форму додекаэдра он приписывал всему миру.
Важные открытия в геометрии многогранников принадлежат знаменитому украинскому математику Г.Ф. Вороному (1868–1908). Существенный вклад в теорию поверхностей многогранников внес украинский математик А.В. Погорелов (1919–2002).

ОБЪЕМЫ И ПЛОЩАДИ ПОВЕРХНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ТЕЛ
Измерение геометрических величин (длин, углов, площадей, объемов) является одной из важнейших задач геометрии. В этом разделе рас смотрим задачу измерения объемов геометрических тел и площадей их поверхностей.
Применение геометрии в быту, производстве, технике очень часто свя зано с измерением и вычислением количественных характеристик тел. Важнейшими такими характеристиками тела являются его объем и пло щадь его поверхности.
Измерение величин, в частности геометрических, является сложной ма тематической задачей. Не случайно, что лишь в конце ХІХ – в начале ХХ веков была создана общая теория измерений. Несмотря на то, что клас сические формулы вычисления объемов и площадей поверхностей были известны древнегреческим ученым, для их полноценного обоснования по надобилось практически два тысячелетия. И это вполне понятно. Пока
не удалось формализовать идею предельного перехода, утверждения об измерении величин не имели соответствующего обоснования.
Объемы и площади поверхностей простейших тел вы вычисляли, начиная с начальной школы. Наступило время (как это было и исторически!) осмыс лить эти вычисления, осознать содержание основных понятий, обобщить при емы вычислений величин, овладеть основными методами измерения объемов и площадей поверхностей.
Готовимся к изучению темы «Объемы и площади поверхностей
геометрических тел»
Темой «Объемы и площади поверхностей геометрических тел» завершается рассмотрение геометрических величин, применяе- мых на производстве, в технике, быту и т. п. Оно базируется на опыте измерения длин, углов, площадей плоских фигур. Для под- готовки к изучению темы важнейший учебный материал приве- ден в виде таблиц.
|
Измерение длин, углов, площадей |
||||
|
|
|
Таблица 46 |
||
Название |
Свойства |
Геометрическая |
|||
величины |
иллюстрация |
||||
|
|||||
Длина от- |
Каждый отрезок имеет опреде- |
|
|
|
|
резка |
ленную длину, большую нуля. |
|
|
|
|
|
Длина отрезка равна сумме |
|
|
|
|
|
длин частей, на которые он |
|
|
|
|
|
разбивается любой точкой. |
|
|
|
|
Мера угла |
Каждый угол имеет опреде- |
|
|
|
|
|
ленную меру, большую нуля. |
|
|
|
|
|
Мера угла равна сумме мер |
|
|
|
|
|
углов, на которые он разби- |
|
|
|
|
|
вается любым лучом, выходя- |
|
|
|
|
|
щим из его вершины и прохо- |
|
|
|
|
|
дящим между его сторонами. |
|
|
|
|
|
Градусная мера развернутого |
|
|
|
|
|
угла равна 180°. |
|
|
|
|
Готовимся к изучению темы |
|
|
|
|
|
|
|
|
|
|
339 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Площадь |
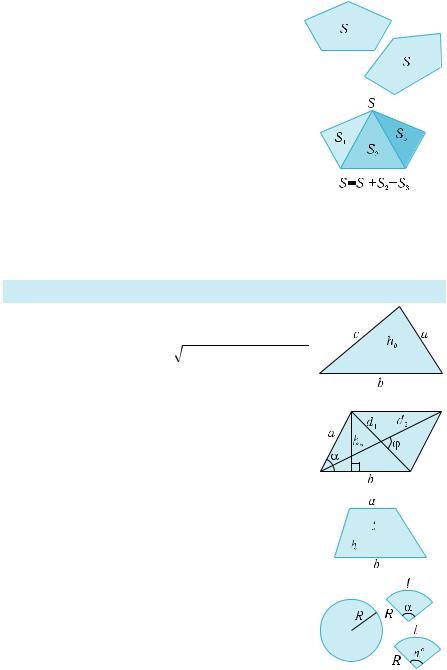
Площадь многоугольника — |
|
|
|
|
|
|
|
|
|||||||||||
|
фигуры |
это |
положительная величи- |
|
|
|
|
|
|
|
|
||||||||||
|
|
на, |
обладающая следующими |
|
|
|
|
|
|
|
|
||||||||||
|
|
свойствами |
: |
|
многоугольники |
|
|
|
|
|
|
|
|
||||||||
|
|
1) равные |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
имеют равные площади; |
|
|
|
|
|
|
|
|
|||||||||||
|
|
2) если многоугольник со- |
|
|
|
|
|
|
|
|
|||||||||||
|
|
ставлен из нескольких много |
|
|
|
|
|
|
|
|
|||||||||||
|
|
угольников, не имеющих об- |
|
|
|
|
|
|
|
|
|||||||||||
|
|
щих внутренних точек, то его |
|
|
|
|
|
|
|
|
|||||||||||
|
|
площадь равна сумме площа- |
|
|
|
|
|
|
|
|
|||||||||||
|
|
дей этих многоугольников; |
|
|
|
|
|
|
|
|
|||||||||||
|
|
3) площадь квадрата со сторо- |
|
|
|
|
|
|
|
|
|||||||||||
|
|
ной единичной длины равна |
|
|
|
|
|
|
|
|
|||||||||||
|
|
единице площади. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Площади плоских фигур |
|
|
Таблица 47 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Фигура |
|
|
Формулы площади S |
|
Рисунок |
|
||||||||||||||
|
Треугольник |
|
|
S = |
1 b hb , S = |
1 absinC, |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
R — радиус опи- |
|
|
|
|
|
|
|
|
|
|||||||||||
|
санной окружности |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
S = |
|
|
p( p − a)( p − b)( p − c), |
|
|
|
|
|
|
|
|||||||||
|
r — радиус вписан- |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ной окружности |
|
|
|
|
|
|
abc |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
р — полупериметр |
|
S = rp = |
4R . |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Параллелограмм |
|
S = b h , |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = absin α, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
S = |
1 d d sin ϕ. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
Трапеция |
|
|
|
t = a + b , |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a, b — основания |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
h — высота |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
S = t h = a + b |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
t — средняя линия |
|
h. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Круг, сектор |
|
S = πR2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
S = |
αR2 |
|
, S = |
|
πn° |
R2 . |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
360° |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
c |
|
|
2 |
|
c |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
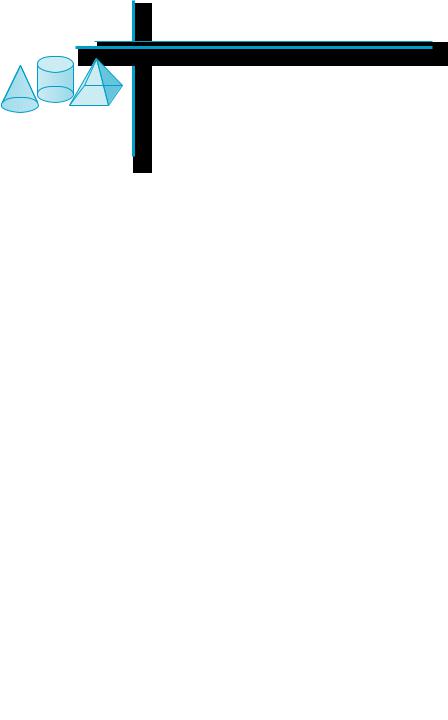
Тест для диагностики готовности к изучению темы «Объемы и площади поверхностей геометрических тел»
1.Во сколько раз нужно увеличить длины сторон квадрата, что- бы его площадь увеличилась вдвое?
|
А. В 2 раза. |
Б. В 4 раза. |
В. В |
2 раз. |
Г. В 1,5 раза. |
|
2. |
Как изменится площадь прямоугольника, если одну сторону |
|||||
|
увеличить вдвое, а вторую уменьшить вдвое? |
|
||||
|
А. Увеличится в 2 раза. |
Б. Уменьшится в 2 раза. |
||||
|
В. Увеличится в 1,5 раза. |
Г. Не изменится. |
||||
3. |
Середины сторон параллелограмма последовательно соеди- |
|||||
|
нили отрезками. Во сколько раз площадь образованного че- |
|||||
|
тырехугольника меньше площади параллелограмма? |
|||||
|
А. В 1,5 раза. |
Б. |
В 2 раза. |
В. В 3 раза. |
Г. В 4 раза. |
|
4. |
Середины сторон |
выпуклого |
четырехугольника последова- |
|||
|
тельно соединили. Полученный четырехугольник является ... |
|||||
|
А. параллелограммом. |
Б. прямоугольником. |
||||
|
В. ромбом. |
|
|
Г. трапецией. |
|
|
5. |
Середины сторон некоторого четырехугольника последова- |
|||||
|
тельно соединили. Получили ромб. Каким из следующих |
|||||
|
свойств обладает данный четырехугольник? |
|
||||
|
А. Диагонали делят углы пополам. |
|
|
|||
|
Б. Диагонали взаимно перпендикулярны. |
|
||||
|
В. Диагонали точкой пересечения делятся пополам. |
|||||
|
Г. Диагонали равны. |
|
|
|
||
6. |
В выпуклом 10-угольнике провели все диагонали. Сколько |
|||||
|
всего проведено диагоналей? |
В. 40. |
|
Г. 35. |
||
|
А. 80. |
Б. |
70. |
|
||
7. |
На гипотенузе и на катете равнобедренного прямоугольного |
|||||
|
треугольника построили квадраты. Во сколько раз площадь |
|||||
|
квадрата, построенного на гипотенузе, больше площади ква- |
|||||
|
драта, построенного на катете? |
|
|
|||
|
А. В 2 раза. |
Б. В 4 раза. |
В. В |
2 раз. |
Г. В 1,5 раза. |
|
