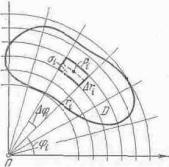
1.3. Вычисление двойных интегралов в полярных координатах

Для вычисления двойного интеграла I = ∫∫ f (x, y)dσ мы пользовались до сих пор

D

системой декартовых координат. Отнесём теперь плоскость к системе полярных координат r, φ и предположим, как обычно, что полюс лежит в начале координат и полярная ось совпадает с осью абсцисс. Тогда декартовы координаты точки выражаются через полярные по формулам

рис.15

x = r cos φ, у = r sin φ.

Разобьём область интегрирования D на частичные области σi двумя системами координатных линий: r = const, φ = const. Этими линиями будут соответственно концентрические окружности с центром в полюсе и лучи, исходящие из полюса (рис. 15). При этом частичными областями σi будут криволинейные четырехугольники, ограниченные дугами концентрических окружностей и их радиусами. Площадь σi области σi будет

Пусть дана функция f(x, у), непрерывная в области D. Составим для неё интегральную сумму, разбивая область D на частичные области σi, и выбирая в качестве произвольных точек Рi (xi , yi) областей σi точки, лежащие на средних окружностях радиуса ri т.е. полагая

Так как в правой части стоит интегральная сумма для функции f(r cos φ, r sinφ) r по переменным r и φ, то, переходя к пределу, получим

I = ∫∫ f (x, y)dxdy = ∫∫ f (r cosϕ , r sinϕ )rdrdϕ .

D D

Это равенство является формулой преобразования двойного интеграла от декартовых координат к полярным. Выражение dσ = r dr dϕ называется элементом площади в полярных координатах.

Правило преобразования двойного интеграла к полярным координатам.

Для того чтобы преобразовать двойной интеграл в декартовых координатах в двойной интеграл в полярных координатах, нужно x и у в подынтегральной функции заменить соответственно через r cos φ и r sin φ, а произведение dx dy заменить произведением r dr dφ.

49

где D – полукруг, являющийся половиной основания цилиндра.

Здесь очень удобно преобразовать двойной интеграл к полярным координатам. В

Так как полярное уравнение полуокружности, ограничивающей область D, есть r = a cos φ (см. пример 7), то, интегрируя сначала по r, а затем по φ, найдём

1.4. Приложения двойных интегралов к задачам механики

Масса плоской пластинки переменной плотности.

Рассмотрим тонкую пластинку, расположенную на плоскости Оху и занимающую область D. Толщину этой пластинки считаем настолько малой, что изменением плотности по толщине её можно пренебречь.

Поверхностной плотностью такой пластинки в данной точке называется предел отношения массы площадки к её площади при условии, что площадка стягивается к данной точке.

Определённая таким образом поверхностная плотность будет зависеть только от положения данной точки, т.е. являться функцией её координат: = δ(x, y).

Рис.19

Если бы плотность была постоянной (δ = const), то масса всей пластинки равнялась бы Μ = δ S, где S – площадь пластинки. Найдём теперь массу неоднородной пластинки, считая, что её плотность является заданной функцией δ (x, y). Для этого разобьём область, занимаемую пластинкой, на частичные области σ1, σ2, …, σn с площадями σ1 σ2 , …, σn (рис. 19). Выбирая в каждой частичной области произвольную точку Pi (xi yi), будем считать, что плотность во всех точках частичной области постоянна и равна плотности δ(xi yi) в выбранной точке. Составим приближённое выражение для массы пластинки в виде интегральной суммы

n

M n = ∑ δ ( xi , yi ) σ i i =1

51

Для точного выражения массы следует найти предел суммы при условии n → ∞ и каждая

частичная область стягивается к точке. Тогда M = ∫∫ δ ( x , y ) d σ .

D

Статические моменты и центр тяжести пластинки.

Перейдём теперь к вычислению статических моментов рассматриваемой пластинки относительно осей координат. Для этого сосредоточим в точках Pi (xi, yi) массы соответствующих частичных областей и найдём статические моменты полученной системы материальных точек:

n

M x( n ) = ∑ yiδ ( xi , yi ) σ i , i =1

n

M y( n ) = ∑ xiδ ( xi , yi ) σ i . i =1

Переходя к пределу при обычных условиях и заменяя интегральные суммы интегралами, получим

M x = ∫∫ yδ ( x, y)dδ , M у = ∫∫ xδ ( x, y )dδ

Находим координаты центра тяжести:

Если пластинка однородна, т.е. δ (x, у) = const, то формулы упрощаются :

где S – площадь пластинки.

Моменты инерции пластинки

Моментом инерции материальной точки Ρ с массой m относительно какой-либо оси называется произведение массы на квадрат расстояния точки Ρ от этой оси.

Метод составления выражений для моментов инерции пластинки относительно осей координат совершенно такой же, какой мы применяли для вычисления статических моментов. Приведём поэтому только окончательные результаты, считая, что δ(х, у) =1.

Отметим еще, что интеграл ∫∫ xyd σ называется центробежным моментом инерции; он

D

обозначается Ιxy.

В механике часто рассматривают полярный момент инерции точки, равный произведению массы точки на квадрат ее расстояния до данной точки – полюса. Полярный момент инерции пластинки относительно начала координат будет равен

I0 = ∫∫(x2 + y 2 )dσ = I x + I y .

D

52