
- •1. Дифференциальные уравнения I порядка. Уравнения с разделяющимися переменными
- •1.1. Дифференциальные уравнения I порядка. Общие понятия
- •1.2. Дифференциальные уравнения с разделяющимися переменными
- •2. Однородные дифференциальные уравнения. Уравнения в полных дифференциалах
- •2.1. Однородные дифференциальные уравнения I порядка
- •2.2. Уравнения в полных дифференциалах
- •3.2. Уравнения Бернулли
- •5.2. Неоднородные линейные уравнения ІІ порядка с постоянными коэффициентами. Метод Эйлера вариации произвольных постоянных
- •6. Линейные неоднородные уравнения ІІ порядка с постоянными коэффициентами. Метод Лагранжа неопределенных коэффициентов
- •7. Системы дифференциальных уравнений
- •7.1 Нормальная система дифференциальных уравнений
- •Модуль 10. Кратные интегралы
- •1. Двойной интеграл
- •1.1. Объём цилиндрического тела
- •1.2. Вычисление двойных интегралов в декартовых координатах
- •1.3. Вычисление двойных интегралов в полярных координатах
- •1.4. Приложения двойных интегралов к задачам механики
- •1.5. Вычисление площадей и объёмов с помощью двойных интегралов.
- •1.6. Вычисление площади поверхности.
- •2. Тройной интеграл
- •2.1. Масса неоднородного тела
- •2.2. Вычисление тройных интегралов в декартовых координатах.
- •2.3. Вычисления тройных интегралов в цилиндрических координатах.
- •2.4. Вычисление тройных интегралов в сферических координатах
- •2.5. Приложение тройных интегралов.
- •Модуль 11. Криволинейные и поверхностные интегралы
- •1. Криволинейные интегралы
- •1.1. Криволинейный интеграл первого типа (по длине дуги)
- •1.3. Формула Грина
- •1.4. Условия независимости криволинейного интеграла от пути интегрирования
- •1.5. Связь между криволинейными интегралами первого и второго типов
- •2. Поверхностные интегралы
- •2.1. Поверхностные интегралы первого типа
- •2.2. Понятие двухсторонней поверхности. Ориентация поверхности
- •2.3. Поверхностный интеграл второго типа (по проекциям)
- •2.4. Связь поверхностных интегралов I и II типов
- •2.5. Формула Остроградского
- •3. Основные понятия теории поля
- •Список литературы
Модуль 11. Криволинейные и поверхностные интегралы
1. Криволинейные интегралы
1.1. Криволинейный интеграл первого типа (по длине дуги)
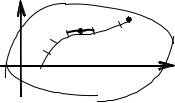
Пусть в некоторой области D плоскости хоу (см. рис. 1) задана непрерывная функция f(x, y) и гладкая незамкнутая кривая L между точками А, В.
y
Mi B
Ai−1 Ai
D
A 
Рис..1
Составим интегральную сумму по уже известному алгоритму. Разобьём кривую L точками
А = А0, А1, ..., Ап = В
на п произвольных участков li, обозначив через li длину i–го участка кривой между точками
Аi−1, Ai, где I = 1, 2, …,п.
В каждом i-том участке выберем произвольно точку Mi = (ξi, ηi) и подсчитаем в ней значение функции fi = f(Mi).
Просуммировав произведения fi li по всем i = 1, 2, …, п, получим интегральную сумму
n |
n |
∑fi |
l i = ∑f (ξ i , ηi ) l i . |
i = 1 |
i = 1 |
Предел этой интегральной суммы, если он существует и не зависит от типа разбиения дуги L и способа нахождения точек Mi, где i = 1, 2, …, п, называется криволинейным интегралом первого типа от функции f(x, y), взятым по кривой L, и обозначается
lim |
n |
f (M |
i |
) |
l |
i |
= |
∫ |
f (x, y)dl , где d = max l |
. |
d → 0 |
∑ |
|
|
|
|
i |
|
|||
(n → ∞) i = 1 |
|
|
|
|
|
|
L |
|
|
|
Этому интегралу можно придать вполне определённый физический смысл: если в каждой точке дуги L задана переменная плотность μ(х, у) — функция точки, то можно подсчитать массу материальной дуги АВ: m = ∫ μ (x, y)dl .
L
Сравните с задачей о вычислении массы неоднородного стержня, приводящей к понятию определённого интеграла (см. [3]).
Основные свойства криволинейного интеграла первого типа
•Криволинейный интеграл первого типа не зависит от направления пути интегрирования:
∫f (M )dl = ∫ f (M )dl .
AB |
BA |
• Интеграл от суммы (разности) функций равен сумме (разности) интегралов от каждого слагаемого по тому же пути интегрирования:
∫ [f1 (M ) ± f2 (M )]dl = ∫ f1 (M )dl ± ∫ f2 (M )dl .
L L L
• Константа выносится за знак интеграла:
∫ cf (M )dl |
= c∫ f (M )dl , где c = const . |
L |
L |
65
• Свойство аддитивности: если путь интегрирования L разбить на участки L1, L2 …, Ln, то интеграл по всей дуге равен сумме интегралов по участкам Li, где i = 1, 2, …, n:
∫ f (M )dl = ∫ f (M )dl + ∫ f (M )dl + + ∫ f (M )dl .
L L1 L2 Ln
•Формула для вычисления длины дуги (если f(М) = 1 для всех точек кривой L):
∫dl = l, где l — длина дуги L.
L
Как вычислить криволинейный интеграл?
Представим уравнение кривой L в параметрической форме
L : x |
= ϕ(t ), |
(t 0 ≤ t ≤ T ). |
y |
= ψ(t ) |
|
Направление установлено произвольно (одно из двух возможных). Функции ϕ(t ), ψ(t ) непрерывны вместе со своими производными ϕ′, ψ′ . Функция f(x, y), определённая в каждой точке кривой, сводится к функции одной переменной t:
f (x, y) = f [ϕ(t ), ψ(t )]. |
|
|
|
′ |
2 |
′ |
2 |
Дифференциал дуги вычисляем по формуле dl = (ϕt |
) |
+ (ψ t |
) dt . |
Записываем формулу для вычисления криволинейного интеграла
|
T |
|
|
|
|
∫ f (x, y)dl = ∫ f [ϕ(t ), ψ(t )] |
′ |
2 |
′ |
2 |
|
(ϕt |
) |
+ (ψ t |
) dt , |
||
L |
t0 |
|
|
|
|
где правая часть равенства — определённый интеграл по переменной t. В случае пространственной кривой
x |
= x(t ), |
|
2 |
|
2 |
|
2 |
|
|
′ |
′ |
′ |
|||
L : y = y(t ), |
|
|
|
||||
dl = (x (t )) |
+ [y (t )] |
+ [z (t )] dt , |
|||||
z |
= z(t ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
T |
|
f (x, y, z)dl |
= |
∫ |
f [x(t ), y(t ), z(t )] (x t′ )2 + (yt′ )2 + (zt′ )2 dt . |
|
|
|
|||
L |
|
|
t0 |
|
Таким образом, чтобы вычислить криволинейный интеграл по кривой L от функции f(x, y), необходимо свести его к определённому интегралу по аргументу t. Для этого уравнение линии L записывают в параметрической форме и переводят всё подынтегральное выражение к выбранной переменной, начальное и конечное значения которой соответствуют начальной и конечной точкам дуги L выбранного направления; дифференциал dl подсчитывают по формуле
(2). В случае трёхмерного пространства используют формулы (3) – (4).
Пример 1. Вычислить массу неоднородной дуги АВ: у2 = 2х с плотностью μ = yx ,
A (1,  2 ), B(2, 2) .
2 ), B(2, 2) .
Решение. Запишем уравнение АВ в параметрическом виде.
Пусть у = t. Тогда x = |
t 2 |
, |
2 ≤ t ≤ 2 |
(y |
A |
= t |
A |
= |
2, y |
B |
= t |
B |
= 2). |
|||
|
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Функция μ(х, у) примет вид μ = |
t 2 |
= |
|
t |
. |
|
|
|
|
|
|
|
|
|||
2 t |
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдём dl: yt′ = 1, x t′ = 21 2t |
= t, |
dl |
= |
|
t 2 |
+ 1dt . |
|
|
|
|
|
|||||
Вычислим искомую массу по формуле (13.1):
66
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
2 |
|
1 |
|
|
2 |
|
(t 2 + 1)2 |
|
|
|
||
m =∫ μ dl = ∫ 2t t |
+ 1 dt |
= 14 ∫ |
(t |
+ 1)2 d(t |
+ 1) = 14 |
|
|
= |
|||||||||
|
|
|
3 |
|
|
||||||||||||
L |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
Пример 2. Вычислить ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2x 2 |
+ y 2 dl , |
где L – линия пересечения поверхностей |
|||||||||||||||
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 + y 2 + z2 = R 2 , z = x.
Решение. Кривая представляет собой пересечение сферы и плоскости – это окружность
(см. рис. 2).
В качестве параметра выберем х = t. Из равенства z = х следует z = t. Из уравнения сферы найдём у:
z R
R y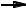
x
Рис..2
y 2 = R 2 − 2t 2 , y = ±  R 2 − 2t 2 .
R 2 − 2t 2 .
Итак, параметрические уравнения линии интегрирования L:
x = t , z = t ,
y = ± R 2 − 2t 2 .
R 2 − 2t 2 .
Пределы интегрирования по аргументу t находим из условия существования функции у:
R |
2 |
− 2t |
2 |
≥ 0, |
t |
2 |
≤ |
R2 |
, |
|
t |
|
≤ |
R |
, − |
R |
≤ t ≤ |
R |
. |
|
|
||||||||||||||||||
|
|
|
2 |
|
|
2 |
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составляем дифференциал дуги по формуле (3), для чего найдём производные
′ |
′ |
′ |
|
2t |
; |
|
|
||||
x (t ) = 1, z (t ) = 1, y (t ) = |
|
R 2 − 2t 2 |
|||
|
|
|
|
|
|
|
|
4t 2 |
|
2Rdt |
|
dl = |
1 + 1 + |
R 2 − 2t 2 dt = |
R 2 − 2t 2 . |
|
|
Подынтегральная функция примет вид
2x 2 + y 2 =  2t 2 + R 2 − 2t 2 = R .
2t 2 + R 2 − 2t 2 = R .
Переводим криволинейный интеграл в определённый по формуле (4) и вычисляем его:
|
|
|
|
|
R |
2 |
|
|
|
R |
2 |
|
|
|
|
||
∫ 2x 2 + y 2 dl = ∫ |
|
dt |
= R 2 ∫ |
|
dt |
||||||||||||
|
2R 2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
= |
||||||||||
|
R 2 − 2t 2 |
|
|
R2 |
− t 2 |
||||||||||||
L |
|
|
|
− R |
2 |
|
|
|
− R |
2 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
||
= |
R 2 arcsin |
2t |
2 |
|
|
= R 2 π. |
|
|
|
|
|
|
|
|
|||
R |
− |
R |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 3. Найти длину астроиды x |
= a cos3 t, |
y |
= a sin 3 t. |
||||||||||||||
Решение. Воспользуемся формулой l = ∫ dl . |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
В нашем случае |
|
|
|
|
|
|
|
|
|
|
|||||||
x ′ |
= −3a cos2 t sin t, |
y ′ = 3a sin 2 t cos t, |
|
|
|
|
|
||||||||||
t |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
dl |
= 3a cos4 t sin 2 t |
+ sin 4 t cos2 t dt = = 3a cos t sin t cos2 t + sin 2 t dt = 3 a sin 2tdt . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Поскольку кривая симметрична относительно осей координат, то
67
π2 |
3 |
|
|
|
|
|
|
|
cos2t |
π 2 |
|
|
|
|
|
|
|
|
||
l = 4 ∫ |
|
a sin 2tdt |
= 6a − |
2 |
|
|
|
= 6a. |
|
|
|
|||||||||
2 |
0 |
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 4. Вычислить массу лемнискаты (x 2 |
+ y 2 )2 = 2a2 xy (см. рис. 3) с плотностью в |
|||||||||||||||||||
каждой точке, равной расстоянию её до начала координат. |
||||||||||||||||||||
Решение. В нашем случае |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
m = ∫ μ(x, y)dl = ∫ x 2 + y 2 dl . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
L |
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для вычисления интеграла удобнее воспользоваться полярными координатами, где |
||||||||||||||||||||
x = ρ cos ϕ, |
y = ρ sin ϕ, |
|
dl |
= ρ |
2 |
|
|
|
′ |
2 |
dϕ. |
|
|
|||||||
|
|
+ (ρ ϕ ) |
|
|
||||||||||||||||
Тогда функция плотности μ = |
x 2 |
+ y 2 |
= ρ, уравнение кривой примет вид |
|||||||||||||||||
(ρ2 cos2 ϕ + ρ2 sin 2 ϕ)2 |
= 2a2ρ2 cos ϕ sin ϕ, |
|
|
|
||||||||||||||||
ρ2 = a2 sin 2ϕ, ρ = a sin 2ϕ , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
π/2 |
|
|
|
π |
|
|
|
ρ′ |
= |
|
|
|
a |
|
|
2 cos2ϕ; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
/4 |
|
|
|
|
ϕ |
|
2 |
|
sin 2ϕ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
dl = ρ |
2 |
+ |
′ |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
(ρ ϕ ) |
dϕ = |
|||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
cos2 |
2ϕ |
|
|
|
|
|
|
|
|
|
a2 sin 2ϕ + |
|
dϕ = |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2ϕ |
|||||
|
|
|
|
= |
|
a |
|
|
dϕ, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
sin 2ϕ |
|
|
|
|
|
||||
или dl |
= |
|
a2 |
|
dϕ = |
|
a2 |
dϕ. |
|
|
|
|
|
|
|
|
|
|
|
|
a |
sin 2ϕ |
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теперь запишем полностью интеграл, используя симметрию кривой:
π |
|
|
π |
m = 2 ∫2 |
ρ |
a2 |
dϕ = 2a2 ∫2dϕ = 2a2 [ϕ]0π2 = πa2 . |
ρ |
|||
0 |
0 |
||
1.2.Криволинейный интеграл второго типа (по координатам)
Впространственной области Т рассмотрим три функции P(x, y, z), Q(x, y, z), R(x, y, z), непрерывные на дуге АВ кусочно-гладкой кривой L.
Разобьём дугу АВ точками Mi(xi, yi, zi) на п элементарных дуг Mi−1Mi (i = 1, 2, …, n), на каждой из которых произвольно выберем точку Ki. Вычислим значения каждой из функций в выбранных точках
P(K i ), Q(K i ), R(K i ), где i = 1, 2, …, n.
Спроектируем каждую элементарную дугу на оси координат, обозначив их проекции
соответственно |
xi, yi, |
zi. Составим произведения |
P(K i ) x i , Q(K i ) y i , |
R(K i ) zi |
|
для всех i = 1, 2, …, n и просуммируем их: |
||
n |
|
|
Sn = ∑[P(K i |
) x i + Q(K i ) y i + R(K i ) zi ], |
|
i = 1 |
|
|
где Sn— интегральная сумма для функций P, Q, R.
68

Определение. Криволинейным интегралом второго типа, взятым по кривой L (или по пути АВ), называется предел интегральной суммы Sn при п → ∞ и
max x i → 0, max y i → 0, max zi → 0.
Обозначается: lim S |
n |
= |
∫ |
P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz. |
n → ∞ |
|
|
||
|
|
|
L |
|
Вчастности, в двухмерном пространстве, если кривая L целиком находится в плоскости хоу,
афункции P, Q, R не зависят от переменной z, имеем криволинейный интеграл
∫ P(x, y )dx + Q(x, y )dy =
L
lim
max xi max yi
n
→ 0 ∑[P(K i ) x i + Q(K i ) y i ].
→ 0 i = 1
Докажем, что составной интеграл существует, и одновременно получим метод его вычисления.
Теорема 1 (существования). Если АВ — дуга кусочно-гладкой кривой L и функции P(x, y, z), Q(x, y, z), R(x, y, z) определены на дуге АВ, то предел интегральной суммы Sn существует и не зависит ни от способа деления дуги АВ на части, ни от выбора точек Ki на каждой из элементарных дуг.
Доказательство. Разобьём правую часть формулы (5) на составные однотипные суммы, обозначив
Sn, x
Sn, y
Sn, z
n
= ∑ P(K i ) x i ,
i = 1
n
= ∑Q(K i ) y i ,
i= 1 n
=∑R(K i ) zi .
i= 1
Рассмотрим первую из них. Перепишем уравнение кривой L в параметрическом виде
L : x = x (t ), y = y(t ), z = z(t ).
Тогда точке Mi−1 соответствует значение параметра ti−1, точке Ki — значение t~i , точке Mi — значение ti, т.е. каждой точке
кривой L соответствует определённое значение параметра t. Подставим формулы (8) в интегральную сумму
Sn, x = ∑n |
P[x (t~i ), y (t~i ), z(t~i ) ](x i − x i − 1 ), |
|
|
|
|
||||
i = 1 |
|
|
|
|
|
|
|
|
|
где xi = x(ti), xi−1 = x(ti−1). |
|
|
|
|
|
|
|
||
По теореме Лагранжа x i |
− x i − |
|
′ |
|
t i |
, |
|
||
1 = x (θi ) |
|
||||||||
где t i − 1 < θi < t i , |
t i = t i − t i − 1. |
|
|
|
|
||||
Представим x ′(θi ) = x ′(t~i |
) + α i , |
где αi − бесконечно малая (в силу непрерывности |
|||||||
|
′ |
→ 0 при |
t i |
→ 0 ). |
|
|
|
||
производной x (t ), α i |
|
|
|
||||||
По условию кривая L – кусочно-гладкая, т.е. обладает непрерывно изменяющейся |
|||||||||
касательной, а это означает, что |
′ |
′ |
|
′ |
|
||||
x |
(t ), y |
(t ), |
z (t ) — непрерывные функции. |
|
|||||
|
n |
|
(t~i ), z(t~i |
)]x ′(t~i |
) |
|
n |
) t i . |
|
Тогда Sn, x = ∑ P[x (t~i ), y |
t i |
+ + ∑ P[x (t~i ), y (t~i ), z(t~i )]α i ( t i |
|||||||
|
i =1 |
|
|
|
|
|
|
i = 1 |
|
Первое слагаемое в правой части равенства является интегральной суммой для функции одной переменной
69
P(x, y, z)x ′(t ) = P[x (t ), y(t ), z(t )]x ′(t )
и поэтому (см. [3]) имеет своим пределом определённый интеграл
tB |
|
′ |
∫ |
P[x(t), y(t), z(t)]x (t) dt = lim Sn,x . |
|
tA |
n→ ∞ |
|
|
||
Второе слагаемое суммы Sn,x имеет своим пределом ноль как бесконечно малая высшего порядка по сравнению с ti.
Аналогично доказываем существование пределов двух последних сумм формул
Делаем вывод: составная интегральная сумма имеет конечный предел, равный сумме трёх слагаемых:
lim |
Sn = |
t B |
P[x (t ), y(t ), z(t )]x (t )dt + |
t B |
Q[x (t ), y(t ), z(t )]y (t )dt + + |
t B |
R[x (t ), y(t ), z(t )]z (t )dt , |
|||||
∫ |
∫ |
∫ |
||||||||||
|
|
|
|
|
|
′ |
′ |
′ |
||||
max |
|
|
tk |
|
→ 0 |
|
|
|
||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
t A |
|
t A |
|
t A |
|
|
где tA — значение параметра в точке А (начале пути интегрирования), tB — значение параметра в точке B (конце пути интегрирования).
|
t |
∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz = = ∫B P[x (t ), y(t ), z(t )]x t′ (t )dt + Q[x (t ), y(t ), z(t )]yt′ (t )dt + |
|
AB |
t A |
+ R[x (t ), y(t ), z(t )]zt′ (t )dt . |
|
Таким образом, мы не только доказали факт существования криволинейного интеграла, но и получили метод его вычисления, а именно: чтобы вычислить интеграл второго типа, его необходимо перевести в определённый интеграл по формуле (10), выразив переменные х, у, z через параметр t, выбранный на линии интегрирования
L : x = x (t ), y = y(t ), z = z(t ),
соответственно заменив дифференциалы
′ |
′ |
′ |
dx = x (t )dt , |
dy = y (t )dt , |
dz = z (t )dt . |
Криволинейному интегралу (в механике и физике его называют линейным) можно придать вполне определённый физический смысл: как работы переменной силы
F {P, Q, R}
вдоль кривой L от точки А до точки В. Вспомним начальные сведения о работе:
• сила F — постоянный вектор,
путь S — прямолинейный отрезок,
работа равняется скалярному произведению: A = F S ;
•работа переменной силы на прямолинейном участке вычисляется с помощью определённого интеграла от модуля силы;
•работа переменной силы
F = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k ,
изменяющейся от точки к точке (в этом случае пространство Охуz называется силовым векторным полем), по перемещению материальной точки по дуге АВ вычисляется с помощью криволинейного интеграла по формуле
A = ∫ |
|
dl |
|
= |
∫ Pdx + Qdy + Rdz, |
F |
|
||||
AB |
AB |
||||
где dl = i dx + j dy + k dz.
70

Свойства криволинейного интеграла
1. При изменении направления дуги АВ на противоположное криволинейный интеграл меняет свой знак, сохраняя абсолютную величину:
∫ Pdx + Qdy + Rdz = − ∫ Pdx + Qdy + Rdz.
AB BA
Действительно, все слагаемые интегральной суммы (5), пределом которой является линейный интеграл, изменят свой знак на противоположный, т.е. криволинейный интеграл второго типа является ориентированным.
2. Составной интеграл (6) равен сумме трёх простых линейных интегралов
∫ Pdx + Qdy + Rdz = |
∫ Pdx + ∫ Qdy + ∫ Rdz. |
||
AB |
AB |
AB |
AB |
Мы пользовались этим свойством при доказательстве теоремы существования (см. формулы
(7)).
3. Если дугу АВ разбить точками А1, А2, …, Аk на конечное число составляющих дуг (см. рис. 4), то криволинейный интеграл по кривой АВ равен сумме интегралов по составляющим дугам (свойство аддитивности), т.е.
∫ = ∫ + |
∫ + |
+ ∫ . |
AB AA 1 |
A1A2 |
Ak B |
В механике и физике такой интеграл носит название циркуляции вектора
F {P( x , y, z), Q( z, y, z), R( x , y, z)} вдоль замкнутого контура L (
При этом ориентация контура считается положительной, когда обход контура происходит против часовой стрелки. Если в условии задачи ничего не говорится о направлении обхода контура, он предполагается положительным.
Замечание 2. В двухмерном пространстве, в частности на плоскости хоу, путь интегрирования АВ обычно задаётся функцией у =f(x). В качестве параметра в этом случае удобно взять независимую переменную х. Тогда параметрические уравнения кривой будут x = x, у =f(x), где х1 < x < x2 при условии, что координаты точек А(х1, у1), В(х2, у2) известны. В противном случае их надо найти согласно условию задачи. Формула (10) в этой ситуации примет вид
x2
∫P(x , y )dx + Q(x , y )dy = ∫ P[x , f (x )]dx + Q[x , f (x )]f ′(x )dx .
AB |
x1 |
В частности,
x2
∫P(x, y)dx = ∫ P[x, f (x )]dx.
AB |
x1 |
Пример 5. Вычислить ∫(x − y)dx + (x + y)dy , где L — эллипс ax22 +
L
против часовой стрелки (обозначать этот факт можно знаком L+). Решение. Запишем уравнение эллипса в параметрической форме
x = a cos t, y = b sin t, где 0 ≤ t ≤ 2π.
Найдём дифференциалы для каждой переменной: dx = –asintdt, dy = bcostdt.
Перейдём к определённому интегралу и вычислим его:
y2 = 1 , пробегаемый
b2
71
∫ ( x − y) dx + ( x + y) dy =
L+
= |
2∫π (acost − bsin t )(− asin t )dt |
+ (acost + bsin t ) bcostdt = |
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
2π |
2π |
|
|
|
|
|
|
|
= (b2 − a2 )∫sin t costdt |
+ ab |
∫(sin 2 t + cos2 t )dt |
= |
|
|
||||
|
0 |
|
0 |
|
|
|
|
|
|
|
2π |
2π |
|
|
|
2π |
|||
|
|
|
|
||||||
= (b2 |
− a2 )∫ sin td sin t + ab ∫ dt |
= (b2 − a2 )sin22 |
t |
|
0 |
+ abt |
|
20π = 2πab. |
|
|
|
||||||||
|
|
||||||||
|
|
|
|
||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 6. Вычислить ∫ (x 2 − y )dx + (x + y)dy, где L — контур треугольника с вершинами
L+
О(0, 0), А(1, 0), В(0, 1).
Решение. Построим треугольник и воспользуемся свойством аддитивности, разбив кусочногладкий контур L на участки ОА, АВ, ВО. На каждом из них укажем направление интегрирования (см. рис 5).
Символически интеграл можно записать в виде трёх слагаемых:
∫ = ∫ + ∫ + ∫.
L+ OA AB BO
y
B(0, 1)
O |
A(1, 0) x |
Рис..5
Подготовим параметрическую запись каждого из линейных участков:
•ОА — это часть оси Ох (уравнение которой у = 0), где изменяется только переменная х, её
ивозьмём в качестве параметра. Тогда
у = 0, х = t, где t0 = 0, tA = 1, dy = 0, dx = dt;
• АВ — прямая, отсекающая равные отрезки на осях координат. Используя уравнение ax + by = 1 , имеем х + у = 1.
Пусть х = t, тогда у = 1 − t, где tA = 1, tB = 0, соответственно dx = dt, dy = − dt;
• BO — участок оси Оу, т.е. у — изменяющаяся переменная, её и возьмём в качестве параметра. Тогда
y = t, x = 0, где tB = 1, tО = 0; dy = dt, dx = 0.
Вычисляем криволинейный интеграл, записав его в виде суммы определённых интегралов:
∫ (x 2 − y )dx + (x + y)dy = ∫ (x 2 − y )dx + (x + y)dy +
L+ OA
+ ∫ (x 2 − y )dx + (x + y)dy + ∫ (x 2 − y )dx + (x + y)dy =
AB BO
72

= ∫1 t 2 dt + ∫0 [(t 2 − 1 + t )dt − dt ]+ ∫0 tdt .
0 |
1 |
1 |
Изменив у первого интеграла ориентацию, получим все слагаемые с одинаковыми пределами:
0 |
2 |
|
2 |
|
|
0 |
|
(t − 1)2 |
|
0 |
|
|
|
|
|
|
|
||||||
∫ =∫ (− t |
|
+ t |
|
− 1 |
+ t − 1 + t )dt = 2∫ (t − 1)dt = |
2 |
|
|
|
= 1. |
|
|
|
2 |
|
1 |
|||||||
L 1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 7. Вычислить ∫ (y 2 |
+ 3z2 )dx + 2yzdy |
− 2x 2 dz, где L — линия пересечения |
|||||||||
L
поверхностей y = x2 и z = xy от точки О(0, 0, 0) до точки A(2, 4, 8).
Решение. Запишем уравнения линии L в параметрической форме: пусть х = t, тогда у = t2, z = t3, где t0 = x0 = 0, tA = xA = 2.
Приведём криволинейный интеграл к определённому, используя параметрическое задание кривой, предварительно найдём дифференциалы:
dx = dt, dy = 2tdt, dz = 3t2dt;
∫ (y 2 + 3z2 )dx + 2yzdy |
− 2x 2 dz = = ∫2 |
(t 4 |
+ 3t 6 )dt + 2t 2 t 3 2tdt − 2t 2 3t 2 dt =∫2 |
(7t 6 − 5t 4 )dt = |
L |
0 |
|
0 |
|
= [t 6 − t 5 ]2 = 64 − 32 = 32. |
|
|
|
|
0 |
|
|
|
|
Пример 8. Вычислить интеграл ∫ xdx |
+ ydy + (x + y − 5)dz, где L — отрезок прямой от точки |
|||
|
L |
|
|
|
(1, 1, 1) до точки (2, 3, 4).
Решение. Найдём уравнение пути интегрирования как уравнение прямой, проходящей через две заданные точки
x − x1 |
= |
y − y1 |
= |
z − z1 |
, |
x 2 − x1 |
y 2 − y1 |
|
|||
|
|
z2 − z1 |
|||
которое затем перепишем в параметрическом виде
x − 1 |
= |
y − 1 |
= |
z − 1 |
|
x − 1 |
= |
y − 1 |
= |
z − 1 |
= t, |
|
2 − 1 |
3 − 1 |
4 − 1 |
1 |
2 |
3 |
|||||||
|
|
|
|
|
|
х = t + 1, y = 2t + 1, z = 3t + 1,
где начальное значение параметра t = 0 соответствует точке (1, 1, 1), а конечное значение параметра t = 1 соответствует точке (2, 3, 4).
Дифференцируем параметрические соотношения dx = dt, dy = 2dt, dz = 3dt.
Подготовительный этап на этом заканчивается. Приступаем к вычислению криволинейного интеграла, переведя его в определённый интеграл:
∫1 [(t + 1)dt + (2t + 1)2dt + (t + 1 + 2t + 1 − 5)3dt ] =
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t + 1)2 |
|
(2t + 1)2 |
|
9(t − 1)2 |
|
1 |
|
9 |
|
1 |
|
1 |
|
9 |
|
= |
|
|
+ |
|
+ |
|
|
|
= 2 + |
|
− |
|
− |
|
− |
|
= 1. |
2 |
2 |
2 |
|
2 |
2 |
2 |
2 |
||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
73
