
- •1. Дифференциальные уравнения I порядка. Уравнения с разделяющимися переменными
- •1.1. Дифференциальные уравнения I порядка. Общие понятия
- •1.2. Дифференциальные уравнения с разделяющимися переменными
- •2. Однородные дифференциальные уравнения. Уравнения в полных дифференциалах
- •2.1. Однородные дифференциальные уравнения I порядка
- •2.2. Уравнения в полных дифференциалах
- •3.2. Уравнения Бернулли
- •5.2. Неоднородные линейные уравнения ІІ порядка с постоянными коэффициентами. Метод Эйлера вариации произвольных постоянных
- •6. Линейные неоднородные уравнения ІІ порядка с постоянными коэффициентами. Метод Лагранжа неопределенных коэффициентов
- •7. Системы дифференциальных уравнений
- •7.1 Нормальная система дифференциальных уравнений
- •Модуль 10. Кратные интегралы
- •1. Двойной интеграл
- •1.1. Объём цилиндрического тела
- •1.2. Вычисление двойных интегралов в декартовых координатах
- •1.3. Вычисление двойных интегралов в полярных координатах
- •1.4. Приложения двойных интегралов к задачам механики
- •1.5. Вычисление площадей и объёмов с помощью двойных интегралов.
- •1.6. Вычисление площади поверхности.
- •2. Тройной интеграл
- •2.1. Масса неоднородного тела
- •2.2. Вычисление тройных интегралов в декартовых координатах.
- •2.3. Вычисления тройных интегралов в цилиндрических координатах.
- •2.4. Вычисление тройных интегралов в сферических координатах
- •2.5. Приложение тройных интегралов.
- •Модуль 11. Криволинейные и поверхностные интегралы
- •1. Криволинейные интегралы
- •1.1. Криволинейный интеграл первого типа (по длине дуги)
- •1.3. Формула Грина
- •1.4. Условия независимости криволинейного интеграла от пути интегрирования
- •1.5. Связь между криволинейными интегралами первого и второго типов
- •2. Поверхностные интегралы
- •2.1. Поверхностные интегралы первого типа
- •2.2. Понятие двухсторонней поверхности. Ориентация поверхности
- •2.3. Поверхностный интеграл второго типа (по проекциям)
- •2.4. Связь поверхностных интегралов I и II типов
- •2.5. Формула Остроградского
- •3. Основные понятия теории поля
- •Список литературы

3.Основные понятия теории поля
1. Основные положения поля
Определение 1. Физическим полем называется часть пространства, в котором протекает какое-либо физическое явление.
Определение 2. Поле, в каждой точке которого определена скалярная функция U(M) = U(x, y, z) координат этой точки, называется скалярным.
Определение 3. Поле называется векторным, если в каждой его точке М(х, у, z) задан вектор
F (M ) = P(M )i + Q(M )j + R(M )k ,
где P(x, y, z), Q(x, y, z), R(x, y, z) — скалярные функции координат точки М. Примерами скалярных полей служат поле давления, поле температур
Векторными полями являются поле магнитной напряжённости, поле скоростей (жидкости, газа); поле сил тяготения, в котором каждой точке пространства ставится в соответствие сила тяжести единичной массы, помещённой в эту точку.
Если скалярная функция времени t, физическое поле называется стационарным.
U или вектор F зависят не только от координат точки, но и от называется нестационарным. Поле, не меняющееся со временем,
В дальнейшем мы будем рассматривать только стационарные поля. Графическое изображение скалярного поля Пусть скалярное поле задано функцией координат точки М
U = U(x, y, z) = U(M).
Рассмотрим те точки поля, в которых функция U(x, y, z) принимает равные значения. Физическое явление в таких точках протекает одинаковым образом.
Полагая U(x, y, z) = с, где c = const, получим уравнение некоторой поверхности. При произвольных значениях с будем иметь семейство таких поверхностей.
Определение 4. Поверхность, в каждой точке которой физическое явление протекает одинаково, называется поверхностью уровня, или эквипотенциальной поверхностью, или поверхностью равного уровня.
Если функция U(x, y, z) однозначна, то эквипотенциальные поверхности не пересекают друг друга, т.е. через каждую точку поля проходит только одна поверхность.
Пример 1. Потенциал электростатического поля задаётся функцией ϕ = qr , где q —заряд, r = x 2 + y 2 + z2 — расстояние от заряда до точки М.
Эквипотенциальная поверхность
ϕ = const, qr = c, или r 2 = (qc )2 x2 + y2 + z2 = (qc )2 .
Последнее уравнение суть сфера радиуса |
R = q |
с центром в точке приложения заряда, |
||||
|
c |
|
|
|
|
|
которую располагаем в начале координат. Так как функция ϕ = |
|
q |
однозначна, через |
|||
x 2 |
+ y 2 + z2 |
|||||
|
|
|
|
|||
каждую точку поля проходит одна поверхность уровня.
Скалярное поле, образованное функцией двух переменных, называется плоскопараллельным. Поверхностями уровня в этом случае будут цилиндрические поверхности c = f(x, y) с направляющими линиями, расположенными в плоскости хоу. Эти линии могут служить геометрическим изображением плоскопараллельного поля.
100

Например, для функции f(x, y) = x2 − y2 это будут линии x2 − y2 = c (см. рис.1). Эти линии — гиперболы, заполняющие всю плоскость. Семейство поверхностей равного уровня даёт
наглядное представление о скорости изменения поля: на участках поля, где поверхности располагаются близко друг от друга, скорость изменения поля будет больше, чем там, где эти поверхности располагаются дальше друг от друга. Так, на
рис. 1. видно, что скорость изменения плоского поля
f(x, y) = x2 − y2 в точках, близких к асимптотам, больше, чем в точках, расположенных у координатных осей
Графическое изображение векторного поля Пусть векторное поле задано векторной функцией
F (M ) = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k .
Изобразить графически это поле можно с помощью
векторных линий.
Определение 5. Векторной линией в поле вектора F называется линия, касательным вектором к которой в каждой её точке М служит вектор F (M ) (см. рис. 2).
Например, векторными линиями в поле линейных скоростей стационарного потока жидкости являются линии тока жидкости; в магнитном поле – магнитные силовые линии.
Кроме векторных линий, при изучении векторных полей используются также векторные поверхности и векторные трубки (рис. 3.).
F F
L
Рис. 2 |
Рис.3 |
Определение 6. Векторной поверхностью называется поверхность, состоящая из векторных линий, проведённых через каждую точку некоторой линии L. В случае замкнутой линии L векторная поверхность называется векторной трубкой.
Векторные линии характеризуют только направление поля. Через каждую точку поля вектора F (M ) = {P(M ), Q(M ), R(M )} проходит по одной векторной линии. Дифференциальные
уравнения векторных линий записываются в виде
dx |
|
dy |
|
dz |
|
|
= |
|
= |
|
. |
P(x,y,z) |
Q(x,y,z) |
R(x,y,z) |
|||
2. Производная скалярного поля
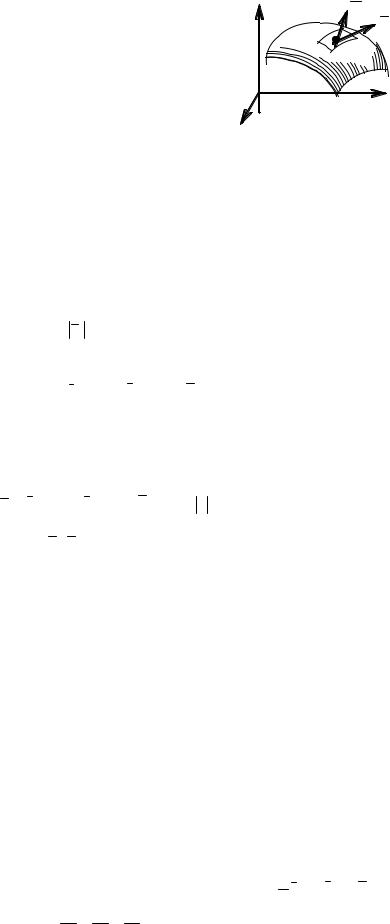
Пусть функция u(M ) = u(x, y, z) задаёт скалярное поле в некоторой области V. Выберем в этой области произвольное направление l . Задать его можно единичным вектором (см. рис..4)
l 0 |
= i |
cos α + j cos β + k cos γ |
z |
z1 |
M |
|
|
|
|
γ |
l |
|
|
|
|
α |
β |
|
M0 |
y1 |
0 |
|
y |
x |
|
Рис.4 |
|
|
l 0 = 1.
На l выберем две точки M0 и М, тогда можно говорить о приращении функции
u = u(M ) − u(M 0 ) .
Оно определяет изменение поля при переходе от точки M0 к точке М, а отношение
u |
= |
u(M ) − u(M 0 ) |
l |
l |
101

определяет среднюю скорость изменения поля U на участке l .
Определение 7. Если существует предел отношения |
u |
, когда l стремится к нулю, то он |
||||||
|
||||||||
|
|
|
|
|
|
|
l |
|
называется производной поля u(M) в точке M 0 по данному направлению |
||||||||
|
|
0 = {cos α, cos β, cos γ}. |
|
|
||||
l |
|
|
||||||
Этот предел обозначается |
|
|
||||||
|
lim |
u(M ) − u(M 0 ) |
= |
∂u |
. |
|
|
|
|
l |
|
|
|
||||
|
|
l →0 |
|
∂l |
|
|
||
Как практически найти ∂∂ul ?
z N0
l
M0
y
x
Рис. 5
Пусть через точку М0(х0, у0, z0) поля u(M) проведена поверхность равного уровня u(M) = u(M0). Построим вектор нормали к этой поверхности (см. рис. .5) в точке M0
N 0 = ∂∂ux (M 0 )i + ∂∂uy (M 0 )j + ∂∂uz (M 0 )k
l 0 = i cos α + j cos β + k cos γ в точке M0 существует и численно равна скалярному произведению векторов N 0 и l0 :
∂∂ul (M 0 ) = N 0 l0 ,
или в координатной форме
∂∂ul (M 0 ) = ∂∂ux (M 0 )cos α + ∂∂uy (M 0 )cos β + ∂∂uz (M 0 )cos γ.
Доказательство. Согласно определению дифференцируемой функции её полное приращение может быть представлено в виде
|
u(M |
0 |
) = = |
∂u |
(M |
0 |
) |
x + |
∂u |
(M |
0 |
) |
|
y + |
∂u |
(M |
0 |
) z + α( |
x, |
y, |
z) l, |
|||||||||||||||
|
|
|
|
∂z |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
∂x |
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где α — бесконечно малая при |
|
l |
→ 0 , |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
x, |
|
y, |
z — проекции вектора |
|
|
= |
|
|
|
на оси координат: |
|
||||||||||||||||||||||||
|
l |
M 0 M |
|
|||||||||||||||||||||||||||||||||
|
x = |
|
|
l |
cos α , |
|
y = |
l cos β , |
|
|
z = |
|
l cos γ. |
|
|
|
|
|
||||||||||||||||||
|
u |
(M |
0 |
) = |
∂u |
(M |
0 |
)cos α + |
∂u |
(M |
0 |
)cos β + |
∂u |
|
(M |
0 |
)cos γ + α( |
x, |
y, |
z). Прежде чем выполнить |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
l |
|
|
∂x |
|
|
|
∂y |
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
||||||||||||||
предельный переход при l → 0 , заметим, что первые три слагаемые в последнем равенстве не
зависят от |
l и их сумма представляет собой скалярное произведение векторов |
|
|
|
|
||||||||||||||||||||
N |
0 и l0 . |
||||||||||||||||||||||||
Переходим к пределу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
∂u |
(M |
|
) = lim |
u(M 0 ) |
= |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
|
0 |
N |
|
l |
0 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
l |
|
|
|
|
|
|
|
|
|||||||||||||||
|
∂l |
|
l →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Теорема доказана, и формула для вычисления |
∂u |
найдена. |
|||||||||||||||||||||||
∂l |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В плоскопараллельном поле u(M) не зависит от z и |
∂u |
= 0 , поэтому |
|||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
(M ) = |
|
(M )cos α + |
|
|
|
(M )cos β . |
|
|
∂z |
||||||||||||||
|
∂u |
∂u |
∂u |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
∂l |
|
|
∂x |
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 2. Найти производную поля u(M) = х2 − у2 в точке A ( 3, − 4) по направлению l =
3, − 4) по направлению l =  3i − j .
3i − j .
102

Решение. Вычислим направляющие косинусы вектора l :
l = ( 3 )2 + (− 1)2 = 2 , cos α = |
3 |
, |
cos β = − 1 . |
|
2 |
||||
|
|
2 |
Найдём частные производные в указанной точке
∂u |
(A ) = 2x |
|
= 2 3 , |
∂u |
(A ) = − 2y |
|
|
= 8 . |
|
|
|
||||||
|
|
|
|
|
||||
∂x |
A |
|
∂y |
|
A |
|
||
|
|
|
||||||
По формуле (4) вычислим производную по направлению
∂∂ul (A ) = 2 3 23 − 8 21 = −1 .
Здесь отрицательный знак производной поля указывает на то, что в данной точке в направлении данного вектора поле убывает.
3. Градиент скалярного поля
Пусть в поле u(M) дана некоторая эквивалентная поверхность. Возьмём на этой поверхности точку М0 и построим в ней единичный вектор n , направленный по нормали к поверхности в сторону возрастания поля.
Определение 8. Градиентом1 поля u(M) в точке М0 называется вектор, направленный по нормали к эквипотенциальной поверхности, проходящей через точку М0 в сторону возрастания поля и численно равный производной скалярного поля по направлению n .
Обозначение градиента grad u(M 0 ) = ∂∂un n .
Теорема. 1) Вектор grad u(M ) в каждой точке М поля u(M) равен нормальному вектору N , т. е.
grad u(M ) = N = ∂∂ux (M )i + ∂∂uy (M )j + ∂∂uz (M )k . (5)
2) Производная поля в каждой точке М по любому направлению l есть проекция вектора gradu на направление l :
∂u |
(M ) = пр |
|
|
u(M ) . |
(6) |
|||||||
l |
grad |
|||||||||||
|
||||||||||||
∂x |
|
|
|
|
|
|
|
|
|
(5 5 − 3 3 ). |
||
= |
1 |
(4 + 1) |
3 |
|
− (2 + 1) |
3 |
= |
1 |
||||
2 |
|
2 |
||||||||||
|
6 |
|
|
|
|
|
|
6 |
|
|||
Доказательство непосредственно следует из определения градиента и формулы (1) для вычисления производной по направлению, учитывая, что l0 = 1 :
∂u |
(M ) = |
∂u |
(M )cos α + |
∂u |
(M )cos β + ∂u |
(M )cos γ = |
|
|
|
|
|
= |
|||||||||||||
N |
l |
0 |
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
∂l |
|
|
|
∂x |
∂y |
∂z |
|
|
|
|
|
||||||||||||||
= |
|
|
|
|
|
cos( |
|
|
|
) = прl |
|
|
(M ) . |
|
|
|
|
|
|
|
|
||||
|
N |
|
l0 |
N |
, l |
grad |
|
|
|
|
|
|
|
|
|||||||||||
Следствие. Вектор grad u(M ) в каждой точке поля показывает направление, по которому
скорость изменения поля наибольшая из всех скоростей в этой точке и её величина равна модулю gradu(М):
max (∂∂ul )= ∂∂nu = grad u , где n 
 grad u(M ) .
grad u(M ) .
Пример 3. Найти наибольшую скорость изменения поля u = arctg |
|
x |
в точке А(1, 1, 1). |
|
y2 |
+ z2 |
|||
|
|
Решение. Найдём частные производные функции u(x, y, z) и вычислим их в точке А:
103

|
∂u |
= |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
= |
|
|
|
|
y 2 + z2 |
|
|
|
= |
2 |
, |
|
|
|
|
|
|
||||||||||
|
∂x |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
z |
+ y |
|
|
|
|
|
(x + y + z ) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
y 2 + z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− xy |
|
|
|
|
|
|
||||||||||||||||
|
∂u |
|
= |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= − |
1 |
, |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
∂y |
|
|
|
|
x |
2 |
|
|
|
|
|
|
(y |
2 + z2 )3 |
|
|
|
(x 2 + y 2 + z2 ) y 2 + z2 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
y 2 +z2 |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
∂u |
= |
|
|
|
|
|
|
|
|
|
|
|
− xz |
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
∂z |
|
|
(x |
2 |
+ y |
2 |
+ z |
2 |
) |
y |
2 |
+ z |
2 |
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, max ( |
|
|
)= grad u |
|
|
|
|
|
|
|||||||||
|
|
u(A ) = |
|
|
|
2 |
|
|
− |
2 |
|
|
|
− |
|
|
2 |
|
|
∂u |
= |
92 + 181 + 181 = |
1 |
. |
||||||||||||||||||||||||||||||
|
grad |
|
|
|
i |
j |
|
|
|
k |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
6 |
|
|
6 |
∂l |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||
Дифференциальные свойства градиента
1)grad (cu) = c grad u , где c = const ;
2)grad (u1 + u2 ) = grad u1 + grad u2 ;
3) |
|
|
|
(u1 u2 ) = u2 |
|
|
u1 + u1 |
|
u2 ; |
|||||||||||||||||
grad |
grad |
grad |
||||||||||||||||||||||||
|
|
|
|
u |
|
|
|
|
u |
|
|
|
|
u |
|
− u |
|
|
u |
|
|
|
|
|||
4) |
|
|
|
1 |
|
|
2 |
grad |
1 |
1 |
grad |
2 |
|
; |
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
grad |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
u2 |
|
|
|
|
|
|
|
|
|
|
|
u2 |
|
|
|
|
|
|
|
|||
5) |
|
|
f (u) = |
∂f |
|
|
|
u . |
|
|
|
|
|
|
|
|||||||||||
grad |
grad |
|
|
|
|
|
|
|
||||||||||||||||||
|
∂u |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Все эти формулы доказываются, исходя из известных правил дифференцирования и формулы (5).
Рассмотрим обратную задачу. Дан градиент поля, требуется найти само поле, т.е. функцию u(M).
Решение такой задачи существует и определяется с помощью криволинейного интеграла по формуле
u(M ) = ∫ grad u dl + u(M 0 ) ,
M 0 M
где М0М — любая линия, соединяющая точки М0 и М, на которой функция u(M) дифференцируема:
dl = i dx + j dy + k dz .
Формула (7) следует из равенства du = grad u dl . Интегрируя его, получаем
u(M ) − u(M 0 ) = ∫ du = |
∫ |
|
u |
|
. |
grad |
dl |
||||
M 0 |
M 0 M |
||||
Нетрудно заметить, что первая задача (отыскания градиента) аналогична задаче дифференциального исчисления — нахож-дению производной данной функции. Вторая задача аналогична задаче интегрального исчисления — нахождению функции по её производной.
4. Оператор Гамильтона Гамильтон ввёл в употребление символический вектор набла
|
= i |
∂ |
+ j |
∂ |
+ k |
∂ |
, |
|
= {∂ |
, |
∂ |
, |
∂ |
}. |
|
|
|
||||||||||||||
∂x |
∂y |
∂z |
∂y |
∂z |
|||||||||||
|
|
|
|
|
|
∂x |
|
|
|
Этот символ (в дальнейшем будем называть его оператор Гамильтона, или оператор набла) сам по себе не имеет реального смысла, но результат его применения как векторнодифференциального оператора к скалярным или векторным
Теорема. Если функция u(M) дифференцируема в точке M0, то производная поля u(M) по любому направлению
функциям даёт вполне реальную физическую величину в краткой математической записи.
104

Применим оператор Гамильтона к записи градиента и его свойств:
1)grad u = u ;
2)(cu) = c u ;
3)(u1 + u2 ) = u1 + u2 ;
4)(u1 u2 ) = u2 u1 + u1 u2 ;
|
|
|
|
|
|
u |
|
|
|
u |
|
|
|
u |
|
− u |
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5) |
|
|
|
1 |
|
2 |
|
1 |
|
2 |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
u2 |
|
|
|
|
|
|
|
|
|
u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6) f (u) = fu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Докажем некоторые из этих свойств, например: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
• свойство 3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
(u |
|
+ u |
|
) = |
∂(u1 + u2 ) |
|
|
+ |
|
∂(u1 |
+ u2 ) |
|
|
+ |
∂(u1 |
+ u2 ) |
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
1 |
2 |
i |
|
j |
k |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
∂u1 |
|
|
∂u2 |
|
|
|
|
|
∂u1 |
|
|
|
∂u2 |
|
|
|
|
|
∂u1 |
|
|
∂u2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
+ |
|
|
|
i |
+ |
|
|
|
|
|
+ |
|
|
|
|
j |
+ |
|
+ |
|
|
k |
= u |
1 |
+ u |
2 |
; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
∂x |
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
• cвойство 6: по правилу дифференцирования сложной функции имеем
∂f |
= |
∂f |
|
∂u |
, |
∂f |
= |
|
∂f |
|
|
∂u |
, |
|
∂f |
|
|
= |
|
∂f |
|
∂u |
; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
∂x |
|
∂u ∂x |
|
|
∂y |
|
|
|
|
|
∂u |
|
|
|
∂y |
|
∂z |
|
∂u |
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
∂f |
|
|
|
|
∂f |
|
|
|
|
|
|
∂f |
|
|
|
|
|
|
∂f |
|
∂u |
|
|
|
|
|
∂u |
|
|
|
|
∂u |
|
|
|
′ |
|
|
|
|||||
f (u) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u . |
|||||||||||||||||||||
|
∂x |
i |
+ |
∂y |
|
j |
+ |
∂z |
k = |
∂u |
|
|
∂x |
|
i + |
∂y |
|
j + |
∂z |
k |
= fu |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
5. Вихрь и циркуляция векторного поля
Определение 9. Вихрем векторного поля или ротором вектора F = {P, Q, R} (обозначается rot F ) называется вектор, определяемый формулой
|
|
∂R |
|
∂Q |
|
|
∂P |
|
∂R |
|
|
∂Q |
|
∂P |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
rot F = |
|
− |
|
i |
+ ( |
|
− |
|
)j + |
|
− |
|
k , |
|||||||
∂y |
|
∂z |
∂x |
∂x |
|
|||||||||||||||
|
|
|
|
∂z |
|
|
|
|
|
|
∂y |
|||||||||
где P = P(x, y, z), Q = Q(x, y, z), R = R(x, y, z).
Формулу (15.8) можно записать в виде, удобном для запоминания, с помощью оператора Гамильтона как векторное произведение вектора на вектор F :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
k |
|
|
|
|
|
||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
∂ |
|
∂ |
|
∂ |
|
|
|
|
|
||||||
rot F = |
|
= × F . |
||||||||||||||||
∂x |
|
∂y |
|
∂z |
||||||||||||||
|
|
|
P |
|
Q |
R |
|
|
|
|
|
|||||||
Произведения символов ∂∂x , ∂∂y , ∂∂z на функции P, Q, R следует понимать как соответствующие частные производные
∂ |
Q = |
∂Q |
, |
∂ |
R = |
∂R |
, |
∂ |
P = |
∂P |
, . |
∂x |
|
∂x |
∂y |
|
∂y |
∂z |
|
∂z |
|||
Определение 10. Поле вектора F называется потенциальным, если вектор F является градиентом некоторой скалярной функции u(x, y, z), т.е. F = gradu , а сама функция и — потенциалом этого поля.
Необходимым и достаточным условием потенциальности векторного поля F является равенство нулю ротора вектора F :
rot F = 0 , ∂∂Ry − ∂∂Qz = 0 , ∂∂Pz − ∂∂Rx = 0 , ∂∂Qx − ∂∂Py = 0.
Потенциальное поле называется также безвихревым.
Пример 4. Доказать, что поле вектора F {xz 2 , z2 , x 2 z + 2yz} является потенциальным.
105

Решение. Вычислим rot F и убедимся, что он равен нулю в любой точке поля:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
∂ |
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|||||
|
|
rot F = |
|
|
|
= |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
∂x |
|
∂y |
|
|
∂z |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
xz 2 |
|
z2 |
x 2 z + 2yz |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
∂ |
|
(x 2 z + 2yz )− |
∂ |
(z2 ) |
|
|
[∂ |
(x 2 z + 2yz )− |
|
∂ |
(xz 2 )]+ |
||||||||||||||||
|
|
= i |
|
− j |
|||||||||||||||||||||||||||||
|
∂z |
|
|
∂z |
|||||||||||||||||||||||||||||
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+ |
|
|
∂ |
|
(z2 )− |
∂ |
(xz 2 ) = i |
(2z − 2z) − j |
(2xz − 2zx ) − |
|
(0 − 0) = 0, |
||||||||||||||||||||||
k |
|
k |
|||||||||||||||||||||||||||||||
|
|
∂y |
|||||||||||||||||||||||||||||||
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
rot F (M ) = 0, следовательно, векторное поле – потенциальное.
Определение 11. Циркуляцией вектора F {P, Q, R} по замкнутому, ориентированному контуру L называется криволинейный интеграл второго типа
Γ = ∫P(x, y, z)dx +Q(x, y, z)dy + R(x, y, z)dz .
L
Направление обхода контура считается положительным, если обход происходит против часовой стрелки.
Если поле вектора F силовое, то циркуляция есть работа силы F по перемещению материальной точки по замкнутому контуру L.
В потенциальном векторном поле циркуляция по любому гладкому или кусочно-гладкому замкнутому контуру равняется нулю.
Укажем более компактную запись формулы Введём векторный символ дифференциала дуги
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dl |
|
|
|
|
dl = i |
dx + j |
dy + k dz , |
|||||
|
|
= τ |
|
||||||||||
где τ |
|
— единичный касательный вектор ориентированного замкнутого контура L, |
|||||||||||
dl = |
dx 2 |
+ dy 2 + dz2 — дифференциал дуги. |
|||||||||||
Тогда формула (15.11) примет вид |
|||||||||||||
|
ΓL |
= ∫ Pdx +Qdy + Rdz = ∫ F dl . |
|||||||||||
|
|
|
|
L |
|
|
|
|
|
|
L |
||
Используя свойства скалярного произведения, получим ещё одну формулу |
|||||||||||||
|
ΓL = ∫(F τ )dl = ∫(прτ |
F )dl . |
|||||||||||
|
|
|
|
L |
|
|
L |
||||||
Пример 5. Вычислить циркуляцию векторного поля F {− z − 3x 2 , y − 2z, 2y − z} вдоль линии
пересечения плоскости (р) х + у + 2z = 4 с координатными плоскостями, направление положительное.
z
2 |
C |
|
4 |
o |
B y |
4 A x
Рис. 6
Решение. Составляем криволинейный интеграл по заданному контуру и разбиваем его на сумму трёх интегралов по отрезкам, составляющим этот контур (см. рис. 6):
Γ = ∫ F dl = ∫ F dl + ∫ F dl + ∫ F dl ,
AB BC CA
где F dl = (− z − 3x 2 )dx + (y − 2z)dy + (2y − z)dz,
AB: z = 0, x = t, y = 4 – t; dz = 0, dx = dt, dy = – dt, tA = 4, tB = 0; BC: x = 0, z = t, y = 4 – 2t; dx = 0, dz = dt, dy = – 2dt, tB = 0, tC = 2; CA: y = 0, z = t, x = 4 – 2t; dy = 0, dz = dt, dx = – 2dt, zC = 2, zA = 0.
Вычисляем циркуляцию, сводя криволинейные интегралы в определённые, по выбранному параметру:
106
|
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
|
|
t 3 |
|
|
|
t 2 |
4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∫ F |
dl |
= ∫ |
[(− |
3t |
|
)dt + (4 − t )(− dt )] = 3 |
|
|
|
+ 4t |
− |
|
|
= 64 + 16 − 8 =72, |
|||||||||||||
|
3 |
|
2 |
|||||||||||||||||||||||||
|
AB |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
[(4 − 2t |
− 2t )(− 2dt ) + (8 − 4t |
− t )dt ] |
|
2 |
|
|
t 2 |
|
|
2 |
|
||||||||
|
∫ |
|
|
|
dl |
= ∫ |
= 3∫ tdt =3 |
|
|
= 6, |
||||||||||||||||||
F |
||||||||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||
|
BC |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
0 |
(− t − 3(4 − 2t )2 )(− 2dt ) − tdt |
|
|
0 |
|
0 |
(4 − 2t )2 d(4 − 2t ) = |
|||||||||||||
|
∫ |
|
|
dl |
= ∫ |
= ∫ tdt |
− 3∫ |
|||||||||||||||||||||
F |
||||||||||||||||||||||||||||
|
CA |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||||
2 |
− (4 − 2t )3 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
t |
|
|
= −2 |
− 64 = −66. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда Г = 72 + 6 – 66 = 12.
Ответ: 12.
6. Поток векторного поля
Определение 12. Потоком вектора F {P, Q, R} через ориентированную поверхность σ называется поверхностный интеграл второго типа
Π = ∫∫ P(x, y, z)dydz +Q(x, y, z)dxdz + R(x, y, z)dxdy .
σ
Выведем эту формулу, исходя из физического смысла введённого понятия. Рассмотрим частный случай стационарного поля, когда скорость течения жидкости во всех точках поля одна и та же v = const (см. рис. 15.7). Количество жидкости Q, протекшее за единицу времени через прямоугольник A ′B′C′D′ со скоростью v , равно произведению его площади S1 = SA ′B′C′D ′
на скорость v :
Q = S1 v .
Величина Q постоянна в любом сечении, параллельном данному.
Очевидно, что это же количество жидкости протечёт и через площадку ABCD, составляющую угол ϕ с прямоугольником A’B’C’D’. Тогда
S1 = S cosϕ ,
где S — площадь ABCD,
Q = S cos ϕ v = S vn ,
где vn — проекция скорости на нормаль n .
Разумеется, формула будет верна для площадки любого вида, например, как на рис. 15.8.
C′ |
C |
n |
|
n |
|
|
ϕ |
||
B′ |
B |
ϕ v |
v |
|
D′ |
|
D |
|
|
A′ |
A |
|
Рис..8 |
|
|
Рис. 7 |
|
|
Перейдём к общему случаю. Решим задачу о вычислении количества жидкости, протекшего через произвольную поверхность σ. Пусть в некоторой части пространства задано поле скоростей жидкости, т.е. в каждой точке M(x, y, z) этого пространства задан переменный вектор скорости
v (M ) = P(M )i + Q(M )j + R(M )k .
107
z |
ni |
vi
Mi σi
σ
y
x
Рис. 9
Возьмём гладкую ориентированную поверхность σ (рис..9) и подсчитаем количество жидкости, протекающее через эту поверхность. Разобьём поверхность σ сетью произвольных кривых на п участков σi, в каждом из которых выберем произвольную точку Mi. Будем считать, что каждая площадка σi, в силу её малости, плоская и поток, проходящий через неё, – постоянный, именно такой, как в точке Mi в направлении нормали ni, построенной в точке Mi.
Можно приближённо подсчитать количество жидкости, протекшее через поверхность σ по формуле суммируя результаты по всем i = 1, 2, …, n :
n
Q ≈ ∑ σ i vi cos ϕi ,
i = 1
где Δσi — площадь участка σi,
vi = P(M i )i + Q(M i )j + R(M i )k — скорость поля в точке Mi,
ϕi — угол между нормалью к поверхности σi, построенной в точке Mi, и вектором скорости
vi .
Преобразуем формулу (16), используя свойства скалярного произведения вектора v на единичный вектор нормали
n = i cos α + j cos β + k cos γ , n = 1 ,
n |
|
|
n |
|
Q ≈ ∑ |
( |
vi , |
ni ) σi Q ≈ ∑ |
(Pi cos α i + Qi cos βi + Ri cos γ i ) σ i . |
i =1 |
|
|
i = 1 |
|
Перейдём к пределу при n → ∞, когда maxdi → 0, т. е. каждая площадка σi стягивается в точку:
n
Q = lim ∑ (Pi cos α i + Qi cos βi + Ri cos γ i ) σ i .
n → ∞ i = 1
Величина Q называется потоком жидкости через поверхность σ и выражается поверхностным интегралом
Q = ∫∫ (P(x, y, z) cos α +Q(x, y, z) cos β + R(x, y, z) cos γ)dσ =
σ
= ∫∫ Pdxdy |
+ Qdxdz + Rdxdy |
|
= Π |
|
|
|
|
|
|
||||||||||
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ |
|
|
|
|
∫∫ |
|
|
|
|
|
|
|
∫∫ |
|
|
|
|
или |
Π = |
v n dσ = |
v |
|
|
|
|
|
|
(пр |
n |
v )dσ . |
|||||||
|
|
cos v, n |
dσ = |
|
|
||||||||||||||
|
|
σ |
|
|
|
|
σ |
|
|
|
|
σ |
|
|
|
|
|||
Таким образом, мы получили различные формулы для вычисления потока векторного поля с помощью поверхностных интегралов первого и второго типов.
Пример 6. Вычислить поток вектора a = x1 i + y1 j + 1z k через полную поверхность эллипсоида xa22 + yb22 + zc22 = 1 в сторону внешней нормали.
Решение. Подынтегральная функция терпит разрыв в точке (0, 0, 0) – центре эллипсоида. Формулу Остроградского нельзя применять, хотя поверхность и замкнута, но можно
108
воспользоваться формулой (15.17), связывающей поверхностные интегралы первого и второго типов:
|
∫∫ |
x |
|
y |
|
z |
|
∫∫ |
x |
|
y |
|
z |
|
Π = |
|
dzdy |
+ |
dxdz |
+ |
dxdy |
= |
cosα |
+ |
cosβ |
+ |
cos γ |
||
|
|
|
|
|
|
|
|
dσ. |
||||||
|
σ |
|
|
|
|
|
|
σ |
|
|
|
|
|
|
Если поверхность задана уравнением F(x, y, z) = 0, то
|
|
∂F |
|
∂F |
|
∂F |
||
|
|
|
|
|||||
N = |
|
, |
|
, |
|
. |
||
∂x |
∂y |
|
||||||
|
|
|
|
|
∂z |
|||
Представим уравнение эллипсоида в виде
F (x, y, z) = |
x 2 |
+ |
x 2 |
+ |
x 2 |
− 1 = 0 |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
и найдём частные производные функции F(x, y, z)
∂F |
= |
2x |
, |
∂F |
= |
2x |
, |
∂F |
= |
2x |
, |
N = 2 |
x2 |
+ y2 |
+ |
z2 . |
|
∂x |
a2 |
∂y |
b2 |
∂z |
c2 |
a4 |
|||||||||||
|
|
|
|
|
|
|
b4 |
|
c4 |
Вычислим направляющие косинусы нормали (см. п. 14.4)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
cos α = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
a |
2 |
|
|
|
|
|
x 2 |
|
|
|
|
|
y2 |
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
(∂F )2 |
|
|
+ ∂F |
+ (∂F )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a4 |
|
|
b4 |
c4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
cos β = |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
, cos γ = |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
b2 |
|
|
|
x 2 |
+ |
y2 |
+ |
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
+ |
|
y 2 |
|
+ |
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a4 |
b4 |
|
|
|
c4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a4 |
|
|
b4 |
|
|
c4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
подставим их в исходную формулу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Π = |
|
2 |
+ |
|
2 |
|
|
+ |
|
|
|
2 |
|
∫∫ 2 |
|
2 |
|
|
|
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
dσ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
a |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
c |
|
|
|
σ |
|
|
|
x |
4 + |
y |
4 |
|
+ |
|
z |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
b |
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы перейти к двойному интегралу, необходимо выбрать координатную плоскость, на |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
которую будем проектировать поверхность, пусть это будет xoy, тогда dσ = |
dxdy и |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos γ |
|
|
|
|
|
|
соответственно |
|
|
+ c2 |
∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= a2 |
|
+ b2 + c2 |
∫∫ |
|
|
z . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Π = a |
2 |
+ b2 |
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
y2 |
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
cos γ |
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
4 |
|
b |
4 |
c |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
σ : z = +c 1 − |
|
x2 |
|
− |
|
y2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
с нормалью |
|
|
|
|
образующей острый угол с осью oz, cos γ ≥ 0; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
N1, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
σ2 : z = −c 1 − |
x |
2 |
− |
y |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
a |
2 |
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
с нормалью |
|
|
2, |
|
образующей тупой угол с осью oz, cosγ ≤ 0. Таким образом, приходится |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
N |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
рассматривать сумму потоков: П1 – через σ1 , П2 – через σ2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫∫ |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Π = Π 1 + Π 2 = |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ1 |
|
|
|
σ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= c |
|
a2 |
+ b2 + c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
− ∫∫ |
|
|
|
|
|
2 |
|
2 |
|
|
= = 2c a2 |
+ b2 + c2 |
∫∫ |
|
|
2 |
|
2 . |
||||||||||||||||||||||||||||||||||||
|
|
+ ∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
dxdy |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dxy + c 1 − |
x |
|
− |
y |
|
|
|
|
|
Dxy − c 1 − |
x |
− |
y |
|
|
|
|
|
|
|
|
|
|
|
|
Dxy |
1 − |
x |
|
− y |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
b |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||
109
Вычислим двойной интеграл в обобщённых полярных координатах:
x = aρ cos ϕ, y = bρ sin ϕ, I = abρ;
уравнение эллипса |
|
x2 |
+ |
y2 |
= 1 принимает вид ρ2 = 1; |
|||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
2π |
|
|
|
1 |
|
abρdρ |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Π = 2c |
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
|
dϕ |
|
|
|
|
|
|
= |
|
|
|
||||||
|
|
|
|
b2 |
c2 |
∫ |
∫ |
|
|
2 |
|
|
|
|||||||||||||||||||
|
a2 |
|
|
|
|
|
|
|
|
1 |
− ρ |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= abc |
1 |
|
+ |
|
1 |
+ |
|
1 |
|
|
2π |
− (1 − ρ2 )12 |
1 |
= |
4π |
(b2 c2 + a2 c2 + a2b2 ). |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
abc |
|||||||||
a2 |
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
7. Дивергенция. Соленоидальное поле
Прежде чем перейти к понятию дивергенции, разберёмся, почему величина потока принимает положительное или отрицательное значение.
Пусть, например, по трубе течёт газ под давлением P1 и внутрь трубы помещён шар с тем же газом под давлением P2 > P1. Окружим шар некоторой проницаемой поверхностью σ, и в шаре сделаем отверстие. Тогда часть газа из шара будет выходить в основной поток, а из объёма, ограниченного поверхностью σ, будет выходить газа больше, чем в него входить. Отверстие в шаре в этом случае будет источником и поток через поверхность σ будет положителен. Если же наоборот: давление внутри шара P2 < P1, тогда часть газа из основного потока через отверстие будет входить в шар. В этом случае отверстие в шаре является стоком и поток газа через поверхность σ будет отрицательным.
Вернёмся к формуле Остроградского. Стоящее под знаком тройного интеграла выражение называется дивергенцией (или расходимостью) вектора
F= P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k
иобозначается символом
div F = ∂P + ∂Q + ∂R
∂x ∂y ∂z
или (с помощью оператора Гамильтона) дивергенция равна скалярному произведению векторов и F :
div F = F .
Формула Остроградского перепишется в виде
∫∫Fndσ = ∫∫∫div F dxdydz ,
σT
если вектор F — скорость течения жидкости, то формула обозначает поток поля F . Если П > 0, то говорят, что в объёме V, ограниченном поверхностью σ, имеются источники поля, если П < 0, то в объёме V имеются стоки.
Установим численную характеристику плотности источников и стоков поля в любой его точке, т.е. дадим точное определение дивергенции. Зафиксируем в векторном поле F произвольную точку М. Окружим её некоторой замкнутой гладкой поверхностью σ (например, сферой с центром в точке М). Вычислим поток поля через σ:
Π = ∫∫ F d σ.
σ
Пусть V означает объём, ограниченный σ, тогда отношение
∫∫ F dσ
Π = σ
V V
110
определяет среднюю плотность источников (П > 0) или стоков (если П < 0), распределённых в объёме V.
Определение 13. Предел отношения VΠ , когда поверхность σ стягивается в точку М, называют дивергенцией или расходимостью векторного поля в точке М.
Дивергенция обозначается
∫∫ F dσ
div |
|
(M ) = lim |
σ |
, |
F |
||||
|
|
d(σ) → 0 |
V |
|
где d(σ) — диаметр поверхности σ. Замечание
•в этом определении предполагается, что предел существует независимо от того, как поверхность σ стягивается в точку;
•если divF(M) > 0, то в точке М имеется источник;
•если divF(M) < 0, то в точке М имеется сток;
•дивергенция и есть плотность источников;
•если divF(M) = 0, то поле называется соленоидальным (или трубчатым), т.е. в этом поле отсутствуют источники и стоки, расход жидкости через любое сечение векторной трубки имеет одно и то же значение.
Пример 7. Вычислить дивергенцию поля радиус-вектора
r = xi + yj + zk .
Решение. Ищем соответствующие частные производные от каждой координаты вектора
r |
x |
= x, r |
y |
= y, |
|
r |
z |
= z, |
|
∂rx |
= 1, |
∂ry |
= 1, |
∂rz |
= 1, |
||||||
|
|
∂x |
∂y |
∂z |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
div |
|
(M ) = |
∂rx |
|
+ |
|
∂ry |
+ |
∂rz |
= 3. |
|
|
|
|
|||||||
r |
|
|
|
|
|||||||||||||||||
∂x |
|
|
∂y |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
||||||
В каждой точке поля имеется источник плотности, равный 3 ед.
Пример 8. Найти поток электростатического поля точечного заряда q, помещённого в точке М через поверхность сферы радиуса R с центром в точке М.
Решение. Поле точечного заряда, как известно, задаётся вектором напряжённости
E = rq3 r ,
где r — радиус-вектор, проведённый из точки, в которую помещён заряд. Выберем систему координат, начало которой поместим в центре сферы (см. рис. 15.10). Тогда
r = r = x 2 + y 2 + z2 .
Найдём div E :
|
|
|
|
|
|
|
|
|
|
|
|
− |
3 |
|
|
|
|
|
|
|
|
− |
3 |
|
|
|
|
|
− |
3 |
|
|
|
||
|
E = q (x 2 |
+ y 2 |
+ z2 ) |
2 xi + |
(x 2 + y 2 + z2 ) |
|
2 yj + (x 2 |
+ y 2 |
+ z2 ) |
2 zk , |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
− |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
− |
5 |
|
|
|
|
|
|
|
||
Ex |
= q (x2 |
+ y |
2 |
+ z2 ) |
2 − 3 2x2 (x2 + y2 |
+ z2 ) |
2 = q(r |
−3 − 3x2r −5 ), |
|||||||||||||||||||||||||||
∂x |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
E |
y |
= q(r −3 |
− 3y2r −5 ), |
|
|
|
∂ |
|
E |
z |
= q(r −3 |
− 3z2r −5 ). |
|
|
|
|
|
|
||||||||||||||
|
|
∂y |
|
|
∂z |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Складывая производные, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
div |
|
= q[3r −3 |
− 3r −5 (x2 |
+ y2 |
+ z2 )]= q(3r −3 |
− 3r −3 )= 0. |
|
|
|
|
|
|||||||||||||||||||||||
|
E |
|
|
|
|
|
|||||||||||||||||||||||||||||
Таким образом, в любой точке поля, где определён вектор напряжённости E , нет ни источников, ни стоков. Но в самой точке, где помещён заряд, r = 0, вектор E не определён и для вычисления потока мы не можем воспользоваться формулой Остроградского.
111
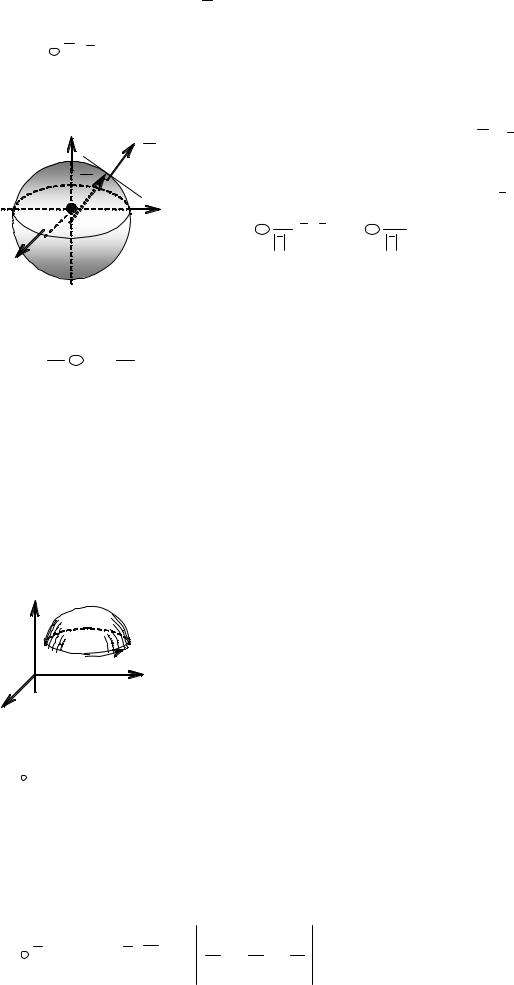
Вычисляем поток вектора E непосредственно, с помощью поверхностного интеграла первого типа
Π = ∫∫ E n dσ,
σ
где σ — внешняя поверхность сферы.
z |
В нашем случае (см. рис. 10) вектор N = r (по определению: |
||
N |
нормалью называется вектор, проведённый в точке касания |
||
r |
перпендикулярно касательной). |
||
y |
Обозначим единичный вектор нормали r0 . Тогда |
||
M |
Π = |
∫∫ r 3 |
∫∫ r 2 |
|
|||
x |
q (r r0 )dσ = |
qdσ . |
|
|
σ |
σ |
|
|
|
||
Рис..10
Π = Rq2 ∫∫dσ = Rq2
σ
Так как заряд находится в центре сферы, то длина радиусавектора любой точки сферы будет равна радиусу сферы R, и тогда имеем
4πR2 = 4πq.
Как видим, поток точечного заряда не зависит от радиуса сферы.
Вывод: через любую сферу с центром в точечном заряде проходит одно и то же число векторных линий.
8. Теорема Стокса.
Связь поверхностных интегралов с криволинейными
Пусть поверхность σ ограничена замкнутой кривой L (см. рис. 11). И поверхность, и контур
предполагаем гладкими или кусочно-гладкими. Ориентируем поверхность σ так, чтобы обход |
||
z |
контура происходил против часовой стрелки, т. е. в положительном |
|
направлении (см. п. 14.2). |
||
σ |
||
L
y
x
Рис. 11
Пусть функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны на поверхности σ вместе со своими частными производными первого порядка.
При этих условиях имеет место формула Стокса, устанавливающая связь между криволинейным интегралом по замкнутому контуру L и интегралом по поверхности σ, ограниченной этим контуром (или, говорят, натянутой на контур),
∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz =
L
|
|
∂R |
|
∂Q |
|
∂P ∂R |
|
|
|
∂Q |
|
|
∂P |
|
|
|
|||||||||||
= |
∫∫ |
|
− |
|
|
|
|
− |
|
|
|
|
|
|
− |
|
|
|
|
= |
|
|
|||||
∂y |
∂z |
|
∂z |
∂x |
|
|
∂x |
∂y |
|
|
|||||||||||||||||
|
|
|
|
|
dzdy + ( |
|
|
|
)dzdx + |
|
|
|
|
|
|
dxdy |
|
|
|||||||||
|
σ |
|
∂y |
|
∂z |
|
∂z |
|
|
∂x |
|
|
|
∂x |
|
|
|
∂y |
|
|
|
||||||
|
∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
∂R |
|
∂Q |
|
∂P |
|
|
∂R |
|
|
|
∂Q |
|
|
|
∂P |
|
|
|
|||||||
= |
|
|
|
|
− |
|
|
cos α + ( |
|
|
− |
|
)cosβ + |
|
|
|
− |
|
cos γ |
|
dσ. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведём краткую запись этой формулы: |
|
|
|
|
|
||||||||||||||||||||||
∫ F dl |
|
= ∫∫rot F dσ = ∫∫ |
cos α |
cos β |
cos γ |
dσ. |
|
|
|
||||||||||||||||||
|
|
∂x |
|
∂y |
|
|
|
∂z |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
∂ |
|
|
|
∂ |
|
|
|
|
|
|
|
|
L |
|
|
|
|
σ |
|
|
|
|
σ |
|
|
P |
|
Q |
|
|
|
R |
|
|
|
|
|
|
|
|
112
Механический смысл формулы Стокса: циркуляция вектора F по замкнутому контуру L равна потоку ротора вектора F через произвольную поверхность σ, ограниченную этим контуром.
Доказательство формулы проведём для простейшего случая, когда прямые, параллельные координатным осям, пересекают гладкую поверхность σ не более чем в одной точке (см. рис. z n 12). Пусть поверхность σ однозначно проектируется в область D
σплоскости хоу, а контур L, ограничивающий поверхность,
M L
y
D
x |
l |
M1
Рис. 12
проектируется соответственно в l – границу области D.
Рассмотрим одно из слагаемых формулы и докажем, например, равенство
∫ P(x, y, z)dx = ∫∫ ∂∂Pz dzdx − ∂∂Py dxdy ,
L σ
где σ — поверхность, заданная уравнением z = f (x, y), L – граница этой поверхности (замкнутый контур ориентирован положительно).
Заменяя в левой части формулы (24) переменную z (поскольку контур L принадлежит поверхности), получаем криволинейный интеграл вида
∫ P(x, y, z) dx = ∫ P[x, y, f (x, y)]dx = ∫ ϕ(x, y)dx,
L |
L |
l |
где ϕ(x, y) = P[x, y, f (x, y)],
l – проекция контура L на плоскость хоу.
Формула (25) справедлива, поскольку точки M(x, y, z) L и M1(x, y, 0) l имеют равные координаты х, у (см. рис. 13). Применяя формулу Грина получаем
∫ ϕ(x, y)dx = −∫∫ ∂∂yϕ dxdy .
L D
Переписываем формулу
∫ P(x, y, z)dx = −∫∫ ∂∂yϕ dxdy .
L D
Используем правило дифференцирования сложной функции
∂ϕ |
= |
∂ |
P[x, y, f (x, y)] = |
∂P |
+ |
∂P |
|
∂f (x,y ) |
= |
∂P |
+ |
∂P |
|
∂z |
. |
∂y |
∂y |
∂y |
∂f (x,y) |
∂y |
∂y |
|
|
||||||||
|
|
|
|
|
|
∂z ∂y |
|||||||||
Подставляя последнее равенство в (15.26) и возвращаясь от двойного интеграла к поверхностному (см. п. 14.1), получаем
∫ |
|
|
|
∂P ∂P ∂z |
|
|
∂P |
||
Pdx |
= − |
∫∫ |
∂y |
+ |
∂z ∂y |
= − |
∫∫ |
∂y |
|
|
|
|
dxdy |
|
|
||||
L Dxy σ
|
|
|
∂P ∂z |
|
∂P |
|
||
|
∫∫ |
|
|
|
|
|
|
|
|
|
∂z |
∂y |
|
∂y |
|||
= |
|
− |
|
|
|
cos γ − |
|
cos γ dσ. |
|
σ |
|
|
|
|
|
|
|
+ |
∂P ∂z |
|
∂z |
cos γdσ = |
|
|
∂y |
|
Теперь заметим, что в нашей задаче поверхность σ задана уравнением z = f(x, y), запишем его в общем виде F(x, y, z) = 0, а именно: F(x, y, z) = f(x, y) – z.
Найдём вектор нормали N = ∂∂xf i + ∂∂yf j − k . Oн коллинеарен единичному вектору
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
n |
= i |
cos α + j |
|
cos β + k cos γ, поэтому их проекции пропорциональны: |
||||||||||
|
|
|
|
|
|
∂f |
|
−1 |
|
|
|
||||
|
|
|
|
|
|
∂y |
= |
. |
|
|
|||||
|
|
|
|
|
|
|
cos |
γ |
|
|
|||||
|
|
|
cos β |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
113 |
||
Получаем ∂∂yz cos γ = − cos β.
Подставляем последнее равенство в окончательно имеем
∫ |
|
|
|
∂P |
|
∂P |
|
∂P |
|
|
∂P |
|
P(x, y, z)dx |
= |
∫∫ |
∂z |
cos β − |
∂y |
|
∫∫ ∂z |
dxdz |
− |
∂y |
dxdy . |
|
|
|
|
|
cos γ dσ = |
|
|
||||||
L |
|
|
σ |
|
|
|
|
σ |
|
|
|
|
Аналогичным образом доказываются и следующие формулы:
|
|
∂Q |
cos γ − |
∫ Qdy = ∫∫ |
∂x |
||
L |
σ |
|
|
|
|
∂R |
cos α − |
∫ Rdz = ∫∫ |
∂y |
||
L |
σ |
|
|
∂Q |
|
∂Q |
|
∂Q |
|
∂z |
|
∫∫ ∂x |
dxdy − |
∂z |
dydz , |
|
cos α dσ = |
|
|
||
|
|
σ |
|
|
|
∂R |
|
∂R |
|
∂R |
|
∂x |
|
∫∫ ∂y |
dydz − |
∂x |
dxdz . |
|
cos β dσ = |
|
|
||
|
|
σ |
|
|
|
Складывая три равенства, получим формулу Стокса (в координатной форме)
∫ Pdx + Qdy + Rdz =
L
|
|
∂R ∂Q |
|
∂P ∂R |
|
∂Q ∂P |
|
|||||||||
= ∫∫ |
|
− |
|
cos α + |
|
− |
|
cos |
β + |
|
− |
|
cos γ dσ. |
|||
∂y |
∂z |
∂z |
∂x |
∂x |
∂y |
|||||||||||
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, формула доказана. |
|
|
|
|
|
|
||||||||||
Перепишем её в векторной форме |
|
|
|
|
|
|
||||||||||
∫ F dl |
= ∫∫ rot F dσ. |
|
|
|
|
|
|
|
|
|
|
|
||||
L |
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
||
Последнее равенство обычно называют формулой Стокса.
Заметим, что мы доказали теорему Стокса для простейшего случая, когда прямые, параллельные координатным осям, пересекают поверхность не более чем в одной точке. Но теорема справедлива и в более сложных ситуациях, когда поверхность требуется разбить на части, которые будем называть правильными, или простейшими, т. е. отвечающими условиям теоремы. Соответственно границей каждого такого участка выбираем замкнутый контур, ориентированный в положительном направлении (сравните с применением формулы Грина).
Пример 10. Найти с помощью формулы Стокса циркуляцию векторного поля
a = {2yz, x 2 + 2y, xy } вдоль контура треугольника, образованного пересечением плоскости
(р) х + 3у + 2z − 6 = 0
с координатными плоскостями в положительном направлении (рис. 13). Решение. Находим вихрь вектора a
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3 C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
rot a |
= |
∂ |
|
|
|
∂ |
|
|
|
|
∂ |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
∂x |
|
|
∂y |
|
|
|
∂z |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 y |
|
|
|
|
|
|
2yz |
x 2 + 2y |
xy |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
B |
|
Раскладываем определитель по элементам первой строки |
|||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||
6 A |
|
|
|
rot a |
= i ∂ |
(xy ) − ∂ |
|
(x 2 |
+ 2y ) − − j ∂ |
(xy ) − ∂ |
(2yz ) + |
|||||||||||||||||||||||
x |
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
∂x |
|
∂z |
|
||||||
Рис.13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
+ |
|
|
∂ |
(x 2 + 2y )− |
|
∂ |
(2yz ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
k |
|
= i |
(x − 0) − j (y − 2y) + |
k |
(2x − 2z). |
|||||||||||||||||||||||||||
|
|
|
∂y |
|||||||||||||||||||||||||||||||
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выбираем любую поверхность, натянутую на контур треугольника АВС. Пусть это будет плоскость р (см. рис. 14), её уравнение задано. Согласно правилу ориентации нормаль к ней
N {1, 3, 2} направлена вверх, т. е. образует острые углы с каждой из координатных осей.
114
z
3 C N
|
|
2 |
y |
|
|
Составляем формулу Стокса |
|
|||||
|
|
|
|
Γ = ∫2yzdx |
+ (x |
2 |
+ 2y )dy |
|
|
|||
|
|
B |
|
|
|
+ xydz |
= |
|||||
|
|
|
|
|
|
|
||||||
6 A |
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
= ∫∫ xdydz |
|
|
|
|
|
||
x |
Рис. 14 |
|
|
|
+ ydxdz + (2x − 2z)dxdy = |
|||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
= ∫∫ (x cos α + y cos β + (2x − 2z) cos γ)dσ. |
||||||
|
|
|
|
|
|
|
σ |
|
|
|
|
|
Находим направляющие косинусы |
|
|
|
|
||||||||
n = |
N , N = 12 + 32 + 22 = 14, |
|
|
|
|
|
||||||
|
N |
|
|
|
|
|
|
|
|
|
|
|
cos α = |
1 |
, |
cos β = |
3 , |
cos γ = |
2 |
|
|
|
|
||
|
|
14 |
|
|
|
14 |
|
14 |
|
|
|
|
и подставляем их в последний интеграл |
|
|
||||||||||
|
|
x |
|
3y |
|
4x − 4z |
|
|
|
|
|
|
Γ = |
∫∫ |
14 |
+ |
14 |
+ |
14 |
|
|
|
|
|
|
|
|
|
|
dσ. |
|
|
|
|
|
|||
σ
Вычисляем интеграл, переведя его в двойной, например по области Dxz (см. рис. 15), спроектировав р на плоскость xoz.
z |
|
|
|
|
Тогда dσ = |
dxdz |
= |
|
14 dxdz |
, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3 |
C |
|
|
cosβ |
|
|
3 |
|
|
|
|
|
|
|
|||||||||||
|
|
а в подынтегральной функции переменную у заменим, |
|||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
используя уравнение σ, т. е плоскости p, y = |
6 − x − 2z |
. |
|||||||||||||||||
|
|
|
|
|
6 x |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
Получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Рис. 15.15 |
Γ = + ∫∫ |
1 |
|
x |
+ 3 |
6 |
− x − 2z |
|
+ 4x − 4z |
|
14 dxdz |
= |
|
|||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
||||||||||
|
|
|
|
|
|
Dxz |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
6 − 2z |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 31 ∫ dz |
∫ |
(6 − 6z + 4x )dx = 31 |
∫ dz[6(1 − z)x + 2x 2 ]20(3 − z) = |
|
|
|
|
|
|
|
|
|
|
||||||||||||
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
4 |
∫3 [3(3 + z2 − 4z)+ 2(3 − z)2 ]dz = 4 3z + |
z3 |
|
− 2z2 − 92 (3 − z)3 |
3 |
= 24. |
|
|
|
|
|
|||||||||||||
3 |
3 |
|
|
|
|
|
|||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
115
