2. Алгоритм симплекс-метода:

1. Заполняем исходную таблицу (считается, что исходный базис найден).

2. Ищем в нижней строке максимальный положительный элемент (кроме 0). Если таких нет, то задача решена. Пусть _j - максимальное положительное число в нижней строчке.

3. В j-том столбце ищем положительные коэффициенты а_kj (если таких нет, то задача не имеет решения). Во вспомогательный столбец заносим b_k/а_kj. Пусть минимальный элемент во вспомогательном столбце находится в i-й строке. На пересечении разрешающего столбца (j) и разрешающей строки (i) находится разрешающий элемент a_ij.

4. Заполняем новую таблицу в следующем порядке:

1. заголовок;

2. первый столбец (вместо х_i пишем х_j);

3. единичные столбцы;

4. разрешающую строку (делим на а_ij);

5. остальные строчки по порядку.

5. Возвращаемся к пункту 2.

ОСНОВНАЯ ФОРМУЛА симплекс-преобразования: (пункт 4e) имеет вид:

3. Пример.

Решим с помощью симплекс-метода задачу:

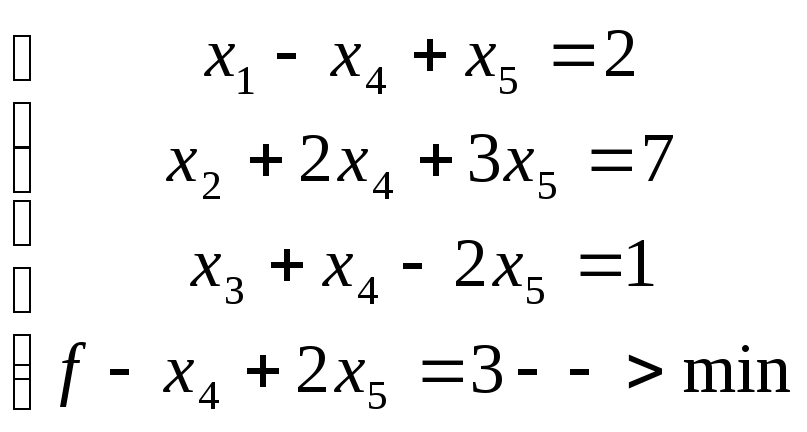
Видно, что данная система решена относительно свободных переменных х4 и х5 и свободных при базисных переменных х1, х2 и х3. Заполняем исходную симплекс-таблицу и действуем далее по алгоритму.

Базис	Свободные члены	х1	х2	х3	х4	х5	Вспомогательный столбец
х1	2	1	0	0	-1	1	2 <- минимум
х2	7	0	1	0	2	3	7/3
х3	1	0	0	1	1	-2
f	3	0	0	0	-1	2

Базисное решение (2,7,1,0,0) f=3

Базис	Свободные члены	х1	х2	х3	х4	х5	Вспомогательный столбец
х5	2	1	0	0	-1	1
х2	1	-3	1	0	5	0	0.2 <- минимум
х3	5	2	0	1	-1	0
f	-1	-2	0	0	1	0

Базисное решение (0,1,5,0,2) f= -1

Базис	Свободные члены	х1	х2	х3	х4	х5	Вспомогательный столбец
х5	2.2	0.4	0.2	0	0	1
х4	0.2	-0.6	0.2	0	1	0
х3	5.2	1.4	0.2	1	0	0
f	-1.2	-1.4	-0.2	0	0	0

Базисное решение (0,0,5.2,0.2,2.2) f= -1.2

Видим, что данная таблица является последней и соответствующее ей базисное решение является оптимальным. Ответ получаем такой: fmin =-1.2, вектор X=(0;0;5.2;0.2;2.2).

1. Содержание лабораторной работы.

1. Ответить на вопросы контролирующей программы.

2. Решить. предложенный вариант задачи графическим способом

3. Решить предложенный вариант задачи симплекс-методом, используя графическое решение для контроля правильности вычислений.

4. Составить, отладить и протестировать на контрольных примерах программу решения задачи линейного программирования симплекс-методом.

5. Составить отчет, содержащий цель и назначение работы, постановку задачи и текст программы.

13. Элементы математической статистики

Процесс познания окружающего нас мира включает наблюдение и эксперимент. Результаты наблюдений во многих случаях можно представить последовательностью действительных чисел .

Для того, чтобы из ряда наблюдений можно было извлечь полезную информацию, необходимо иметь модель явления. Вероятностные модели оказываются наиболее пригодными при анализе явлений, исходы которых обладают некоторой степенью неопределенности. Понятие неопределенности в теории вероятностей формализуется путем введения распределения вероятностей на множестве . В простейшем случае, когда конечное или счетное множество, задаются вероятности всех его элементов , так что и .

Любое множество называют в этом случае событием, а его вероятность определяют формулой .

Взаимоотношение явления и его вероятностной модели имеет статистический характер, то есть обнаруживается при повторных наблюдениях за явлением. Частоты исходов в длинном ряду испытаний стабилизируются, их колебания с ростом числа испытаний уменьшаются. Это эмпирический факт, называемый законом устойчивости частот, наблюдается в самых различных ситуациях. Уже выходя за пределы реального опыта, полагают, что при неограниченном повторении частоты стремятся к пределам, которые и принимают за вероятности соответствующих исходов или событий.