
Лаба№2 / Лаба2-Полиномиальная аппроксимация
.docПолиномиальная аппроксимация.
По заданной таблице значений функции составить формулу интерполяционного многочлена Лагранжа.
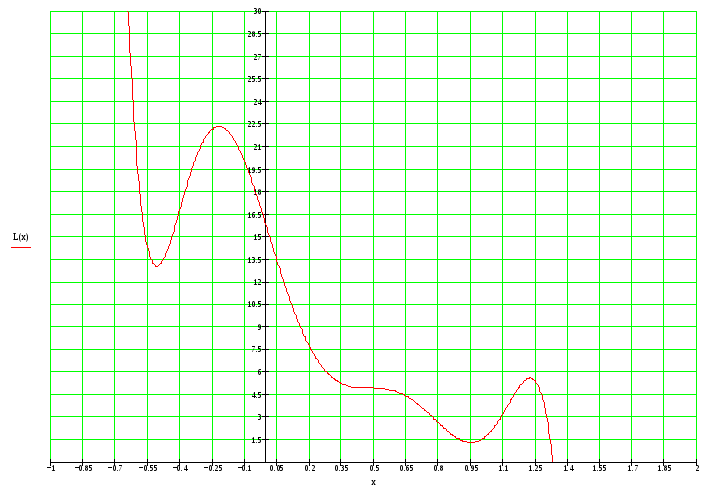
Построить его график и отметить на нем все узловые точки и по одной промежуточной для каждого интервала между узловыми точками.
|
Исходные данные |
|
|
x |
y |
|
-0,64 |
29,51 |
|
-0,36 |
18,86 |
|
0,08 |
12,05 |
|
0,2 |
7,7 |
|
0,48 |
4,92 |
|
0,76 |
3,14 |
|
1,04 |
2,01 |
|
1,32 |
1,28 |
Интерполяционный многочлен Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n+1 пар чисел (x0, y0), (x1, y1),…, (xn, yn), где все xj различны, существует единственный многочлен L(x) степени не более n, для которого L(xj) = yj.
В простейшем случае (n=1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.
Лагранж предложил способ вычисления таких многочленов:
![]()
где базисные полиномы определяются по формуле:
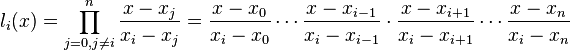
li(x) обладают следующими свойствами:
являются многочленами степени n
li(xi) = 1
li(xj) = 0 при j ≠ i
Отсюда следует, что L(x), как линейная комбинация li(x), может иметь степень не больше n, и L(xi) = yi.
Формула для вычисления полинома Лагранжа.
Для нахождения интерполяционного многочлена L(x) степени m, принимающего в (m + 1)-й заданной точке xi промежутка [a; b] заданные значения f(xi), i = 0, 1, 2, …, m.
Формула имеет вид:
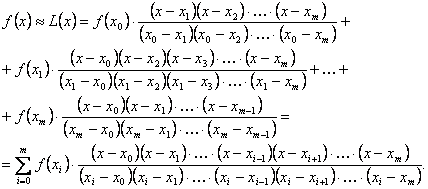
Легко видеть, что при подстановке в формулу значения х = хi все члены суммы, кроме i-го, обращаются в нуль (в числителе дробей, входящих в эти члены, появляются множители, равные нулю), а в i-м члене числитель становится равным знаменателю и дробь обращается в единицу, так что остается лишь множитель f(xi), т.е. получается, что L(xi) = f(xi).
Таким образом, интерполяционный многочлен Лагранжа совпадает в заданных точках с заданными значениями неизвестной функции.
Каким образом построить базисные полиномы?
Определим
![]() , i=0,
1,..., N.
, i=0,
1,..., N.
Легко понять, что
![]() ,
и т.д.
,
и т.д.
Функция li(z) является полиномом N–й степени от z и для нее выполняются условия "базисности":
![]() =0, i≠k;,
т.е. k=1,…,i-1
или k=i+1,…,N.
=0, i≠k;,
т.е. k=1,…,i-1
или k=i+1,…,N.
![]() .
.
Организуем вычисления в табличном процессоре Excel. Заполнение таблицы начинается с того, что вычисляются и заносятся в соответствующие клетки все элементарные разности. Вслед за этим вычисляются произведения Pi разностей по строкам:
P0=(x-x0)(x0-x1)(x0-x2)(x0-x3);
P1=(x1-x0)(x-x1)(x1-x2)(x1-x3); и т.д.
|
x |
x0 |
x1 |
x2 |
x3 |
Pi |
yi |
yi/Pi |
|
x0 |
x-x0 |
x0-x1 |
x0-x2 |
x0-x3 |
|
|
|
|
x1 |
x1-x0 |
x-x1 |
x1-x2 |
x1-x3 |
|
|
|
|
x2 |
x2-x0 |
x2-x1 |
x-x2 |
x2-x3 |
|
|
|
|
x3 |
x3-x0 |
x3-x1 |
x3-x2 |
x-x3 |
|
|
|
|
|
|
|
|
|
|
|
S=Σ(yi/Pi) |
Как мы видим из формулы, обозначение Pi – знаменатель в формуле Лагранжа, т.е.
![]() (i=0, 1, ... n).
(i=0, 1, ... n).
С учетом этого обозначения формула Лагранжа имеет вид
![]()
Все необходимые значения последовательно получаются в таблице. Сумма S образуется сложением элементов последнего столбца. Для получения окончательного значения Ln(x) достаточно умножить S на произведение Пn+1(х) (произведение диагональных разностей таблицы).
С помощью этой таблицы мы получим значения коэффициентов при вспомогательных многочленах (yi/Pi).
Таблица для расчета коэффициентов при многочленах в формуле Лагранжа, выполнена в Excel
|
x |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
Pi |
Yi |
Yi/Pi |
|
x0 |
0 |
-0,28 |
-0,72 |
-0,84 |
-1,12 |
-1,4 |
-1,68 |
-1,96 |
-0,87434 |
29,51 |
-33,7511041 |
|
x1 |
0,28 |
0 |
-0,44 |
-0,56 |
-0,84 |
-1,12 |
-1,4 |
-1,68 |
0,152663 |
18,86 |
123,5402078 |
|
x2 |
0,72 |
0,44 |
0 |
-0,12 |
-0,4 |
-0,68 |
-0,96 |
-1,24 |
-0,01231 |
12,05 |
-978,9461567 |
|
x3 |
0,84 |
0,56 |
0,12 |
0 |
-0,28 |
-0,56 |
-0,84 |
-1,12 |
0,008327 |
7,7 |
924,6956167 |
|
x4 |
1,12 |
0,84 |
0,4 |
0,28 |
0 |
-0,28 |
-0,56 |
-0,84 |
-0,01388 |
4,92 |
-354,5066832 |
|
x5 |
1,4 |
1,12 |
0,68 |
0,56 |
0,28 |
0 |
-0,28 |
-0,56 |
0,026215 |
3,14 |
119,7795178 |
|
x6 |
1,68 |
1,4 |
0,96 |
0,84 |
0,56 |
0,28 |
0 |
-0,28 |
-0,08327 |
2,01 |
-24,1381583 |
|
x7 |
1,96 |
1,68 |
1,24 |
1,12 |
0,84 |
0,56 |
0,28 |
0 |
0,602324 |
1,28 |
2,1251009 |
|
|
|
|
|
|
|
|
|
|
|
S= |
-221,2016591 |
Формулы в таблице:
|
x |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
Pi |
Yi |
Yi/Pi |
|
x0 |
=A16-$A$16 |
=A16-$A$17 |
=A16-$A$18 |
=A16-$A$19 |
=A16-$A$20 |
=A16-$A$21 |
=A16-$A$22 |
=A16-$A$23 |
=ПРОИЗВЕД(C4:I4) |
29,51 |
=K4/J4 |
|
x1 |
=A17-$A$16 |
=A17-$A$17 |
=A17-$A$18 |
=A17-$A$19 |
=A17-$A$20 |
=A17-$A$21 |
=A17-$A$22 |
=A17-$A$23 |
=ПРОИЗВЕД(B5;D5:I5) |
18,86 |
=K5/J5 |
|
x2 |
=A18-$A$16 |
=A18-$A$17 |
=A18-$A$18 |
=A18-$A$19 |
=A18-$A$20 |
=A18-$A$21 |
=A18-$A$22 |
=A18-$A$23 |
=ПРОИЗВЕД(B6:C6;E6:I6) |
12,05 |
=K6/J6 |
|
x3 |
=A19-$A$16 |
=A19-$A$17 |
=A19-$A$18 |
=A19-$A$19 |
=A19-$A$20 |
=A19-$A$21 |
=A19-$A$22 |
=A19-$A$23 |
=ПРОИЗВЕД(B7:D7;F7:I7) |
7,7 |
=K7/J7 |
|
x4 |
=A20-$A$16 |
=A20-$A$17 |
=A20-$A$18 |
=A20-$A$19 |
=A20-$A$20 |
=A20-$A$21 |
=A20-$A$22 |
=A20-$A$23 |
=ПРОИЗВЕД(B8:E8;G8:I8) |
4,92 |
=K8/J8 |
|
x5 |
=A21-$A$16 |
=A21-$A$17 |
=A21-$A$18 |
=A21-$A$19 |
=A21-$A$20 |
=A21-$A$21 |
=A21-$A$22 |
=A21-$A$23 |
=ПРОИЗВЕД(B9:F9;H9:I9) |
3,14 |
=K9/J9 |
|
x6 |
=A22-$A$16 |
=A22-$A$17 |
=A22-$A$18 |
=A22-$A$19 |
=A22-$A$20 |
=A22-$A$21 |
=A22-$A$22 |
=A22-$A$23 |
=ПРОИЗВЕД(B10:G10;I10) |
2,01 |
=K10/J10 |
|
x7 |
=A23-$A$16 |
=A23-$A$17 |
=A23-$A$18 |
=A23-$A$19 |
=A23-$A$20 |
=A23-$A$21 |
=A23-$A$22 |
=A23-$A$23 |
=ПРОИЗВЕД(B11:H11) |
1,28 |
=K11/J11 |
|
|
|
|
|
|
|
|
|
|
|
S= |
=СУММ(L4:L11) |
Из таблицы мы имеем значения коэффициентов для вспомогательных многочленов (Yi/Pi)
Для построения всех многочленов используем систему MathCad. Упрощение выражения выполнение с помощью функции expand (разложение).
Умножим вспомогательные многочлены на коэффициенты yi/Pi предварительно.
Интерполяционный
многочлен Лагранжа является суммой
всех многочленов.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
