4. Нахождение вспомогательного вектораY.

Для нахождения вектора Y мы решаем систему S^tY=B, и получаем:

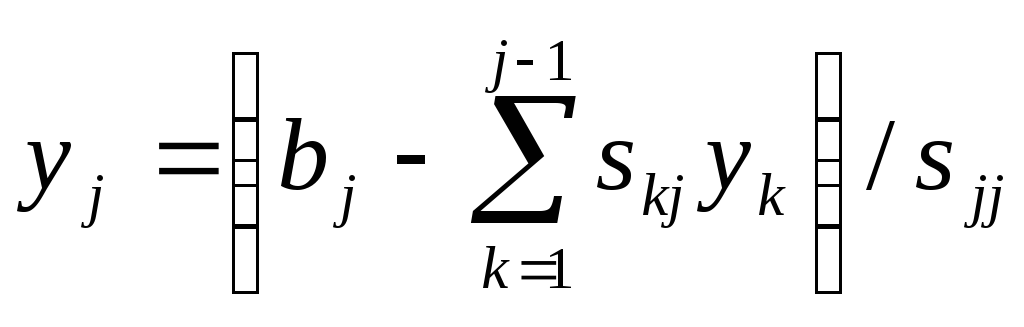, где j=1,2,...,n

5. Нахождение вектора решения х.

Для нахождения вектора Х мы решаем систему SХ=Y, и получаем:

, где i=n,n-1,...,1

6. Пример.

Решим с помощью метода квадратного корня следующую систему:

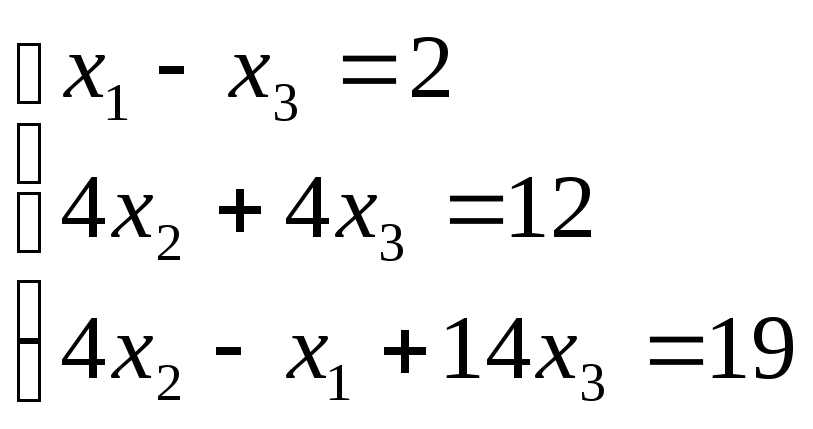или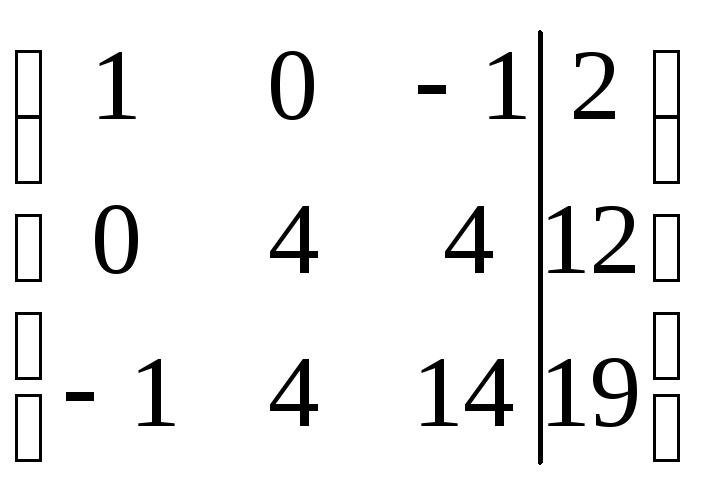

Заметим, что условие симметричности: выполняется, но если поделить второе уравнение на 4, то оно перестанет выполняться и метод квадратного корня применять будет уже нельзя.

1. Вычисляя по формулам коэффициенты матрицы S, получим:

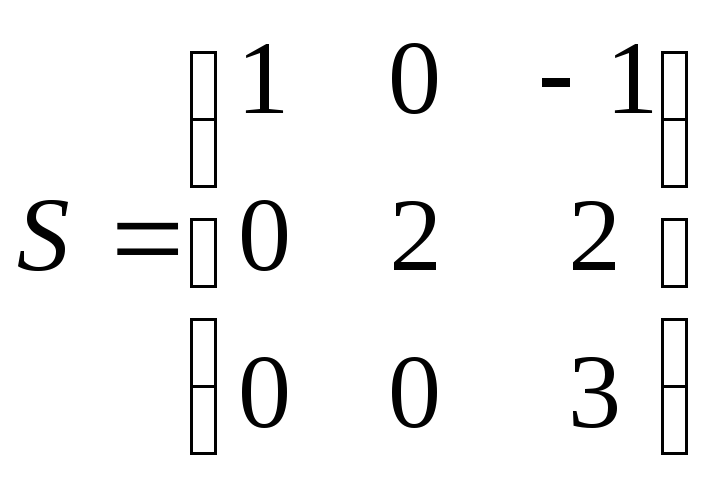и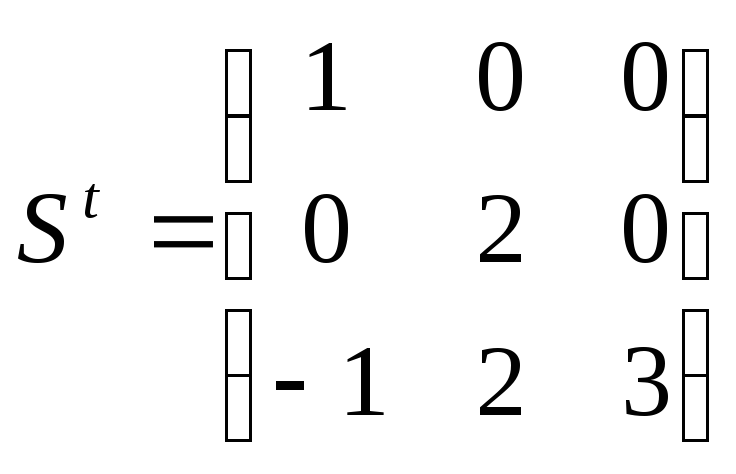

2. Находим координаты вспомогательного вектора:

,откуда получаем

1. Находим решение:

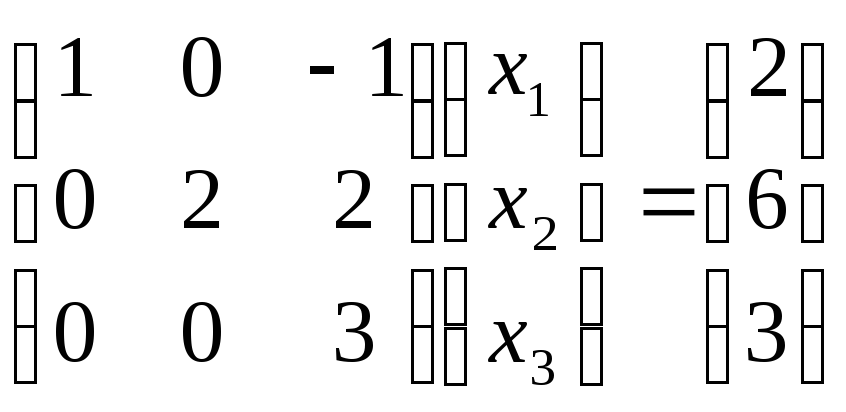,откуда получаем

2. На всякий случай, подставляя Х в исходную систему, убеждаемся в правильности решения.

7. Компакт-метод.

Как уже отмечалось, метод квадратного корня применим только для систем с симметричной матрицей A. Однако существует так называемый компактный метод, который по сути очень похож на метод квадратного корня, но применим уже к любым невырожденным квадратным системам. При этом суть метода остается той же - разложение матрицы A на произведение верхне-и нижнетреугольной матриц, правда уже не взаимнотранспонированных.

Упражнение 8.1. Вывести самостоятельно матричное описание компакт-метода.

Упражнение 8.2. Вывести самостоятельно формулы для разложения матрицы А системы на произведение верне- и нижнетреугольной матриц.

1. Контрольные вопросы.

1. Что такое транспонированная матрица, симметрическая матрица?

2. Что такое главные миноры? Бывают ли главные миноры у неквадратной матрицы?

3. Какая матрица называется положительно определенной?

4. Каковы условия применимости метода квадратного корня?

5. Что может получиться, если применять метод к симметрическим, невырожденным, но не положительно определенным матрицам?

6. Что может получиться, если применять метод к несимметрическим матрицам?

7. Опишите в матричном виде процесс решения системы данным методом.

8. Почему при поиске элементов матрицы S мы выписываем 10, а не все 16 уравнений?

1. Содержание лабораторной работы.

1. Ответить на вопросы контролирующей программы.

2. Составить, отладить и протестировать на контрольных примерах программу решения систем линейных уравнений методом квадратного корня.

3. Попробовать применить программу к системам, где метод квадратного корня не применим. Дополнить программу проверкой применимости метода.

4. (дополнительно). Составить программу для решения систем компакт-методом.

5. Составить отчет, содержащий цель и назначение работы, постановку задачи, текст программ и варианты исполнения для своих данных.

9. Метод простых итераций

Данный метод относится к приближенным методам решения систем линейных уравнений. Для его применения необходимо преобразовать исходное уравнение АХ=В к эквивалентному виду Х=АХ+В, (9.1)

где матрица А и вектор В не те, что были в исходной задаче, и должны удовлетворять некоторым условиям, чтобы метод итераций давал последовательность векторов, сходящуюся к решению. Ясно, что для такого преобразования матрица А должна быть квадратной.

Упражнение 9.1. Обоснуйте.

Мы будем рассматривать уравнение (9.1) при условии, что его решение существует и единственно, т.е. будем рассматривать только корректную задачу.

Упражнение 9.2. Сформулируйте краткое математическое условие на матрицу А, при котором уравнение (9.1) имеет единственное решение для любого вектора В.

Так же, как метод итераций для обычных уравнений и метод Пикара для дифференциальных уравнений, метод простых итераций для систем линейных уравнений является следствием из общего принципа сжимающих отображений.