Вопросы для допуска к выполнению лабораторной работы

1. Как можно зарядить диэлектрическое тело?

2. Сформулируйте закон сохранения заряда.

3. Как можно зарядить электрометр? Почему стрелка заряженного электрометра отклоняется?

4. В чём заключается явление электростатической индукции?

5. Дайте определение напряжённости электростатического поля . Чему равна напряжённость поля плоского конденсатора?

6. Дайте определение потенциала электростатического поля φ. Чему равен потенциал уединённого заряженного шара?

7. Что такое ёмкость проводника? Конденсатора? От чего она зависит? В каких единицах измеряется?

9. Опишите методику определения ёмкости установки; проводника.

Контрольные вопросы

1. Что называется ёмкостью проводника? Конденсатора?

2. Сформулируйте теорему Остроградского-Гаусса. С её помощью получите выражения для напряжённости поля сферического и цилиндрического конденсаторов.

3. Выведите формулу для ёмкости уединённого шара.

4. Как связаны между собой потенциал и напряжённость электростатического поля?

5. Выведите формулу для ёмкости плоского конденсатора; сферического конденсатора; цилиндрического конденсатора.

6. Нарисуйте последовательно и параллельно соединённые конденсаторы. Докажите формулы для общей ёмкости батареи в этих случаях.

Таблица 5.5

Зависимость напряжения от угла отклонения стрелки электрометра

α, дел.	U, В	α, дел.	U, В	α, дел.	U, В	α, дел.	U, В	α, дел.	U, В	α, дел.	U, В
3	20	15	280	27	550	39	870	51	1300	63	2110
4	30	16	300	28	580	40	900	52	1340	64	2220
5	50	17	320	29	600	41	930	53	1390	65	2330
6	75	18	340	30	620	42	860	54	1440	66	2460
7	110	19	360	31	650	43	990	55	1490	67	2600
8	130	20	390	32	680	44	1030	56	1550	68	2760
9	150	21	410	33	700	45	1070	57	1620	69	2950
10	180	22	430	34	730	46	1100	58	1690	70	3250
11	200	23	455	35	760	47	1130	59	1750
12	220	24	480	36	790	48	1170	60	1850
13	240	25	500	37	820	49	1200	61	1940
14	260	26	520	38	840	50	1260	62	2020

Используемая литература

[1] §§ 13.1; 13.3; 13.4; 14.1;16.2;16.3;

[2] §§ 10.8 – 10.10; 10.13; 11.4 – 11.6;

[3] §§ 1.5;1.6; 1.13; 3.2 – 3.4;

[4] §§ 79; 81;82;85; 86; 93; 94.

Лабораторная работа 2-06

Изучение процессов заряда и разряда конденсатора (ФПЭ-08)

Цель работы: изучение заряда и разряда конденсатора при различных параметрах емкости и сопротивления электрической цепи и вычисление времени релаксации.

Теоретическое введение

В работе рассматривается процесс накопления заряда на конденсаторе С (т.е. его зарядка от источника напряжения) и релаксация этого заряда (т.е. разряд конденсатора) в цепи сопротивлением R.

Электрическая цепь содержит последовательно соединенные конденсаторС, сопротивление R и источник ЭДС ε (рис. 6.1). Первоначально конденсатор не заряжен. Пусть I, U – мгновенные значения тока и разности потенциалов между обкладками конденсатора, q – заряд конденсатора. Полагаем, что токи и напряжения удовлетворяют условиям квазистационарности, т.е. мгновенное значение тока во всех сечениях провода и элементах цепи одно и то же, и соотношение между мгновенными значениями I, q и U такое же, как и в цепи постоянного тока. В момент времени t=0 ключ К замкнули, и в цепи пошел ток, заряжающий конденсатор:

. (6.1)

Применим второе правило Кирхгофа к цепи (рис.6.1):

, (6.2)

где R – полное сопротивление цепи, включающее внутреннее сопротивление источника тока, U – разность потенциалов (падение напряжения) на пластинах конденсатора:

. (6.3)

Из (6.1)÷(6.3) получим дифференциальное уравнение для заряда конденсатора:

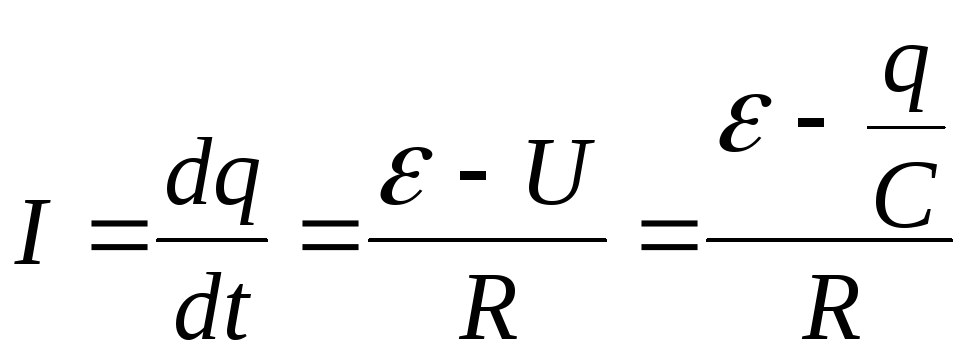
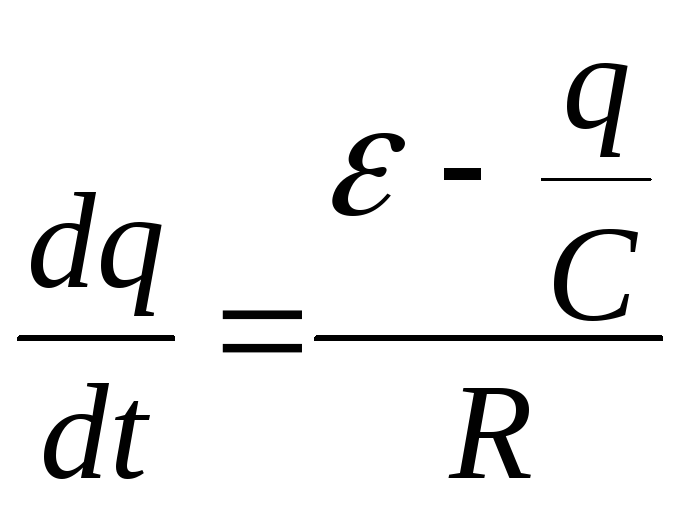, (6.4)

Разделим переменные и проинтегрируем это уравнение с учетом начального условия: при t=0 заряд q=0:

,

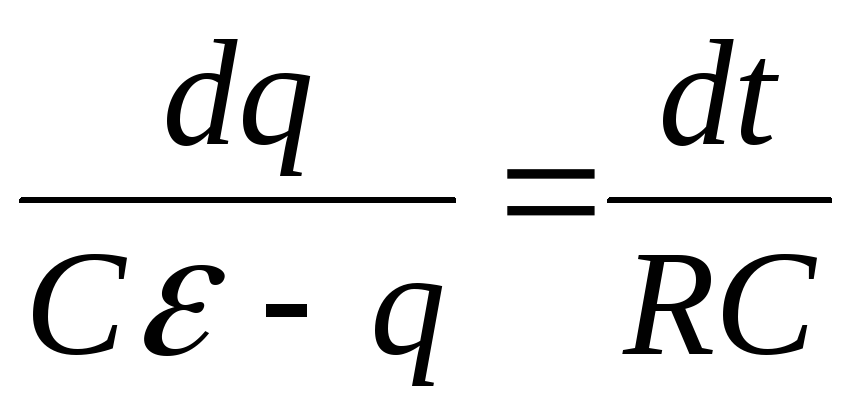
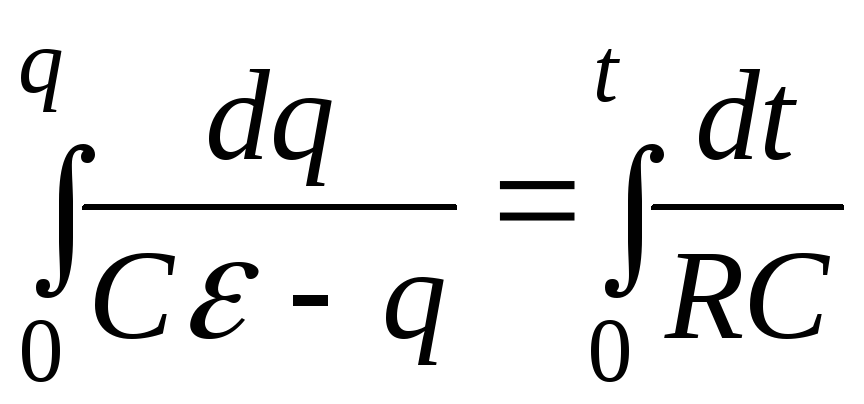
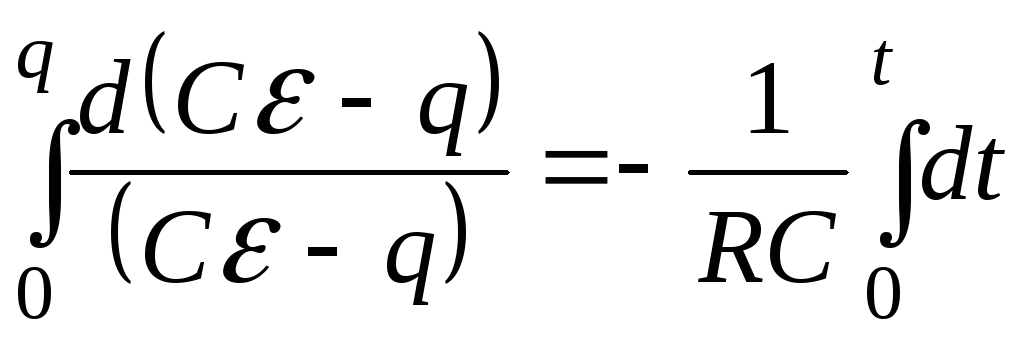
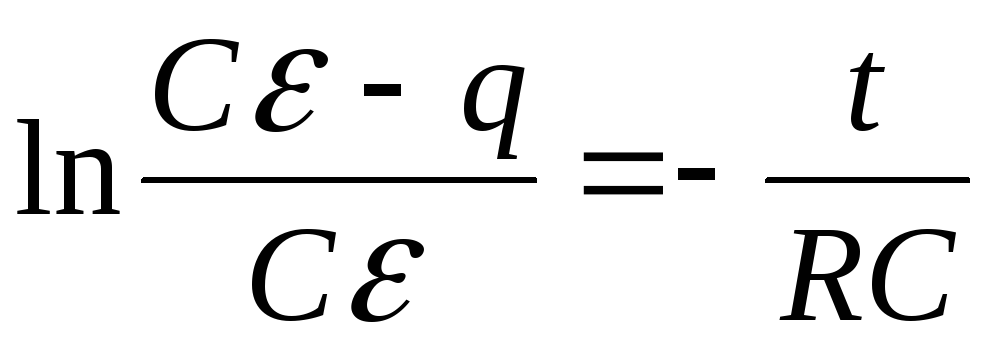
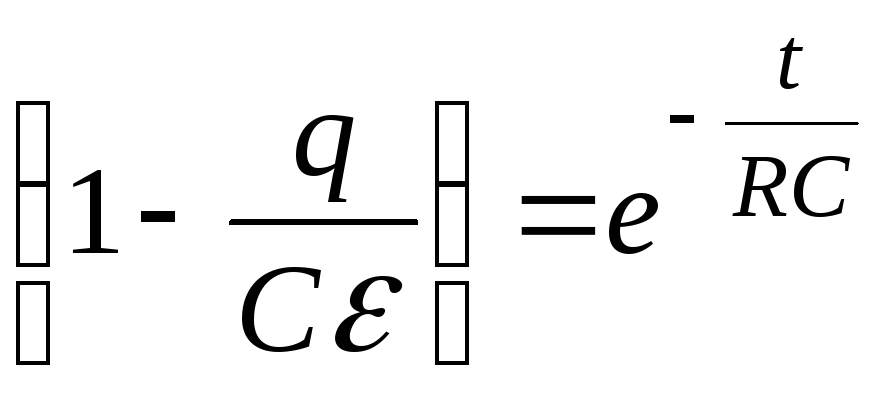
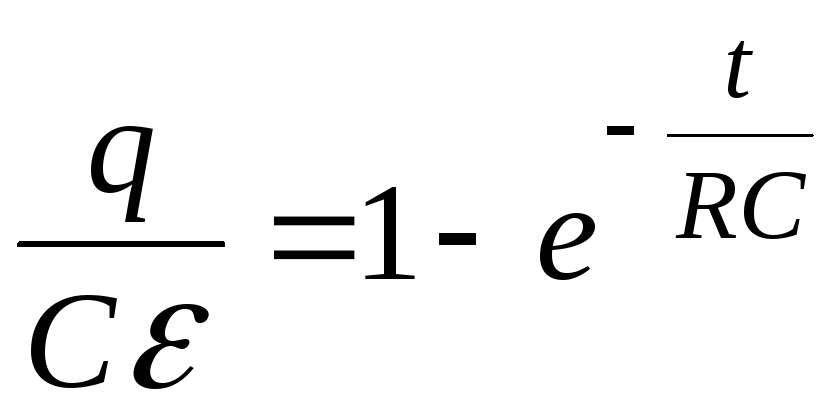, (6.5)

гдеq₀=εC – предельное значение заряда на конденсаторе.

Напряжение на конденсаторе изменяется по закону

.

Закон изменения тока в цепи получим дифференцированием:

, (6.6)

где .

Графики зависимостей q(t), U(t) и I(t) представлены на рис. 6.2.

Рассмотрим процесс разряда конденсатора емкостью С, пластины которого замкнуты сопротивлением R. По второму правилу Кирхгофа для контура рис.6.3, аналогично уравнению (6.4), получим: , откуда

. (6.7)

Разделяем переменные и интегрируем с учётом граничного условия, что в момент времени t=0 заряд конденсатора равен q=q₀:

(6.8)

; ; ;

; ;

. (6.9)

Закон изменения напряжения на конденсаторе в процессе разряда аналогичен:

, (6.10)

где

.

Графики зависимостей q(t) и U(t) приведены на рис. 6.4. Эти функции являются экспоненциальными.

Произведение RС имеет размерность времени и называется постоянной времени, или временем релаксации :

. (6.11)

За время заряд конденсатора уменьшается в e раз (e≈2.7 – основание натурального логарифма). Для определения RС часто удобно измерять время, за которое величина заряда падает до половины первоначального значения, так называемое "половинное время" t_1/2. "Половинное время" определим из (6.9), подставив :

. (6.12)

Берём натуральный логарифм от обеих частей уравнения (6.12):

,

. (6.13)

Способ измерения постоянной времени состоит в определении t_1/2 и умножении полученной величины на 1.44. Так как экспонента асимптотически приближается к оси абсцисс, то точно установить окончание процесса разряда конденсатора (так же как и процесса заряда) не представляется возможным. Поэтому целесообразно изме­рять время уменьшения величины заряда в 2 раза, т.е. “половинное время”. За каждый интервал времени напряжение на конденсаторе уменьшается в два раза (рис. 6.4).

Кроме того, постоянную времени можно найти графическим способом. Из формулы (6.10) находим:

, (6.14)

Логарифмируя левую и правую части (6.14), получаем

. (6.15)

Построив логарифмическую зависимостьy=f(x), где , а, получим прямую, котангенс угла наклона которой к оси Х есть характеристическое время релаксации заряда, или постоянная времениRC:

. (6.16)

Если обкладки конденсатора попеременно подключать к источнику тока и к сопротивлению R (рис. 6.5), то график процесса заряд-разряд конденсатора будет иметь вид, показанный на рис. 6.6. Процесс заряда-разряда можно наблюдать с помощью осциллографа, подавая на вход Y напряжение с конденсатора C.