69
Основным достоинством решетчатой структуры является то, что она измеряет на обратных разностных выходах автокорреляцию сигнала при последовательно возрастающих задержках для получения на выходе серии информационно зависимых ортогональных выборок сигналов, которые затем можно использовать для подачи на взвешивающий комбинатор обобщенной структуры Чанга.
5.8.1. Фильтр Винера-Хопфа.
Концепции оптимального линейного оценивания являются фундаментальными при любом рассмотрении адаптивных фильтров. Процесс адаптивной фильтрации включает два этапа проведения оценивания: 1) оценивание искомого выхода фильтра и 2) оценивание весов фильтра, необходимых для достижения вышеупомянутой цели. Второй из этих двух этапов необходим вследствие того, что в случае адаптивной фильтрации характеристики входного сигнала априорно не известны.
Наиболее широко распространенным типом структуры адаптивного фильтра является структура, в которой используется архитектура с конечной импульсной характеристикой (КИХ). Эти фильтры должны сходится к решению с помощью оптимального нерекурсивного устройства оценки, причем решение задается уравнением Винера – Хопфа [23].
Синтез КИХ и БИХ устройств оценки существенно зависит от определения стоимостной функции, в соответствии с которым качество оценивания характеризуется разностью между выходным сигналом устройства оценки и истинным параметром, подлежащим оцениванию:
e(n) |
= |
x(n) |
x(n) . |
(5.22) |
|
|
− € |
|
Здесь e(n) – ошибка оценивания; x(n) – случайная величина, которую необ-
ходимо оценить и которая может быть детерминированной, а x(n) – оценка |
x(n) , |
|||
|
|
|
€ |
|
выполненная с помощью нашей системы оценивания, причем |
|
|
||
x(n) |
= |
f {y(n),h(n)}, |
(5.23) |
|
€ |
|
|
|
|
т.е. x(n) – линейная функция последовательности входных сигналов y(n) и набора весов фильтра h(n). Наблюдаемую последовательность сигналов y(n) в общем виде можно представить как исходную последовательность x(n), иска-
женную адаптивным белым шумом v(n )с дисперсией σv2: |
(5.24) |
|||
|
y(n) = x(n) + v(n) . |
|||
Наиболее |
употребительным при проведении оптимального |
оценивания |
||
x(n) является |
метод наименьших квадратов (МНК). Среднеквадратическая |
|||
€ |
|
|
|
|
ошибка определяется как |
|
|||
|
|
|
. |
(5.25) |
|
E{e2 (n)} = [x(n) − x€(n)]2 |
|||
Она минимизируется относительно весовых коэффициентов устройства оценки для получения оптимального оценивания по критерию МНК. Следует отметить, что можно применять не только описанную функцию стоимости. Альтернативными будут такие функции, как абсолютная величина ошибки и нелинейная пороговая функция. Такая функция ошибки используется в том случае, когда имеется приемлемый интервал ошибок (т.е. существует заданная
70
допустимая ошибка). При использовании критерия наименьшего среднеквадратичного малые ошибки вносят меньший вклад, чем большие ошибки (в противоположность критерию абсолютной величины ошибки, который дает одинаковый вес для всех ошибок).
y(n) 
Z-1 
Z-1 
Z-1 
Z-1
h X h X h X |
hN- X |
∑ 
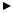x€(n)
Рис. 5.9. Обобщенный нерекурсивный фильтр или устройство оценки.
В нерекурсивном устройстве оценки оценка x(n) определяется в виде конечного линейного полинома y(n):
x(n) |
|
N −1 |
|
k)hk , |
(5.26) |
= |
∑y(n |
− |
|||
€ |
|
|
|
k =0
где hk – отдельные веса в структуре нерекурсивного фильтра КИХ-типа, показанного на рис. 5.9. Выражение (5.28) можно переписать в матрично-векторной системе обозначений:
x(n) |
|
Y |
|
(n)H |
|
H |
|
Y (n) , |
(5.27) |
€ |
= |
|
T |
|
= |
|
T |
|
|
где |
|
|
|
|
|
|
|
|
|
YT (n) =[y(n)y(n −1)...y(n − N −1)] и |
H T =[h0h1h2...hn−1] , |
||||||||
а верхний индекс Т обозначает транспонирование матрицы. Тогда функция среднеквадратичной ошибки принимает вид
E{e2 (n)} = E{x(n) − H TY (n)}2 . |
(5.28) |
Это выражение описывает стандартную поверхность квадратичной ошибки с одним единственным минимумом. Дифференцирование (5.30) по H T дает
∂e2 (n) |
= −2E[{x(n) − H TY (n)}Y T (n)] . |
(5.29) |
∂H T |
|
|
а допуская, что (5.31) равно нулю, имеем
E[{x(n) − H TY (n)}Y T (n)] = 0 |
(5.30) |
|
E{x(n)Y T (n)} = E{H TY (n)Y T |
||
(n)}. |
Полагая, что весовой вектор H T и вектор сигнала Y(n) не коррелированы, получаем
E{x(n)Y T (n)} = H T opt E{Y (n)Y T (n)}. |
(5.31) |
Члены математического ожидания, входящие в (5.33), можно определить следующим образом: