39

4. ПЕРЕХОД ОТ АНАЛОГОВЫХ СИГНАЛОВ К ЦИФРОВЫМ

Переход от непрерывных аналоговых сигналов к цифровым осуществляется с помощью процедур дискретизации и квантования, выполняемых последовательно друг за другом. Их совместное применение называют аналого-цифровым преобразованием [19,20].

Процесс перехода от непрерывной области изменения аргумента (задания функции) к конечному множеству отдельных значений аргумента называется дискретизацией.

Процесс перехода от непрерывной области изменения функции к конечному множеству определенных значений называется квантованием.

4.1. Дискретизация сигналов

Дискретизация аналогового сигнала может осуществляться тремя способами:

1)как процедура выбора отсчетов сигнала в фиксированные моменты времени, следующие через равные промежутки времени t (интервал t называют шагом дискретизации, а

обратная величина fD = 1/ t носит название частоты

дискретизации), такой способ носит название равномерной дискретизации;

2)как процедура выбора отсчетов сигнала в моменты времени, следующие друг за другом через не равные интервалы времени ( чаще всего величину интервала выбирают в зависимости от скорости изменения сигнала на различных интервалах), так называемая адаптивная дискретизация;

3)как процедура выбора отсчетов в фиксированные моменты времени, задаваемые случайным образом по тому или иному закону (стохастическая дискретизация).

Простейшим случаем является дискретизация с равномерным шагом, поэтому на практике такой способ применяется наиболее широко.

Переход от непрерывного сообщения к дискретному осуществляется с потерей информации. Восстановление непрерывного сигнала по дискретным значениям на приемной стороне и устранение потерь информации зависит от

40

Возможны три различных ситуации при восстановлении сигнала после дискретизации:

а) fS < fN – возможно правильное восстановление сигнала

б) fS = fN – восстановленный сигнал по дискретным отсчётам будет

иметь ту же частоту, что и до дискретизации, однако фаза и амплитуда сигнала могут быть искажены.

в) fS > fN – восстановленный сигнал так же будет гармоническим, но

его частота будет иной. Иначе говоря, проявляется эффект появления ложных частот (aliasing).

Отсюда следует, что при дискретизации возможны искажения, связанные с потерей информации о величине сигнала вне моментов измерения отсчетов.

Рассмотрим вначале спектр дискретного сигнала. Пусть сигнал имеет вид:

∞ ∞

S(t) = ∑ xkδ(t −tk ) = ∑ xkδ(t − k∆t)

k=−∞ k=−∞

Такому дискретному сигналу соответствует спектральная плотность, описываемая как

∞

S(ω) = ∑ xk e− jωk∆t . k=−∞

При этом учтены следующие факторы:

1)спектр δ -функции равен 1

2)задержка сигнала во времени на k∆t приводит к умножению сигнала на комплексную экспоненту ( см. раздел 2.5).

Важнейшее свойство спектра дискретного сигнала является его периодичность с периодом 2π , т.е.

Это свойство иллюстрируется на рис.4.1.

ω∂

Рис.4.1. Амплитудный спектр дискретного сигнала.

Однако согласно теории Фурье-анализа конечной апериодической функции f(x) соответствует бесконечный спектр и наоборот, конечный спектр соответствует бесконечной исходной функции.

Поэтому для реальных сигналов условия теоремы Котельникова в строгом смысле слова не выполняются.

1.Все реальные сигналы ограничены во времени и имеют неограниченный спектр, т.е. fв= .

2.В соответствии с рядом Котельникова восстановление осуществляется по бесконечному числу отсчетов (- ≤ k ≤ ).

3.Поскольку сигнал восстанавливается по бесконечному числу отсчетов

функций, то его восстановление осуществляется с бесконечной задержкой во времени.

Несмотря на эти недостатки, теорема Котельникова имеет фундаментальное значение, так как позволяет определить предельные возможности дискретной передачи сигналов.

Пример.

Передается речевой сигнал в полосе частот ∆F (от 0 до 3000 Гц). Время передачи ∆t = 10 сек. Каждый дискретный отсчет кодируется 5 двоичными разрядами.

Определить минимальный объем памяти, требуемый для хранения информации Wзу .

T=1/2∆F=1/6000=0,00016 с.,

следовательно, число отсчетов на интервале ∆t: N=∆t/T=10/0,00016=60000.

Объем ЗУ: Wзу =60000 × 5 = 300000 бит.

На практике теорему Котельникова для выбора шага дискретизации применяют следующим образом:

1.Определяют эффективную ширину спектра fэ.

2.Вычисляют шаг дискретизации T=1/2fэ.

3.На приемной стороне восстанавливается сигнал по следующей формуле

где Т - длительность сигнала; ∆t - шаг дискретизации; β =∆t/Т - база сигнала.

Итак, в результате дискретизации в соответствии с теоремой Котельникова от x(t) мы переходим к набору отсчетов или к вектору:

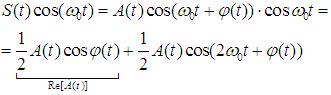
44

4.1.3. Дискретизация при использовании квадратурных сигналов

Пусть сигнал имеет вид:

S(t) = A(t)cos(ω0t +ϕ(t)),

где ω0 – несущая частота, A(t) и ϕ(t) – законы амплитудной и фазовой апяции, которые задают медленно (по сравнению с cos(ω0t)) меняющиеся функции.

Если непосредственно из теоремы Котельникова выбирать частоту дискретизации, то она должна быть не меньше, чем ω0 + ω , где ω – ширина

спектра сигнала S(t).

Однако такой сигнал можно представить, перейдя к комплексному виду,

как:

S(t) = A(t) e jϕ(t) e jω0t

Информация, переносимая сигналом, описывается как:

A(t) = A(t) e− jϕ(t)

Умножим S(t) на cos(ω0t) в одном канале и на sin(ω0t) – в другом

(рис.4.3).:

S(t)sin(ω0t) = −12 Im(A(t)) − 12 A(t)cos(2ω0t −ϕ(t))

В результате получаем частоту дискретизации ω . Такой принцип дискретизации называют гетеродинированием сигнала [19].

45

sin(ω0t)

Рис.4.3. Принцип дискретизации с гетеродинированием сигнала

4.1.4. Определение шага временной дискретизации при восстановлении сигнала полиномами 0-го порядка

Восстановление по непрерывного сигнала по теореме Котельникова связано с задержкой сигнала, что неприемлемо в системах работающих в реальном масштабе времени.

Для восстановления сигнала в реальном масштабе времени необходимы способы восстановления с экстраполяцией (предсказанием) сигнала. При этом могут использоваться полиномы различной степени. Простейший полином - 0-й степени. Рассмотрим этот случай (рис. 4.4.).

x(t)

t

T

Рис. 4.4.

Требуется определить интервал времени Т, при котором погрешность восстановления не превышает допустимых пределов, т.е. σв ≤ (σв)допуст.

Для этого необходимо знать:

1.Наибольшее значение сигнала по модулю - x max.

2.Эффективную ширину спектра сигнала fэ.

Надо на основании ∆х определить σв.

σв = D в;

∞

Dв = ∫ωв(x)x2 dx,

−∞

где Dв -дисперсия; ωв(х) - закон распределения плотности вероятности погрешности дискретизации; х - параметр интегрирования. Рассмотрим равномерный закон распределения. В этом случае (см. раздел

σΒ = ∆3x . (4.6)

Подставляя (4.6) в (4.5) получим

47

T = 3σв .

2 x max π fэ

Методика выбора шага дискретизации Т.

1. По заданному значению x max и fэ при помощи неравенства Бернштейна

•

определяем x .

max

2. По заданной величине (σв)допуст определяем наибольшее отклонение сигнала за время Т ∆x = σв 3.

3. Определяем требуемый шаг T = •∆x .

x

max

4.1.5. Определение шага дискретизации при заданной автокорреляционной функции

Рассмотрим рисунок

Из рисунка видно, что ошибка e(t)=y(t)-x(t)=x(t-T)-x(t)=x(t*)-x(t*-T)=x(t)-x(t+T). Введено обозначение

t*=t-T.

Дисперсия этой ошибки

− 2lim 1 ∫T [x(t)x(t +T)]dt.

T→∞ T 0