Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Функан расчет

.pdf

Скачиваний:

Добавлен:

21.03.2016

Размер:

351.04 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ

И.В.Блинова, И.Ю. Попов, Е.С.Трифанова ТИПОВЫЕ РАСЧЕТЫ

по функциональному анализу

Санкт-Петербург

2011

Блинова И.В., Попов И.Ю., Трифанова Е.С. Типовые расчеты по функциональному анализу. – СПб: СПбГУ ИТМО, 2011. – 24 с.

Методическое пособие содержит два типовых расчета по функциональному анализу. Предназначено для студентов третьего курса ЕНФ и ИТиП, обучающихся по направлению 01.04.00 (Прикладная математика и информатика).

Рекомендовано к печати Советом естественнонаучного факультета СПбГУ ИТМО 01.03.2011 (протокол № 2)

В 2009 году Университет стал победителем многоэтапного конкурса, в результате которого определены 12 ведущих университетов России, которым присвоена категория «Национальный исследовательский университет». Министерством образования и науки Российской Федерации была утверждена Программа развития государственного образовательного учреждения высшего профессионального образования «Санкт-Петербургский государственный университет информационных технологий, механики и оптики» на 2009–2018 годы.

©Санкт-Петербургский государственный университет информационных технологий, механики и оптики, 2011

©Блинова И.В., Попов И.Ю., ТрифановаЕ.С., 2011

Типовой расчет № 1 «Пространства и операторы»

I. Проверить, образует ли (X , ρ) метрическое пространство, если

X =C[a,b], ρ(x, y)=(∫ab (x(t) − y(t))2 dt )12 .

Решение. Для того чтобы определить, является ли данное пространство метрическим, нужно проверить, удовлетворяет ли заданная функция расстояния ρ(x, y), где x, y X трем аксиомам:

1)x, y X : ρ(x, y)≥ 0 , и ρ(x, y)= 0 x = y ;

2)x, y X : ρ(x, y)= ρ(y, x) (аксиома симметрии);

3)x, y, z X : ρ(x, z)≤ ρ(x, y)+ ρ(y, z) (аксиома треугольника).

Для данной функции ρ(x, y) выполнение условий 1) и 2) очевидно. Докажем выполнение аксиомы треугольника, которая примет вид

∫b (x(t) − z(t))2 dt ≤	∫b (x(t) − y(t))2 dt +		∫b (y(t) − z(t))2 dt .	(1)
a	a		a
Введем обозначения x(t )− y (t )= f (t ),		y(t )− z (t )= g (t ). Тогда неравенство
(1) примет вид
∫b ( f (t) + g(t))2 dt ≤	∫b f 2	(t )dt + ∫b g2	(t )dt .	(2)
a	a	a

Полученное неравенство следует из неравенства Коши-Буняковского:

(∫ab f (t )g (t )dt )2 ≤ ∫ab f 2 (t )dt ∫ab g2 (t )dt .

Имеем

∫b ( f (t) + g(t))2 dt =

∫b

f 2 (t)dt +∫b g2 (t)dt +2∫b f (t)g (t )dt ≤

g2 (t)dt + 2

f 2

f 2 (t)dt +

2 (t)dt

≤

∫a

(t)dt +

∫a

(t)dt

∫a

f 2

g2 (t)dt =

(3)

2 ,

что равносильно неравенству (2). Следовательно, все три аксиомы выполнены, и данное пространство является метрическим.

II. Проверить, можно ли ввести норму в пространстве X =l1 ,

x =(x1, x2 ,K, xn ,K) следующим образом: x =sup ∑xi .

n N i=1

Решение. Для того чтобы определить, может ли заданная функция являться

нормой в пространстве X , нужно проверить, удовлетворяет ли она трем условиям:

1) x X : x ≥ 0 , причем x = 0 x = 0 ;

2)x, y X : x + y ≤ x + y ;

3)x X , α : αx = α x .

Для данной функции выполнение условия 1) очевидно. Проверим выполнение условия 2). Воспользуемся свойствами модуля и супремума:

∑

∑ i

x + y

=sup

+ y

)

≤sup

+sup

i=1

n N

i=1

n N

i=1

n N

i=1

x, y X .

Условие 3) также выполнено:

		n		n
λx	=sup	∑λxi	=sup	λ∑xi
λx	=sup	∑λxi	=sup	λ∑xi
	n N	i=1	n N	i=1

= λ sup ∑xi = λ x , x X , α .

n N i=1

Следовательно, функция x =sup ∑xi задает норму на пространстве X .

n i=1

III. В пространстве Η найти проекцию элемента x на подпространство,

порожденное	f	, f	2	,K, f	n	, если Η = L	(0,1),	x =t2 , f =1 +t, f	2	= t.
	1		2		n	2		1	2

Решение. Обозначим Μ - подпространство, порожденное функциями f1, f2 . Тогда x(t )=ϕ(t )+ψ (t ), где ϕ Μ - проекция x на Μ , ψ Μ . Разложим функцию ϕ по базису f1, f2 :

ϕ(t )=α f1 (t )+ β f2 (t )

инайдем коэффициенты разложения α и β в этом базисе. Имеем

x(t )=α f1 (t )+ β f2 (t )+ψ (t ).

Умножим это равенство скалярно сначала на f1 , а затем на f2 :

(x, f

)=α

β ( f

, f

);

(4)

2 .

(x, f

)

=α( f ,

)+ β

Вычислим скалярные произведения, зная, что ( f , g )

= ∫1 f

(t )g

(t )dt . Имеем

(x, f

1t2 (1 +t )dt =

, (x, f

)= 1t2

tdt = 2 ,

∫0

( f

, f

)=( f , f

t (1 +t )dt =16

2 =

1(1 +t )2 dt = 7 ,

= 1tdt = 1 .

∫0

Для решения системы (4) воспользуемся формулами Крамера. Определители системы

	7	16		13			7		16		11			7	7			2
=	3	15	=		,	α =		12	15	= −		,	β =	3		12	=		.
				450							840							45
	16	1					2		1					16	2
	15	2					7		2					15	7

Тогда

α =

α = −165

, β =

= 20 .

364

И окончательно, ϕ(t )

= −165

(1 +t )

+ 20

t .

364

IV.

Показать, что

оператор

A :

(Af )(s) = ∫1

2s t2 f (t )dt ,

ограничен в

пространстве X =C[0,1], и найти его норму.

A . В пространстве C[a,b]

Решение. Докажем ограниченность оператора

норма элемента x равна

= sup

x(t )

= max

x(t )

Имеем

t [a,b]

a≤t≤b

= sup

∫12s t2 f (t )dt

s [0,1]

= sup 2s

∫1t2 f (t )dt

≤ 2∫1

f (t )

t2dt ≤

s [0,1]

∫1t2dt = 2

≤ 2∫1t2 sup

f (t )

dt ≤ 2 sup

f (t )

t [0,1]

при

f (t ) X . Следовательно, оператор A ограничен.

Норма оператора

A определяется следующим образом:

= sup

Tогда получаем

1 = 2 .

= sup max

∫1

2s t2 f (t )dt

= max 2s sup

∫1t2 f (t )dt

= 2

=1 0≤s≤1

0≤s≤1

3 3

V. Найти точечный спектр и собственные функции оператора A: Ay = y′′+ 2 y , заданного на дважды непрерывно дифференцируемых функциях с граничными условиями y′(0)= y (1)= 0 в пространстве L2 [0,1].

Решение. Запишем уравнение для определения собственных значений и собственных функций:

	Ay = λy ,
то есть	y′′+(2 −λ)y = 0 .			(5)
	y′′+(2 −λ)y = 0 .			(5)
Его решения будут разными в зависимости от знака выражения				λ −2 .
Рассмотрим 3 случая:
1) λ −2	> 0 . Тогда решение уравнения (5) имеет вид
	y(x) =C ex λ−2	+C	e−x λ−2 .
	1	2

Удовлетворим граничным условиям:

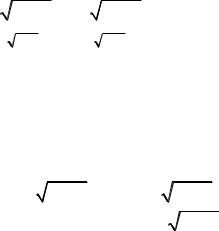
C λ −2 −C				2	λ −2 = 0;
	1			2
			e− λ−2 = 0.
C e λ−2 +C			e− λ−2 = 0.
	1	2
Отсюда следует, что C1 =C2 = 0 ,		то есть y(x) ≡ 0 , что противоречит
определению собственной функции.

2)	λ −2 = 0 . Решение уравнения (5) в этом случае имеет вид y(x) =C1 +C2 x , и
краевым условиям удовлетворяет только нулевая функция.
3)	λ −2 < 0 . Решение уравнения (5) имеет вид

y(x) =C1 cos x 2 −λ +C2 sin x							2 −λ .
Подставляя краевые условия, получим C2 = 0 и cos							2 −λ = 0 . Находим спектр
		π2	(2n +1)2
λ	= 2 −					, n .
λ	= 2 −					, n .
n			4
Соответствующие собственные функции (принадлежащие L2 [0,1]) имеют вид
yn (x)=C cos				π (2n +1)x			.
yn (x)=C cos							.
					2
VI. Проверить, является	ли оператор				двукратного			дифференцирования
(Ay = y′′), определенный в	комплексном				пространстве			L (a,b) на дважды
								2

непрерывно дифференцируемых функциях u , удовлетворяющих граничным условиям u′(a)=u (a), u (b)= 0 , симметричным. Каким граничным условиям

удовлетворяют функции из области определения сопряженного оператора?

Решение. Оператор A называется симметричным, если выполняется условие

u,v D(A): (Au,v)=(u, Av).

(6)

Возьмем u (t ),v(t ) D(A) L2 [a,b]. Тогда

′′

′

′ ′

′

′′

′

(Au,v)= ∫

u vdt =u v

− ∫

u v dt =(u v −uv )

+ ∫

uv dt =(u v

−uv )

+(u, Av).

A необходимо и достаточно

Следовательно,

для симметричности оператора

выполнения условия

′

то есть

(u v −uv )

a = 0 ,

u′(b)v (b)−u (b)v′(b)−u′(a)v (a)+u (a)v′(a)= 0 .

(7)

Так

как

u,v D(A), то

функции

u,v

удовлетворяют

заданным

граничным условиям. Подставим их в (7):

u′(b) 0 −0 v′(b)−u (a)v (a)+u (a)v (a)= 0 .

Полученное верное равенство равносильно симметричности оператора A .

Пусть A

- оператор, сопряженный с A . Он определяется так. v D(A ),

если существует элемент (обозначим его

A* v )

такой,

что

(сравните с

условием (6)):

u D(A): (Au,v)=(u, A v).

Это условие аналогично условию (7), но u D(A), а v D(A ). Подставим в

(6) условия на функцию u :

u′(b)v (b)+u (a)(v′(a)−v (a))= 0 .

Поскольку u′(b) и u (a) произвольны, получаем граничные условия на функцию v D(A ): v′(a)= v(a), v(b)= 0 , откуда следует, что граничные

условия для элемента из области определения A* те же, что и для оператора

A .

Задачи для самостоятельного решения

I. Проверить, образует ли (

X , ρ)

метрическое пространство.

[

]

(

)

t [a,b]

′

X =C

a,b , ρ

x, y

= max

x (t) − y (t)

;

X =C[0,1],

ρ(x, y)=

x(1 2)− y (1 2)

;

X =

{

}

(

x, y

)

arg x −arg y

=1 ,

;

X =C, ρ(x

, y)=

Re x Re y −Im x Im y

;

X =C2 , ρ(x, y)= max

Re x −Re y

;

i=1,2

X =C, ρ(x, y)=

Re x −Re y

Im x −Im y

;

X = Rn , ρ(x, y)= max

− y2

;

1≤i≤n

X =l∞,

x =(x1, x2 ,K, xn ,K),

ρ(x, y)=sup

xn − yn

;

∞

X =l1, x =(x1, x2 ,K, xn ,K), ρ(x, y)

= ∑

xi − yi

;

i=1

10. X = Mm×n - матрицы размером m ×n , ρ(x, y)= max (xij − yij );

i, j

11. X =

x =(x , x , x

)

, ρ(x, y)=

− y

;

3 , ρ(x, y) - длина хорды,

12. X - сфера в трехмерном пространстве

соединяющей точки x, y ;

13. X - сфера в трехмерном пространстве

3 , ρ(x, y) - длина кратчайшей

дуги большого круга, проходящего через точки x, y ;

14.

X =C[a,b],

ρ(x, y)

= ∫b

x(t) y(t)

dt ;

15.

X =C[a,b],

ρ(x, y)

= ∫b

x(t) + y(t)

dt ;

[

]

(

)

t [a,b]

16.

X =C

a,b

x, y

= max

x(t)

−

y(t)

;

17.

X = L1 (a,b),

ρ(x, y)= ∫ab

x(t) − y(t)

dt ;

[

]

(

)

t [a,b]

18.

X =C

a,b

x, y

= max

x(t) − y(t)

;

19.X = , ρ(x, y)= x − y ;

20.X = , ρ(x, y)= x − y .

II. Проверить, можно ли ввести норму указанным образом.

∞

1.X =l1, x =(x1, x2 ,K, xn ,K), x = ∑ xi ;

x =(x1, x2 ,K, xn ,K),

i=1

X =l∞,

=sup

;

X = n ,

∑xi

;

i=1

X =

n ,

= max

−min

;

X =

n ,

x − x

;

= max

X =

n ,

x − x

= max

;

X =

n ,

x =(ξ ,K,ξ

= max

ξ ξ

;

i,k

X =C[a,b],

∫b x(t )dt

;

X =C[a,b],

= ∫b

x(t )

dt ;

[

]

(

)

t [a,b]

10.

X =C

a,b

max x

;

X =C1 [a,b],

11.

= max

x′(t )

;

12.

[

]

t [a,b]

( )

′

( )

t [a,b]

X =C

a,b ,

= max

x t

+ x

;

13.

X =C1 [a,b],

= max

x′(t )

+ max

(t )

;

t [a,b]

14.

X =C2 [a,b],

= tmax[a,b](

x′(t )

x′′(t )

)

15.

X =C

a,b

= max

′′

+ max

′

+ max

;

[

]

t [a,b]

(

)

t [a,b]

(

)

t [a,b]

(

)

16.X =C1 [a,b], x = ∫ab x′(t )dt ;

17.

[ ]

t [a,b] ( )

′

( )

X =C

a,b ,

= max

x t x

;

∫b

18.

X =C1

[a,b],

x′(t )

2 dt ;

19.

X =C

[a,b],

∫

′

(t )

dt ;

x(t )x

20.

X =C

[a,b],

∫

′

dt .

x(t )+ x

(t )

III. В пространстве Η найти проекцию элемента x на подпространство, порожденное f1, f2 ,K, fn .

1.	Η = L	(−π,π ),		x =t2 ,		f			=1,					f		2		=sin 2t,															f	3	= cos 2t ;
	2	(0,2π ),				1										2																		3
2.	Η = L2	(0,2π ),		x =t +1,			f1 =sin t,															f2 = cost ;
3.	Η = L2	(0,2π ),		x = cost,					f1 =1,									f2 = 2sin t ;
4.	Η = L	(−π,π ),		x = cos2 t,						f			=1,							f		2		= cost,											f	3	=sin 2t ;
	2	(0,2π ),									1											2														3
5.	Η = L	(0,2π ),		x = et ,	f			= cost,											f		2		=sin t ;
	2	(0,π ),				1															2
6.	Η = L	(0,π ),	x =sin t,			f			=1,						f		2		=t,							f	3				=t2				;
	2	(−1,1),				1											2										3
7.	Η = L	(−1,1),		x = 3 t ,	f		=1,						f	2				=t,						f	3			=t2 ;
	2	(0,1),				1								2											3
8.	Η = L	(0,1),	x = t , f			=t,					f	2			=t2 ;
	2	(−1,1),		1								2
9.	Η = L	(−1,1),		x = e2t ,	f			=1,					f		2			=t ;
	2	(−1,1),				1									2
10.	Η = L	(−1,1),		x = cost,		f				=1,							f	2		=t,							f		3			=t2 ;
	2	(−2,2),						1										2											3
11.	Η = L	(−2,2),		x = et+1,		f				=1,						f		2		=t, f								3			=t2				;
	2	(−2,2),					1											2										3
12.	Η = L	(−2,2),		x =tet ,		f			=1,				f			2		=t ;
	2	(−1,1),				1										2
13.	Η = L	(−1,1),		x =te−t ,		f			=1,						f		2		=t2 ;
	2	(−π,π ),				1											2
14.	Η = L	(−π,π ),		x = cost,					f		=1,							f		2		=t,								f		3	=t3 ;
	2	(−1,1),								1										2												3
15.	Η = L	(−1,1),		x = e2t ,	f			=1,					f		2			=t,						f		3			=t3 ;
	2	(0,π ),				1									2											3
16.	Η = L2	(0,π ),	x =t, f1 =1,							f2 sin 2t ;
17.	Η = L	(−1,1),		x =t3, f		=1,					f		2			=t,							f	3		=t3 +t ;
	2	(−1,1),		1									2											3
18.	Η = L	(−1,1),		x =sin2 t,					f		=1,							f	2			=t,							f		3		=t2 ;
	2								1										2												3

19.	Η = L2 (−π,π ),		x = 2t +1,	f1 =sin t,			f2 = cos 2t ;
20.	Η = L	(−π,π ),	x =t2 −1,	f	=1, f	2	=sin 2t .
	2			1		2

IV. Показать, что оператор A ограничен в пространстве X , и найти его норму.

1.(Af )(s)

2.(Af )(s)

3.(Af )(s)

4.(Af )(s)

5.(Af )(s)

6.(Af )(s)

7.(Af )(s)

8.(Af )(s)

9.(Af )(s)

10.(Af )(s)

11.(Af )(s)

12.(Af )(s)

13.(Af )(s)

14.(Af )(s)

15.(Af )(s)

16.(Af )(s)

17.(Af )(s)

18.(Af )(s)

19.(Af )(s)

20.(Af )(s)

= ∫0π 2 ssin t f (t )dt,

X =C[0,π 2];

= ∫1(s2

+t2 )f (t )dt,

X =C[0,1];

= ∫1 s2t2 f (t )dt,

X =C[0,1];

f (t )dt,

X =C[0,π];

∫0

+sin

(

+t3

)

(

)

dt,

X =C

0,1 ;

∫

[ ]

(st + s2t2 )f (t )dt, X =C[0,2];

= ∫2

= ∫1(s +t )tf (t )dt,

X =C[0,1];

1et+s f

(

)

dt,

X =C

[

0,1

;

∫0

]

= ∫1 set

f (t )dt,

X =C[0,1];

= ∫1et+stf (t )dt,

X =C[0,1];

= ∫0π 2 s2 sin t

f (t )dt,

X =C[0,π 2];

= ∫π 2 (s +sin2 t )f (t )dt,

X =C[0,π 2];

+ 2)t2 f (t )dt,

= ∫1(s2

X =C[0,1];

(s3

+t3 )tf (t )dt,

= ∫2

X =C[0,2];

+ s3t )f (t )dt,

= ∫1(s2

X =C[0,1];

= ∫1(s + s3t )f (t )dt,

X =C[0,1];

= ∫02 2s+3t

f (t )dt, X =C[0,2];

= ∫1 s3t

f (t )dt,

X =C[0,1];

= ∫2 es 2t+1 f (t )dt,

X =C[0,2];

1es sin t

(

)

dt,

X =C

[

0,1 .

∫0

]

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.09.2019300.54 Кб2Философия (элементарный курс).doc
#
11.09.2019144.54 Кб2ФИЛОСОФИЯ - ЭКЗАМЕН.docx
#
20.03.201683.13 Кб12философия ответы.docx
#
25.11.2019317.44 Кб16Фотометрия и колориметрия.doc
#
22.09.2019112.13 Кб5ФРАЗЕОЛОГИЧЕСКИЕ СРЕДСТВА.doc
#
21.03.2016351.04 Кб28Функан расчет.pdf
#
16.09.2019701.44 Кб4хахаев.doc
#
25.08.2019375.3 Кб2хоз право.doc
#
20.03.2016350.26 Кб52Хрестоматия по Философии Часть 3Word.docx
#
20.03.2016453.72 Кб69ХС.docx
#
21.03.20161.87 Mб475Цифровая обработка сигналов.pdf