Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Функан расчет

.pdf

Скачиваний:

Добавлен:

21.03.2016

Размер:

351.04 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

V. Найти точечный спектр и собственные функции оператора A в L2 [a,b].

1.Ay =π2 y′′+ 94 y, y (0)= y (3π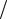2)= 0 ;

2.	Ay =π2 (1 − y′′), y′(0)= y (π )= 0 ;
3.	Ay = 4(y′′+9 y), y′(0)= y′(1)= 0 ;
4.	Ay = −4 y′′+9 y, y(0)= y(π )= 0 ;

5.Ay =π2 y − y′′, y(0)= y(π )= 0 ;

6.Ay = 2 y′′+3y, y′(0)= y(π )= 0 ;

7.Ay = −y′′+ 4 y, y (0)= y′(π2)= 0;

8.Ay = y′′+ 4 y, y′(0)= y′(π2)= 0 ;

9.Ay =9 y′′+ 4 y, y′(0)= y′(1)= 0 ;

10.Ay =16 y − y′′, y(0)= y′(4)= 0 ;

11.Ay = −9 y′′− y, y (0)= y (1)= 0 ;

12.Ay = −4 y′′+ y, y(0)= y(2)= 0 ;

13.Ay = −y′′− y, y (−π )= y (π )= 0 ;

14.Ay = y′′−6 y, y (0)= y (2)= 0 ;

15.Ay =9 y − y′′, y′(0)= y (π2)= 0 ;

16.Ay = y − y′′, y (0)= y′(1)= 0 ;

17.Ay = y′′+ y, y′(0)= y′(1)= 0 ;

18.Ay = y′′, y′(0)= y′(1)= 0 ;

19.Ay = y′′+ 4 y, y (0)= y (π )= 0 ;

20.Ay = y′′, y(0)= y(1)= 0 .

VI. Проверить, является ли оператор двукратного дифференцирования (Ay = y′′), определенный в комплексном пространстве L2 (a,b) на дважды

непрерывно дифференцируемых функциях, удовлетворяющих указанным граничным условиям, симметричным. Каким граничным условиям удовлетворяют функции из области определения сопряженного оператора?

1.u′(a)=u′(b)= 0 ;

2.u′(a)−2u (a)= 0, u (b)= 0 ;

3.u (a)=u (b)= 0 ;

4.u′(a)=u (a), u′(b)=u (b);

5.u′(a)−2iu (a)= 0, u (b)= 0 ;

u (a)= 0, u′(b)=(1 +i)u (b);

u′(a)= 0, u′(b)+10u (b)= 0 ;

5iu′(a)+u (a)= 0, u′(b)= 0 ;

′

1 +i

(a)+1 −i u

(a)= 0, u (b)= 0 ;

10.

3iu′(a)−u (a)= 0, u (b)= 0 ;

11.

u′(a)=u (b)= 0 ;

12.

u′(a)= 2u (a), u′(b)=iu (b);

13.

u′(a)=u (a), u′(b)= 0 ;

i +

′

14.

(a)+1 +i u

(a)= 0, u (b)= 0 ;

′

u (a)

′

15.

(a)− 2i +3

= 0, u

(b)=u (b);

16.

2iu′(a)+(4 +i)u (a)= 0, u (b)= 0 ;

17.

(i +1)u′(a)−(2i −1)u (a)= 0, u (b)= 0 ;

18.

u′(a)

=u (a),

u′(b)

=u (b);

2i +3

i +1

19.2u′

20.u′(a)= ui +(a4), u′(b)= 2iu (b).(a)=u (a), u′(b)= 2u (b);

Типовой расчет № 2 «Интегральные уравнения»

I. Для заданного ядра K (s,t ) интегрального оператора, заданного на отрезке

[a,b]

1)построить резольвенту Фредгольма тремя способами: а) с помощью ряда Неймана; б) с помощью рядов Фредгольма; в) как для вырожденного ядра.

2)найти характеристические значения и собственные функции двумя способами:

а) как для вырожденного ядра; б) через особенности резольвенты Фредгольма.

1)Пусть K (s,t )= s −t , a = 0 , b =1.

Речь идет о решении интегрального уравнения
f − Mf = h ,	(1)
где M - интегральный оператор с ядром K (s,t ):
(Mf )(s)= λ∫b K (s,t ) f (t )dt ,	(2)
a

h - заданная функция.

а) Решение уравнения (1) будем искать методом последовательных приближений. Для этого полагаем

∞
f (s)= h(s)+ ∑ϕn (s)λn ,
n=1
где функции ϕn задаются формулами:
ϕ1 (s)= ∫ab K (s,t ) f (t )dt ,
ϕn (s)= ∫ab K (s,t )ϕn−1 (t )dt = ∫ab Kn (s,t ) f (t )dt для n ≥ 2 ,
где Kn (s,t ) называется итерированным ядром и определяется как
Kn (s,t )= ∫ab dt1 ∫ab dt2 K∫ab K (s,t1 )K (t1,t2 )KK (tn−1,t )dtn−1, n ≥ 2 ,	(3)
K1 (s,t )≡ K (s,t ).

Тогда решение уравнения (1) может быть найдено в виде f = h +λRh , где R -

интегральный оператор с ядром R(s,t;λ), называемым	резольвентой
Фредгольма. Для резольвенты Фредгольма справедливо равенство
∞
R(s,t;λ)= ∑Kn (s,t )λn−1 ,	(4)

n=1

где ряд, стоящий справа, называется рядом Неймана.

Найдем последовательно итерированные ядра, следуя формуле (3). Имеем

													K1 (s,t )= s −t ,							1 (s +t )− st −						1
		K (s,t )			=		1 K (s,t				)K (t		,t )dt =		1(s −t )(t −t )dt =					1 (s +t )− st −						1	,
		2					∫0			1	1			1	∫0	1	1		1	2						3
		2								1	1			1		1	1		1
K	3	(s,t )= 1 K (s,t						)K		2	(t ,t )dt = 1(s −t					) 1 (t +t )			−t t − 1 dt = −					1	(s −t ),
K		(s,t )= 1 K (s,t						)K			(t ,t )dt = 1(s −t					) 1 (t +t )			−t t − 1 dt = −						(s −t ),
			∫0				1				1		1	∫0	1		1		1			1	12
			∫0											∫0		2					3		12
			K			(s,t )= −			1			1(s	−t	)(t	−t )dt = −		1 1		(s +t )− st −				1 ,
			K	4		(s,t )= −						1(s	−t	)(t	−t )dt = −				(s +t )− st −				1 ,
								12 ∫0									12 2						3
			K	5		(s,t )= −				1		1(s −t		) 1	(t +t )−t t − 1 dt =						1	(s −t ).
			K			(s,t )= −						1(s −t		) 1	(t +t )−t t − 1 dt =							(s −t ).
								12 ∫0					1		1	1			1	122
								12 ∫0						2				3		122

Методом математической индукции можно доказать, что итерированные ядра имеют вид:

K2m−1 (s,t )=		(−1)m−1				(s −t ),
		12m−1

K2m (s,t )=	(−1)m−1		1	(s	+t )− st −		1	,
	12m−1		2				3

где m =1,2,3,K.
Тогда ряд Неймана для резольвенты примет вид
				∞		(−1)n−1				1	(s +t )− st −			1	∞			(−1)m−1
R(s,t;λ)=(s −t )∑						12	n−1 λ2n−2 +				(s +t )− st −			3	∑			12	m−1 λ2n−1		=
			n=1			12				2				3	n=1			12
													s −t +λ			1	(s +t )− st −			1
	1			1				1		λ			s −t +λ				(s +t )− st −
=(s −t )	1			1	(s +t )− st −			1		λ					2					3		.
			+									=			2					3
		λ2	+	2				3			λ2	=						λ2
	1 +	λ2		2				3	1 +		λ2					1 +		λ2
	1 +	12							1 +		12					1 +		12
		12									12							12

б) Резольвента Фредгольма уравнения (1) может быть найдена по формуле:

R(s,t;λ)= D(s(,t;)λ),

D λ

где функции D(s,t;λ) и D(λ) находятся с помощью рядов Фредгольма:

			∞	(−1)		n
		D(λ)=1 + ∑		(−1)		dnλn ,
			n=1	n!			K K (t1,tn )
			K (t1,t1 )		K (t1,t2 )
			K (t1,t1 )		K (t1,t2 )
b	b	b	K (t2 ,t1 )		K (t2 ,t2 )		K K (t2 ,tn )
dn = ∫a dt1	∫a dt2 K∫a dtn		M					,
			K (tn ,t1 )		K (tn ,t2 )		K K (tn ,tn )

			∞	(−1)		n
D(s,t;λ)= K (s,t )+ ∑				(−1)		dn (s,t )λn ,
			n=1	n!
			K (s,t )			K (s,t1 )	K K (s,tn )
			K (s,t )			K (s,t1 )	K K (s,tn )
b	b	b	K (t1,t )		K (t1,t1 )		K K (t1,tn )
dn (s,t )= ∫a dt1	∫a dt2 K∫a dtn		M					.
			K (tn ,t )		K (tn ,t1 )		K K (tn ,tn )

Имеем

		d1 = ∫ab K (t1,t1 )dt1 = ∫01(t1 −t1 )dt1 = 0 ,
b b	K (t ,t )		K (t ,t					)	dt1dt2			1 1		0	t −t	2	dt1dt2	= 6 ,
b b	K (t ,t )		K (t ,t					)				1 1		0	t −t
d2 = ∫∫	K (t ,t )		K	(t ,t				)				= ∫∫	t −t		0
	1	1			1		2								1			1
a a	2	1			2		2					0 0	2	1
a a	2	1			2		2					0 0	2	1
		1 1 1		0				t1 −t2				t1 −t3
		1 1 1		0				t1 −t2				t1 −t3
	d3 = ∫∫∫		t2 −t1							0		t2 −t3		dt1dt2dt3 = 0,
		0 0 0	t	−t				t	3	−t	2	0
			3			1			3		2

так как подынтегральный определитель равен нулю. Очевидно, что dn = 0 при n ≥3. Следовательно,

D(λ)=1 +121 λ2 .

Далее,

b	K (s,t )	K (s,t	)		1	s −t s −t			1		1

d1 (s,t )= ∫	K (t ,t )	1	)	dt1	= ∫		1	dt1 =		+ts −		(s +t ),
		K (t ,t				t −t	0		3		2
a	1	1 1			0	1

1 1

d2 (s,t )= ∫∫

0 0

s −t	s −t1	s −t2
s −t	s −t1	s −t2
t1 −t	0	t1 −t2	dt1dt2 = 0,
t2 −t	t2 −t1	0

так как подынтегральный определитель равен нулю. Очевидно, что dn (s,t )= 0 при n ≥ 2 . Следовательно,

	1	(s +t )− st −	1
D(s,t;λ)= s −t +λ	2	(s +t )− st −	3	.
	2		3

Окончательно, получаем резольвенту

		1	(s +t )− st		−	1
	s −t +λ	2	(s +t )− st		−	3
R(s,t;λ)=		2				3		.
R(s,t;λ)=		1 +		λ2				.
				λ2
				12
				12
в) Перепишем уравнение (1) в виде
f (s)= h(s)+λ∫1(s −t ) f (t )dt = h(s)+λs∫1 f (t )dt −λ∫1t f (t )dt .
0				0			0
Введем обозначения
c1 = ∫01 f (t )dt , c2 = ∫01t f (t )dt .							(5)
Тогда уравнение (1) равносильно равенству
f (s)= h(s)+λsc1 −λc2 .							(6)

Подставим выражение (6) в равенства (5). Получим систему уравнений для c1 и c2 :

1 −

1 λ c

λc

= 1h(t )dt;

∫0

1 λc

1 +

1 λ

1t h(t )dt.

−

∫0

Решение этой системы имеет вид

1 + 1

∫01h(t )dt −

∫01t h(t )dt ,

c1 =

1 +

λ2

1 +

λ2

1 − 1

1 λ

1h(t )dt .

h(t )dt +

1 +

λ2 ∫0

1 +

λ2

∫0

Далее, записывая решение (6) уравнения (1), получаем резольвенту Фредгольма

	1 +		1														1						1
	1 +		2		λ			λt						1	−		2	λ			t		3		λ
R(s,t;λ)= s			2				−	λt					−				2					+	3					=
R(s,t;λ)= s			1				−	1					−				1					+		1				=
	1 +		1		λ	2	1 +	1		λ	2			1 +			1		λ		2	1 +		1		λ	2
	1 +	12			λ		1 +	12		λ				1 +		12			λ			1 +	12			λ
		12						12								12							12
								1	(s		+t )− st −						1
				s −t +λ				2	(s		+t )− st −						3
		=						2									3			.
		=						1 +			λ2									.
											λ2
											12
											12
2) Пусть K (s,t )=1 +3st , a = 0 , b =1.
а) Запишем однородное уравнение Фредгольма в виде
f (s)= λ∫1(1 +3st ) f (t )dt = λ∫1 f (t )dt +3λs∫1t f																								(t )dt .
0												0										0

Вводя обозначения

c1 = ∫01 f (t )dt , c2 = ∫01t f (t )dt ,

получим

f (s)= λc1 +λc2s .

Тогда для c1 и c2 имеем систему уравнений:

(λ −1)c +			3	λc = 0;
		1	2	2
	1 λc +(λ			(7)
	1 λc +(λ		−1)c = 0.
	2	1		2
	2

Из условия существования нетривиального решения

λ −1		3	λ
1		2		= 0
1	λ	λ −1
2

находим характеристические значения λ1,2 = 4 ± 2 3 .

Так как из	(7) следует, что c2	= −		λc1		, то подставляя λ1,2 , получаем
Так как из	(7) следует, что c2	= −	2	(λ −	1)	, то подставляя λ1,2 , получаем
			2	(λ −	1)
выражения для собственных функций:
	f1,2 (s)=(4 ± 2	3 )c1 (1 m s			3 )= c(1 m s 3),
где c =(4 ± 2	3)c1 .

б) Известно, что характеристические числа интегрального уравнения являются полюсами резольвенты R(s,t;λ) (как функции от λ ), а ее коэффициенты рядов

Лорана (в выколотых окрестностях этих полюсов) при наибольшей по модулю отрицательной степени дают соответствующие этим значениям собственные функции (как функции от первого аргумента при любом значении t ).

Пусть для ядра K (s,t )=1 +3st , a = 0 , b =1 резольвента уже найдена:

1 +3st +λ

(s +t )−3st −1

R(s,t;λ)=

1 λ2

−2λ +1

Числа λ1,2 = 4 ± 2

3 - ее простые полюса. Имеем для собственной функции

1 +3st +λ

(s +t )

−3st −1

(s)=

res

R(s,t;λ)=

λ=4+2 3

−2λ

dλ

λ=4+2 3

=(2 + 3)(t 3 −1)(1 − s 3 )= c(1 − s 3),

где c =(2 +

3 )(t

3 −1).

Аналогично находится

f2 (s)= c(1 + s

3).

II. Решить уравнение или систему уравнений.

ϕ′′(x)+ ∫e2(x−t)ϕ′(t )dt = e2x , ϕ(0)= 0, ϕ′(0)=1.

Применим преобразование Лапласа к левой и правой частям. Обозначим образ функции ϕ(x)↔ Φ(p). Имеем для правой части e2x ↔ p 1−2 .

В силу правила дифференцирования оригинала и учитывая данные начальные условия, получим

ϕ′(x)↔ pΦ(p)−ϕ(0)= pΦ(p),

ϕ′′(x)↔ p2Φ(p)− pϕ(0)−ϕ′(0)= p2Φ(p)−1.

Пользуясь свойством умножения изображений, получим

∫x e2(x−t )ϕ′(t )dt ↔ p p−2 Φ(p).

Тогда уравнение для образа искомой функции примет вид

p2Φ(p)−1 +

Φ(p)=

p −2

Решая его,

получим

Φ(p)=

−

. Следовательно, решение

p(p −1)

p −1

исходного

уравнения

с данными

начальными условиями имеет вид

ϕ(x)= ex −1.

Задачи для самостоятельного решения

I. Для заданного ядра K (s,t ) интегрального оператора, заданного на отрезке

[a,b]

2)найти характеристические значения и собственные функции двумя способами:

а) как для вырожденного ядра; б) через особенности резольвенты Фредгольма.

1.K (s,t )= st2 + s2t, a = 0, b =1;

2.K (s,t )= es +et , a = 0, b =1;

3.K (s,t )=sin2 (s −t ), a = 0, b = 2π ;

4.K (s,t )= st + 2s2t2 , a = −1, b =1;

5.K (s,t )=sin ssin t +cos 2s cos 2t, a = −π, b =π ;

6.K (s,t )= s3t3 + s2t2 , a = −1, b =1;

7.K (s,t )= st (s +t ), a = −1, b =1;

8.K (s,t )=t2 + s2 , a = 0, b =1;

9.K (s,t )= cos(s −t ), a = 0, b =π ;

10.K (s,t )= es+t (s +t ), a = 0, b =1;

11.K (s,t )= s2t2 (1+ s2t2 ), a = 0, b =1;

12.K (s,t )=sin (s +t ), a = 0, b = 2π ;

13.K (s,t )= es+t (s +t ), a = −1, b = 0 ;

14.K (s,t )= e−s +e−t , a = 0, b =1;

15.K (s,t )= s2 +t2 , a = −1, b =1;

16.K (s,t )= st2 + s2t, a = −1, b =1;

17.K (s,t )= st3 + s3t, a = −1, b =1;

18.K (s,t )= 2st +3s2t2 , a = −2, b = 2 ;

19.K (s,t )= st +cos s cost, a = −π, b =π ;

20.K (s,t )=3st +5s2t2 , a = −1, b =1.

II. Решить уравнение или систему уравнений:

1. ϕ(x)=1 + x + ∫e−2(x−t )ϕ(t )dt ;

2.ϕ(x)= x + ∫sin (x −t )ϕ(t )dt ;

3.ϕ(x)=sin x + ∫(x −t )ϕ(t )dt ;

4.ϕ(x)= x − ∫sh (x −t )ϕ(t )dt ;

5.ϕ(x)=1 −2x −4x2 + ∫x (3 +6(x −t )+ 4(x −t )2 )ϕ(t )dt ;

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.09.2019300.54 Кб2Философия (элементарный курс).doc
#
11.09.2019144.54 Кб2ФИЛОСОФИЯ - ЭКЗАМЕН.docx
#
20.03.201683.13 Кб12философия ответы.docx
#
25.11.2019317.44 Кб16Фотометрия и колориметрия.doc
#
22.09.2019112.13 Кб5ФРАЗЕОЛОГИЧЕСКИЕ СРЕДСТВА.doc
#
21.03.2016351.04 Кб28Функан расчет.pdf
#
16.09.2019701.44 Кб4хахаев.doc
#
25.08.2019375.3 Кб2хоз право.doc
#
20.03.2016350.26 Кб52Хрестоматия по Философии Часть 3Word.docx
#
20.03.2016453.72 Кб69ХС.docx
#
21.03.20161.87 Mб476Цифровая обработка сигналов.pdf