САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ

ИНСТИТУТ ТОЧНОЙ МЕХАНИКИ И ОПТИКИ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

 

Кафедра электротехники и прецизионных

электромеханических систем

 

Ю.М. Осипов

 

ЧАСТОТНЫЙ И ВРЕМЕННОЙ АНАЛИЗ

СТАЦИОНАРНЫХ И ПЕРЕХОДНЫХ ХАРАКТЕРИСТИК ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

 

Учебное пособие по курсам электротехники и ТОЭ

Часть вторая

 

Санкт-Петербург

2002

УДК

Осипов Ю.М. Частотный и временной анализ стационарных и переходных характеристик линейных электрических цепей. Учебное пособие по курсам электротехники и ТОЭ. Ч. 2. – СПб: СПбГИТМО (ТУ), 2002 – 99 с.

Рецензент: Проф., докт. Техн. Наук, зав. Каф. ТОЭ СПбГЭТУ(ЛЭТИ) Бычков Ю. А.

Рекомендовано кафедрой электротехники и прецизионных электромеханических систем СПбГИТМО,

 

© Санкт- Петербургский государственный институт точной механики и оптики (Технический Университет), 2002

 

В авторской редакции

Компьютерная верстка и дизайн В.И. Евлентьева

О.А. Яковлева

Зав. редакционно-издательским отделом Н.Ф. Гусарова

Отпечатано на ризографе. Тираж 100 экз. Заказ № 93

СОДЕРЖАНИЕ

 1. Частотные характеристики. Резонансные явления

 1.1. Частотные характеристики двухполюсников

1.2. Частотные характеристики реактивных двухполюсников

1.3. Резонансные режимы двухполюсников с потерями

1.4. Частотные характеристики четырехполюсников

1.5. Определение внешних частотных характеристик через А-параметры

 2. Частотный анализ цепей при действии несинусоидальных периодических сигналов

 2.1. Спектры периодических сигналов

2.2. Определение реакции линейной цепи на действие негармонического периодического сигнала

 3. Переходные процессы в линейных электрических цепях

 3.1. Основные определения и физические условия

3.2. Электрические цепи первого порядка

3.3. Переходные процессы в цепях второго порядка

3.4. Уравнения состояния электрической цепи

3.4.1. Использование законов Кирхгофа

3.4.2. Использование метода наложения

3.4.3. Решение уравнений состояния цепи

3.5. Расчет переходных процессов операторным методом

4. Задачи для самостоятельного решения

 Приложение 1. Задачи к первому разделу пособия

Приложение 2. Задачи ко второму разделу пособия

Приложение 3. Задачи к третьему разделу пособия

Приложение 4. Решение уравнений состояния электрической сети

 История развития электротехнического образования в Институте Точной Механики и Оптики

 Список литературы

1. Частотные характеристики. Резонансные явления

1.1 Частотные характеристики двухполюсников

 

Пассивные двухполюсники и четырехполюсники включают набор резистивных и реактивных (индуктивных и емкостных) элементов, в которых протекают электрические токи под действием какого-либо одного внешнего источника энергии. Для описания физических явлений в таких цепях при воздействии на входных зажимах источника гармонических колебаний с фиксированной частотой =const используют метод комплексных амплитуд, который в свою очередь основывается на введении понятий комплексных сопротивлений или проводимостей отдельных элементов цепи -r, , , а также комплексных амплитуд токов и напряжений – , [1].

В общем случае у источника гармонических колебаний может изменяться не только амплитуда и начальная фаза, но и угловая частота - . Тогда комплексная характеристика источника (входного воздействия) записывается в виде функции мнимой комплексной переменной - ( ). Эту характеристику обычно записывают в показательной (полярной) форме и называют комплексной спектральной плотностью. Модуль этой характеристики называют спектральной плотностью, а аргумент - фазовой плотностью или фазочастотной характеристикой. Так для напряжения имеем:

где - спектральная плотность напряжения, - фазовая плотность напряжения.

Аналогично гармонический ток с переменной угловой частотой ω характеризуется своей комплексной спектральной плотностью:

В зависимости от вида входного воздействия (электрического сигнала) спектральные плотности могут иметь непрерывный или дискретный характер. В дальнейшем для краткости будем опускать написание зависимости от угловой частоты, полагая , , , .

В реальном двухполюснике или четырехполюснике комплексные плотности токов и напряжений связаны между собой соотношениями, зависящими как от внутренних свойств элементов цепи, так и от способа соединения ветвей. Подобного рода соотношения называются частотными характеристиками.

 

На рис.1.1а изображен двухполюсник, имеющий два входных зажима, к которым подсоединяется источник входного сигнала. Если к цепи присоединяется источник тока J(t), то входной ток i(t) = J(t), т.е. будет независимой функцией времени, а напряжение u(t) на входе определится через свойства цепи как зависимая функция. При гармоническом характере входного сигнала определяют отношение комплексов напряжения и тока.

(1.1)

Такое отношение называют комплексным входным сопротивлением

двухполюсника:

Из определения (1.1) следует, что Z(jω) в свою очередь включает две характеристики: - амплитудно-частотную характеристику (АЧХ) и - фазочастотную характеристику (ФЧХ) функции входного сопротивления.

а) б)

Рис. 1.1. Обобщенная комплексная схема замещения цепи:

а) двухполюсника; б) четырехполюсника

 

Если к цепи присоединяется источник напряжения e(t), то напряжение на двухполюснике u(t) = e(t), т.е. будет независимой функцией времени, a ток i(t) определится через свойства цепи как зависимая функция. При гармоническом характере входного сигнала определяют отношение тока к напряжению, которое называют комплексной входной проводимостью двухполюсника:

где Y(ω) и φ(ω) называют соответственно АЧХ и ФЧХ функции входной проводимости.

Функции Z(jω) и Y(jω) являются взаимно обратными функциями. В определении этих функций входят токи и напряжения, что дает возможность находить эти характеристики опытным путем, используя вольтметр, амперметр и прибор, измеряющий фазу гармонического колебания. Однако сами функции в силу линейности рассматриваемых цепей не зависят от величин токов и напряжений и могут быть определены непосредственно по структуре (топологии) цепи с учетом характера элементной базы ветвей. Для нахождения этих характеристик могут быть использованы все известные методы расчета цепей постоянного тока: законы Кирхгофа, простейшие преобразования, упрощающие схему и т.п. [1]. Исследование этих характеристик позволяет предсказать поведение цепи при различного рода воздействиях, о чем будет сказано далее.

 

Пример 1.1. Найти АЧХ и ФЧХ для функции входного сопротивления двухполюсника, образованного параллельным соединением резистивного и индуктивного элемента (рис.1.2а). Питание цепи осуществляется от источника синусоидального тока с любой частотой.

а) б)

Рис. 1.2. Схема для исследования входного сопротивления двухполюсника:

а) исходная схема; б) комплексная схема замещения

 

Решение задачи начинаем с построения комплексной схемы замещения исходной цепи (рис. 1.2б), на входе которой действует комплексный спектр источника тока I(jω) = J(jω), в результате чего на двухполюснике будет иметь место комплексный спектр напряжения U(jω). Отношение их, определяемое выражением (1.1), может быть найдено непосредственно по структуре цепи путем объединения комплексных сопротивлений параллельно соединенных ветвей:

 

Сравнивая модули и аргументы, запишем АЧХ и ФЧХ

- АЧХ функции входного сопротивленияисследуемого выражения

φ(ω) = - ФЧХ функции входного сопротивления.

При построении графиков целесообразно перейти к относительной переменной Ω = ωL/r, которая указывает во сколько раз сопротивление индуктивности на данной частоте больше резистивного сопротивления. Для

этой переменной полученные выше выражения перепишутся в виде

Графики найденных функций представлены на рис.1.3а и рис.1.3б в относительных масштабных единицах.

 

а) б)

Рис. 1.3. Частотные характеристики функции входного сопротивления: а)АЧХ; б)ФЧХ

 

Расчетные значения сведены в таблице 1.

Таблица 1

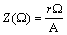		, Ом	, градусы	, градусы
0	1.0	0	0	90
0.5	1.12	0.447r	26.5	63.5
1.0	1.41	0.707r	45.0	45.0
1.5	1.80	0.832r	56.3	33.7
2.0	2.23	0.894r	63.4	26.6
2.5	2.69	0.928r	68.2	21.8
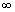
		r	90	0

 

Для перехода к реальной частоте необходимо знать численные значения параметров цепи r и L .Тогда переход осуществляется по формуле ω = r/LΩ (рад/с), если L измеряется в генри, а r в омах.

Из рассмотренного примера следует, что для нахождения аналитического выражения Z(jω) или Y(jω) как функции частоты следует задать входное напряжение U (или входной ток I) и найти входной ток I (или входное напряжение U), затем воспользоваться одним из выражений Z = U/I или Y = I/U.

Если известна структура и характер элементов цепи, то искомое выражение можно найти непосредственно, как это было сделано в примере 1.1. Полученное выражение обычно приводят к виду

где и полиномы, зависящие от переменной . После преобразований с комплексными слагаемыми всегда есть возможность записать исследуемую функцию в полярной (показательной) форме, выделяя зависимости АЧХ и ФЧХ.

В простейших неразветвленных rL и rС цепях иногда используют понятие граничной частоты . Граничной называется частота, при которой r = X, т.е. = r/L, или = 1/rС. Как следует из приведенного выше примера 1.1, на граничной частоте Z(ω) = 0.707r, а φ(ω) = 45˚.

Задача решена.