48
(4.7)
В выражении (4.7) первое слагаемое - Dx=Kx(0), второе слагаемое - Dx=Kx(0), третье слагаемое - 2Kx(T).
Пусть x(t) - стационарный сигнал. Он однороден во времени и его характеристики от него не зависят. Тогда
De = 2Kx(0) - 2Kx(T).
σ = |
De |
= |
2(Kx(0) − Kx(T )) |
(4.8) |
Методика определения шага дискретизации состоит в разрешении уравнения (4.8) относительно Т.
АКФ Кх(τ) является более содержательной характеристикой, чем эффективная полоса частот. Поэтому, определение шага дискретизации по уравнению (4.8) является более точным, чем по неравенству Берншейна.
Изменение частоты дискретизации. При решение различных задач обработки сигналов достаточно часто требуется изменение частоты дискретизации сигнала.
Пример – преобразование аудиозаписи из формата записи компакт-диска ( fдискр = 44,1 кГц) в формат цифровой магнитной записи R-DAT ( fдискр = 48 кГц)
и обратно.
Возможны следующие варианты:
1.Интерполяция – повышение частоты дискретизации в целое число раз (interpolation).
2.Прореживание или сэмплирование (decimation) – понижение частоты дискретизации в целое число раз.
3.Передискретизация (resampling) – изменение частоты дискретизации в произвольное (в том числе дробное) число раз.
4.2. Квантование непрерывных сигналов по уровню
Квантование необходимо для того, чтобы от непрерывного сигнала перейти к цифровому. Процесс квантования сводится к округлению бесконечного множества значений сигнала до ближайших оцифрованных значений, называемых уровнями квантования.
В отличии от временной дискретизации, когда в соответствии с теоремой Котельникова погрешность дискретизации может быть ≥ , квантование по уровню связано с возникновением неустранимой погрешности квантования.
Рассмотрим рисунок
|
49 |
|
|
|
h |
x |
вых |
|
|
|
|
|
|
|
|
|
h |
x |
вх |
|
|
|
|
|
Доказано, что погрешность квантования представляет собой случайную величину, равномерно распределенную в пределах шага h и аддитивную по отношению по отношению к квантованному сигналу.
Поэтому, вместо квантователя можно использовать эквивалентную схему
r кв
хвх 
+ 
хвых
1/h |
ωкв (r) |
|
|
r кв |
-h/2 |
0 |
h/2 |
|
Математическое ожидание mr = 0. Дисперсия погрешности квантования Dr = h2/12. СКО погрешности σr =h / 2
3.
Методика определения параметров квантования исходя из заданной
σr=(σr)доп
Пусть известен диапазон амплитудных значений сигнала |x|max. Необходимо найти число уровней квантования К и число двоичных
разрядов N.
1. По заданной погрешности квантования определяем шаг
h=2σr 
3.
2.Далее определяем число уровней квантования K= ]|x|max/h[.
3.И, наконец, находим число двоичных разрядов N=]lb K[.
50
Вносимая в результате аналого-цифрового преобразования среднее квадратичное отклонение ошибки составит
σ =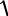 
σв2 +σ2r .
Равномерное квантование гарантирует, что динамический диапазон (или размах) шума квантования не превосходит величины шага квантования.
Однако для минимизации среднеквадратичного шума квантование необходимо, чтобы набор уровней квантования зависел от статистических свойств сигнала, а именно, от плотности вероятности значений сигнала в фиксированные моменты времени.
Иначе говоря, уровни квантования должны располагаться плотнее друг к другу в тех областях, где сигнал принимает значения с наибольшей вероятностью. Тогда весь динамический диапазон сигнала D разбивается на N зон квантования a0 ,a1,...,aN .
Если значение входного сигнала попадает в диапазон [ak−1,ak ], то ему соответствует значение bk .
Пусть сигнал имеет плотность вероятности P(x) и мы хотим
минимизировать дисперсию шума квантования. Среднее значение ошибки квантования e :
N ak |
N |
ak |
|
e = ∑ |
∫ |
(x −bk )P(x)dx = x − ∑bk |
∫ P(x)dx = x |
k=1 a |
k −1 |
k=1 |
a |
|
|
k −1 |
|
где x – математическое ожидание сигнала x , попадания значения сигнала в k -й диапазон квантования.
N
− ∑bk Pk ,
k=1
аPk – вероятность
|
N ak |
|
N |
ak |
N |
ak |
|
e 2 |
= ∑ |
∫ |
(x −bk )2 P(x)dx = x 2 |
− 2∑bk |
∫ xP(x)dx + ∑bk2 |
∫ P(x)dx |
|
|
k=1 a |
k −1 |
|
k=1 |
a |
k=1 |
a |
|
|
|
|
k −1 |
|
k −1 |
|
e 2 – средний квадрат ошибки.
Для минимизации e 2 необходимо, чтобы частное произведение этого выражения по ak и bk были бы равны 0.
В результате можно получить выражения для определения оптимальных значений параметров
|
|
ak |
|
|
|
|
|
∫ xP(x)dx |
|
= bk−1 + bk |
|
b |
= |
ak −1 |
; a |
||
a |
|||||
k |
|
k |
2 |
||
|
|
k |
|
||
|
|
∫ P(x)dx |
|
|
|
|
|
ak −1 |
|
|
Это же выражение обеспечивает и нулевое среднее значение шума квантования.
51
5. ОСНОВНЫЕ ТИПЫ ДИСКРЕТНЫХ АЛГОРИТМОВ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ
Математические методы обработки сигналов можно подразделить на три группы, если в основу классификации положить принцип формирования отдельного элемента (отсчета) результата по некоторой совокупности элементов (отсчетов) исходного сигнала [16].
Точечные преобразования – в таких преобразованиях обработка каждого элемента исходных данных производится независимо от соседнего. Иначе говоря, значение каждого отсчета результата определяется как функция от одного отсчета исходного сигнала, причем номера отсчетов сигнала и результата одинаковы.
Иначе говоря, пусть требуется обработать вектор из n отсчетов сигнала:
X = [x0 x1 |
x2 ... |
xn ] |
(5.2) |
||
и получить последовательность чисел: |
|
|
|
||
Y = [y0 y1 |
y2 ... |
yn ], |
|
(5.3) |
|
причем |
yi = f(xi) |
|
(5.4) |
||
Точечные преобразования |
просты и наименее |
||||
достаточно |
громоздки с |
||||
точки зрения вычислительных затрат. Если обрабатывается матрица размером N x N элементов отсчетов исходного двумерного сигнала, то вычислительная сложность процедуры точечных преобразований составит
Qт = N2 (БО),
где под базовой операцией (БО) понимается операция вида (5.4).
Локальные преобразования - при локальных преобразованиях обеспечивается формирование каждого элемента матрицы или вектора результата как функции от некоторого множества соседних элементов матрицы или вектора отсчетов исходного сигнала, составляющих некоторую локальную окрестность. При этом полагается, что местоположение вычисляемого отсчета результата (или текущий индекс элемента) задается координатами (или текущими индексами) центрального элемента локальной окрестности. Для формирования следующего элемента матрицы результата выполняется смещение окрестности вдоль строки матрицы исходных данных или вдоль исходного вектора. Такая перемещаемая окрестность часто носит название окна сканирования. При обработке матрицы исходных данных после прохождения всей строки матрицы исходных данных окно сканирования смещается на одну строку и возвращается в начало следующей строки, после чего продолжается обработка. Просматриваемая при перемещении окна сканирования полоса
строк матрицы носит название полосы сканирования. Иначе говоря, |
при такой |
обработке |
|
yi = F(X^ ) ; X^ = {xi-m/2, xi-m/2+1, ..., xi, ..., xi+m/2-1, xi+m/2}, |
(5.5) |
где i = 0,N-1 - индекс отсчета результата , m - размер окна сканирования. Если
i<m/2 или i>N-m/2, что имеет место на практике при обработке начальных и конечных отсчетов вектора исходного сигнала, то элементы вектора исходных данных с "недостающими" индексами полагаются равными нулю.