
Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov
.pdf
m |
|
|
|
N |
2 |
~2 |
i |
(−1) |
i |
4 |
|
(x, y)= |
|
|
|||||||||||
∑Ei |
∑ |
(ψη |
+ϕγ |
) |
|
∑ Cη,γ ,ξ (s) Bη,γ ,ξ |
||||||
i=1 |
|
η,γ =1 |
|
|
|
|
|
ξ =1 |
|
|
||
|
N |
|
|
4 |
|
|
|
|
|
N |
4 |
|
= ∑ Kη,γ |
∑ Cη,γ ,ξ (s) Bη,γ ,ξ (x, y)− E0 |
∑ ∑ Cη,γ ,ξ (s) Bη,γ ,ξ (x, y). |
||||||||||
η,γ =1 |
ξ =1 |
|
|
|
|
η,γ =1ξ =1 |
||||||
Преобразуя, придем к следующему результату:
|
|
N |
4 |
|
|
|
|
|
|
m |
2 |
~2 |
) |
i |
|
i |
|
|
|
∑ ∑ Cη |
γ ξ (s) Bη |
|
|
|
|
|
(−1) |
− |
|||||||
|
|
γ ξ (x, y) |
∑(ψη |
+ϕγ |
|
|
|||||||||||
|
|
|
, |
, |
, |
, |
|
|
|
|
|
|
|
|
|
|
|
|
η,γ =1ξ =1 |
|
(η,γ = |
|
). |
i=1 |
|
|
|
|
|
|
|
||||
где |
|
|
= Kη,γ |
− E0 , |
|
|
|
|
|
|
|
|
|
|
|||
|
η,γ |
1, N |
|
|
|
|
|
|
|
|
|
||||||
K |
|
|
|
|
|
|
|
|
|
||||||||
Kη,γ = 0 ,
Приравнивая выражение в фигурных скобках к нулю, получим систему уравнений
|
|
|
|
2 |
|
~2 |
) |
i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(η,γ =1, N ). |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
(−1) |
− Kη,γ = 0, |
|
|
|
|
|
(2.39) |
||||||||||||||||||||||||||||||||||||
∑Ei |
(ψη |
+ϕγ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Представим (2.39) в матричной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
Ψ E − K = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.40) |
|
|
|
|
|
||||||||||||||
где |
|
+ϕ1 ); |
L (ψ1 |
+ϕ1 ) |
|
|
(−1) |
|
|
; K |
(ψ1 |
+ϕ1 |
) |
|
(−1) |
|
; |
|
||||||||||||||||||||||||||||
−(ψ1 |
i |
|
i |
m |
m |
|
||||||||||||||||||||||||||||||||||||||||
|
2 |
~2 |
|
|
|
|
|
|
|
|
2 |
|
~2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
~2 |
|
|
|
|
||||||||||||||
2 |
~2 |
|
|
|
|
|
|
|
|
|
2 |
|
~2 |
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
2 |
~2 |
|
m |
|
m |
|
||||||||||
Ψ= −(ψ1 |
+ϕ2 ); |
K (ψ1 |
+ϕ2 ) |
|
|
(−1) |
|
|
; K (ψ1 |
+ϕ2 ) |
|
(−1) |
|
; |
; |
|||||||||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
||||||||||
|
2 |
~2 |
); |
K (ψ |
2 |
|
|
~2 |
) |
i |
(−1) |
i |
; K |
|
(ψ |
2 |
~2 |
) |
m |
(−1) |
m |
|
||||||||||||||||||||||||
−(ψ |
N |
+ϕ |
N |
N1 |
+ϕ |
N |
|
|
|
|
N |
+ϕ |
N |
|
|
; |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1,1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
E = |
E |
2 |
; |
|
|
|
|
|
K = |
|
|
K |
2,1 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
K |
N,N |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Определитель матрицы Ψ сводится к определителю Вандермонда, который отличен от нуля. Следовательно, Матрица Ψ неособенная, а значит решение уравнения (2.40) существует, что и требовалось доказать.
Таким образом, используя уравнение (2.40), можно определить значения коэффициентов (Ei (i =1,m)) распределенного блока, преобразующего воздействие (2.36) в (2.37).
70
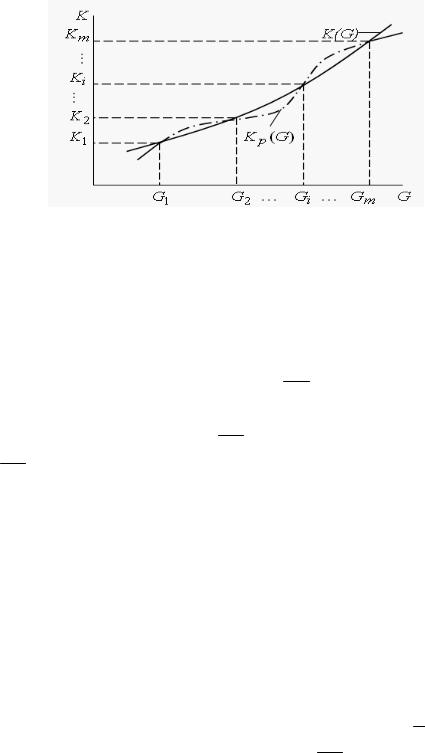
Рис. 2.14. График K.
Следствие из доказанного утверждения
Положим, что необходимо реализовать статический коэффициент усиления, график которого приведен на Рис. 2.14. При этом входное воздействие полагается заданным в виде (2.36). Определим спектр
значений координаты G при изменении η,γ =1, N
G1 (η =1, γ =1); G2 (η =1, γ = 2); KGm (η = N, γ = N).
Для вычисленных значений Gi (1,m) по графику определим значения
K(Gi ) (i =1,m) . Выберем E0 = K(G1) .
Подставляя вектор значений K в уравнение (2.40), определим вектор
коэффициентов |
|
|
|
При этом матрица Ψ с использованием |
|||||||||
|
|
|
|
|
|
||||||||
Ei (i =1,m) . |
|||||||||||||
обобщенной координаты G может быть представлена в виде |
|||||||||||||
|
G (−1); |
K Gi |
(−1)i ; |
K Gm |
(−1)m; |
||||||||
|
|
1 |
(−1); |
1 |
(−1)i ; |
1 |
|
|
|||||
|
G |
2 |
K Gi |
K Gm |
(−1)m; |
||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
. |
||
|
|
|
|
|
|
K |
|
|
|
K |
|
|
|
|
|
|
|
|
|
i |
|
i |
; |
m |
(−1) |
m |
|
|
Gm (−1); |
K Gm (−1) |
|
K Gm |
; |
||||||||
Распределенный блок с вычисленными параметрами (Еi ) реализует коэффициент усиления K p (G) . В узлах Gi (i =1,m) значения K p (G) и K(G) (см. Рис. 2.14) совпадают.
2.2.2 Распределенный фильтр
Пусть требуется определить структуру и параметры распределенного блока, статический коэффициент усиления которого приведен на Рис. 2.15.
71

Рассматриваемый распределенный блок выделяет из входного воздействия совокупность пространственных мод, для которых выполняется условие G2 ≤ G ≤ G3 , т.е. по существу является
распределенным фильтром.
Рис. 2.15. График коэффициента усиления.
Структуру распределенного фильтра будем формировать из рассмотренных в п. 3.1 распределенных звеньев. Для реализации статического коэффициента в виде кривой 1 (см. Рис. 2.16) будем использовать пространственно-усилительное звено:
~ |
|
n |
|
−1 |
|
1 |
2 |
|
|
||
W |
= E |
|
1 |
|
|
− |
|
|
. |
||
|
|
|
n |
||||||||
1 |
1 |
|
n |
|
|
|
|||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
Значения параметров E1 и n1 выбираются из следующих условий:
|
|
|
|
|
|
|
n1 −1 |
|
G2 |
|
|
|
|
|
|
20 lg E = |
|
, |
20 |
lg E |
+ |
|
= |
|
, |
||||||
1 |
n |
n |
|
2 |
|||||||||||
1 |
|
|
|
1 |
|
|
|
|
|
||||||
где 1 и |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
||
2 - заданные числа (см. Рис. 2.16). |
|
|
|||||||||||||
Определив из графиков (см. Рис. 2.16) |
1= - 10 дБ; |
|
2 =20 дБ; |
||||||||||||
lgG = 3,2, получим: E1 = 0,316 ; n1 = 51,8 .
Статические коэффициенты усиления, графики которых заданы в виде кривых 2 и 3 (см. Рис. 2.16), будем реализовывать с помощью устройства,
~
рассмотренного в п. 3.1 (см. Рис. 2.17), где передаточные функции W2 и
~
W3 имеют вид:
72

~ |
|
|
|
n |
2 |
−1 |
|
1 |
2 |
|
|
~ |
|
|
n |
|
−1 |
|
1 |
2 |
|
|
|||||
W |
= E |
|
|
|
|
|
|
− |
|
|
|
; |
W |
= E |
|
|
3 |
|
|
− |
|
|
. |
||||
2 |
|
n |
|
|
n |
|
|
|
|
|
n |
||||||||||||||||
2 |
|
|
2 |
|
|
2 |
|
|
3 |
3 |
|
|
n |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
||||
|
Рис. 2.16. Синтез фильтра. |
Выберем произвольные точки на кривых 2 и 3 (см. Рис. 2.16) |
|
A{lgG4 , 4}, B {lg G 5 , 5 |
}, (G4 > G2; G5 > G3) . |
Используя статический коэффициент передачи усилительного звена, включенного в обратную соотношения между параметрами точек A и B:
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
4 = 20 lg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
n2 |
−1 |
|
|
G4 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
+ K2 |
E2 |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
n2 |
|
|
|
|
n2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
K3 |
|
|
|
|
|
|
|
|||
|
5 |
= 20 lg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
~ |
|
|
|
|
|
n |
− |
1 |
|
G |
|
|||||||||
|
|
|
|
|
1 + K |
|
E |
|
3 |
|
|
|
+ |
5 |
|
|
|||||||
|
|
|
|
3 |
3 n |
|
|
n |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|||
К полученным |
уравнениям |
|
допишем |
|
условие, |
||||||||||||||||||
20 lg K(G) = 0 или
пространственносвязь, запишем
(2.41)
что при G → 0
73
|
|
|
~ |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
K2 |
|
|
|
|
|
=1, |
|
|
K3 |
|
|
=1. |
|||
|
~ |
|
|
|
|
n |
2 |
−1 |
~ |
|
|
|
n |
|
−1 |
|||
1 + K |
2 |
E |
2 |
|
|
|
|
|
1 + K |
3 |
E |
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
n2 |
|
|
3 |
|
n3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(2.42)
Рассматривая совместно (2.41) и (2.42), можно определить значения
~
параметров Ki , Ei , ni (i=2,3).
Полагая в соотношениях (2.42) n2 >>1 и |
n3 >>1, преобразуем их к |
||||
виду |
|
~ |
|
|
|
~ |
|
|
|
|
|
K |
|
K |
|
|
|
~ 2 |
=1, |
~ 3 |
=1. |
|
|
1 + K2 E2 |
|
1 + K3 E3 |
|
|
|
|
|
|
~ |
~ |
= 2 , |
Используя полученные соотношения, выберем значения K2 |
= K3 |
||||
E2 = E3 = 0,5 .
|
|
Рис. 2.17. Структурная схема фильтра |
|
|
|
|
|
Определив из графиков (см. Рис. 2.16) |
4 = −10дб; 5 = −12дб; |
||
G |
|
|
~ |
|
, |
4 |
=104,8 ; G =105,8 и подставив вместе с вычисленными значениями K |
i |
|||
|
5 |
|
|
||
Ei |
(i=2, 3) в уравнения (2.41), получим n2 = 9983, |
n3 = 79246 . |
|
|
|
Моделирование работы распределенного фильтра было осуществлено на ЭВМ. По результатам моделирования были определены значения коэффициентов усиления фильтра в зависимости от Gi (i=1,2 …) (см. Рис.
2.18).
74
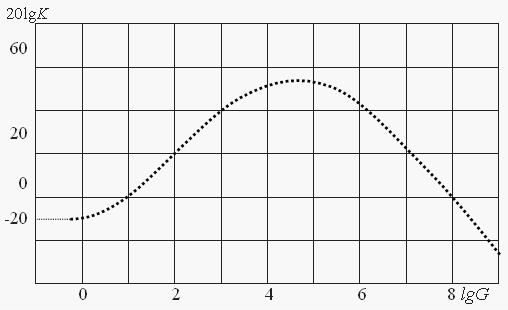
Рис. 2.18. Результаты моделирования.
2.2.3 Распределенный регулятор прямого действия
Область применения распределенных регуляторов прямого действия может быть достаточно широкой. Эти регуляторы управляют «живым» сечением канала текущей жидкости и используются в системах подвода (отвода) тепловой энергии.
Положим, что требуется отвести энергию (q) от поверхности оболочки, показанной на Рис. 2.19, при этом интенсивность тепловой энергии меняется случайным образом и в различных точках поверхности оболочки она различна. Требуется разработать систему управления, обеспечивающую отвод тепловой энергии от оболочки.
Покроем оболочку с внутренней стороны специальными «секциями». В зависимости от интенсивности теплового потока (q) теплоноситель каждой секции нагревается (охлаждается), а следовательно регулятор (биметаллическая пластинка), помещенный в поток теплоносителя, увеличивает (уменьшает) живое сечение каналов, осуществляя регулирование расхода теплоносителя через заданную секцию. Блокпоглотитель энергии перерабатывает тепловую энергию в другие виды энергии (см. Рис. 2.19). Блок-насос поддерживает заданное значение
перепада давления P теплоносителя.
Как известно, биметаллическая пластинка (Б.П.) изготовлена из материалов А – активного (обладающим большим коэффициентом теплового расширения) и В – пассивного (обладающим малым коэффициентом расширения). Пусть Б.П. помещена в поток теплонесущей жидкости. При этом омывается потоком одна плоскость Б.П., а другая
75
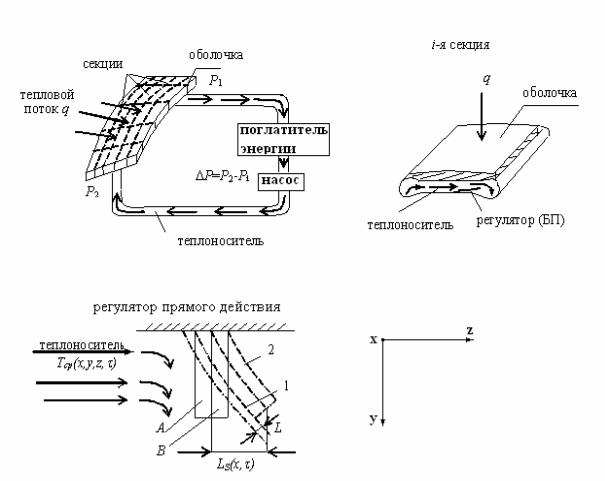
находится в «тени» потока (см. Рис. 2.19). У обтекаемой потоком поверхности Б.П. формируется пограничный слой, толщина которого зависит от физических свойств теплонесущей жидкости. Изменение температурного поля на границе пограничного слоя приводит к изменению температуры внутри слоя, а следовательно изменяется температурное поле Б.П.
Пусть один конец Б.П. закреплен, а второй свободен. Изменение температурного поля Б.П. приводит к перемещению свободного конца пластинки на величину Ls (x,τ) (см. Рис. 2.19).
В качестве входного воздействия в регуляторе (Б.П.) выберем температуру теплонесущей жидкости на границе пограничного слоя.
Tср(xc , yc , zc ,τ) =T1(xc , yc , zc ,τ) ,
где T1(xc , yc , zc ,τ) - температурное поле пограничного слоя; xc , yc , zc - параметры пограничного слоя, толщина которого равна L.
Рис. 2.19. Распределенный регулятор прямого действия
76

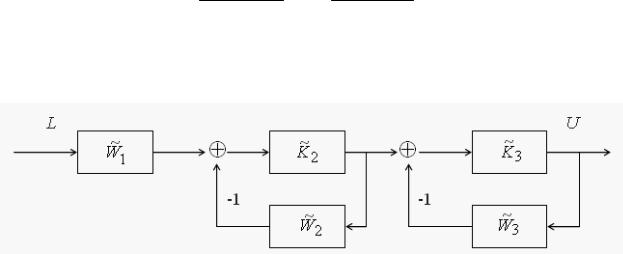
В качестве функции выхода будет перемещение Ls (x,τ) . Структурная схема рассматриваемого регулятора приведена на Рис. 2.20.
Рис. 2.20. Структурная схема регулятора прямого действия.
Рассмотрим другие конструкции регуляторов прямого действия, управляющих «живым» сечением каналов текущих жидкостей с целью регулирования скорости подвода (отвода) тепловой энергии.
1. Конструкции на основе эластичных резервуаров (см. Рис. 2.21, а). Изменение температуры теплоносителя на величину T приводит к изменению объема эластичного резервуара на величину V, что в свою очередь приводит к изменению площади живого сечения на величину S. 2. Конструкции на основе биметаллических пластин (см. Рис. 2.21, б). Канал - 2, по которому движется теплоноситель-3, изготовлен из материала с низким коэффициентом линейного расширения. Снаружи канала нанесены пластины-1 активного материала, имеющего большой коэффициент линейного расширения. При изменении температуры теплоносителя происходит изменение профиля поперечного сечения
канала (изменение «живого» сечения канала).
Рис. 2.21. Конструкции регуляторов прямого действия.
В рассматриваемой конструкции активный материал может быть нанесен как на наружную поверхность канала, так и на внутреннюю поверхность.
Для построения динамических характеристик рассматриваемого регулятора составим его математическую модель.
Математическая модель рассматриваемых регуляторов может быть представлена в виде описания двух процессов – процесса изменения теплового поля, следствием которого будет механическое перемещение.
77
Опишем тепловые процессы, протекающие в пограничном слое и в
Б.П.
При описании тепловых процессов будем полагать:
-боковые грани Б.П., за исключением поверхностей 1 и 2 (см. Рис. 2.19), не влияют на процессы, протекающие внутри Б.П.. Отметим, что рассматриваемые боковые грани имеют малую площадь боковой поверхности по сравнению с площадью поверхностей 1 и 2;
-тепловые процессы вблизи плоскости Б.П., находящейся в «тени» потока теплоносителя (см. Рис. 2.19, поверхность 2), не влияют на тепловые процессы Б.П.;
-Б.П. имеет прямоугольную форму.
Сучетом принятых допущений математическая модель тепловых процессов в Б.П. может быть записана в виде
∂T |
|
|
∂2T |
+ |
∂2T |
+ |
∂2T |
|
, (i=1,2,3), |
|||
i = a |
|
|
i |
|
i |
|
i |
|||||
∂T |
i |
|
∂x |
2 |
|
∂y |
2 |
|
∂z |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
(2.43)
0 < x < Lx ; 0 < y < Ly ; Zi+1 < z < Zi (z0 = 0) ,
где Ti (x, y, z,τ) - температурное поле i-ой среды (i =1 – пограничный слой, i=2 – материал А, i=3 – материал В); ai коэффициенты температуропроводности i-ой среды; Lx , Ly , Zi - заданные значения
(координаты границ раздела сред).
Граничные условия для системы уравнений (2.43), отражающие неразрывность тепловых полей и тепловых потоков на границах раздела сред, записывается в виде следующих соотношений
T1(x, y,0,τ) =Tср(x, y, zc ,τ), (zc = 0) ; |
|
|||||||||
Ti (x, y, zi ,τ) =Ti+1(x, y, zi ,τ), (i =1,2). |
(2.44) |
|
||||||||
|
|
|||||||||
λi |
∂Ti (x, y, zi ,τ) |
|
= λi+1 |
∂Ti+1 (x, y, zi ,τ) |
, (i=1,2); |
(2.45) |
||||
|
|
∂z |
|
∂z |
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 < x < Lx ; 0 < y < Ly ; |
|
||||
|
|
∂T2 |
(x, y, z,τ) |
|
= 0 |
|
|
, z1 < z < z2; 0 < y < Ly ; |
|
|
|
|
|
|
|
|
|||||
|
|
|
∂x |
|
|
|
|
|||
|
|
|
|
|
|
x=0, x=Lx |
|
|
||
|
|
|
|
|
|
|
|
|
||
78

|
|
|
|
∂T3(x, y, z3,τ) |
= 0 , 0 < x < Lx ; 0 < y < Ly ; |
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
∂T3 |
(x, y, z,τ) |
= 0 |
|
|
|
|
, z2 < z < z3; 0 < y < Ly ; |
||||
|
|
|
|
|
||||||||
|
|
|
∂x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
x=0, x=Lx |
|||||
∂T3 |
(x, y, z3 |
,τ) |
|
|
||||||||
= 0 |
|
|
, 0 < x < Lx ; z2 < z < z3, |
|||||||||
|
|
|||||||||||
|
|
|
∂y |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
y=0, y=Ly |
|||
|
|
|
|
|
|
|
|
|
|
|
||
где λi - коэффициент теплопроводности i-ой среды (i =1,3) .
Для частотного анализа блока 1 (см. Рис. 2.20) положим, что входное воздействие Tcp (x, y, zcp ,τ) может быть представлено в виде
|
|
∞ |
|
|
||
Tср(x, y, z,τ) = |
∑exp( jϖτ) cos(ψη x) cos(ϕγ |
y) , |
(2.48) |
|||
|
η,γ =1 |
|
|
|||
где ψη =πη |
, ϕγ |
=πγ , (η,γ = |
|
) , ω - круговая частота. |
|
|
1, ∞ |
|
|||||
Lx |
|
Ly |
|
|
||
(Вид разложения в ряд Фурье согласуется с граничными условиями).
Реакцию температурного поля на каждую составляющую ряда Фурье (2.48) будем искать в виде
Ti,η,γ (x, y, z,τ) = Hi,η,γ (z, iω) exp( jωτ) cos(ψη x) cos(ϕγ y) , (2.49)
(i =1,3; η,γ =1, ∞),
где Hi,η,γ (z, iω) - функция, подлежащая определению.
Подставляя (2.49) в (2.43) и преобразуя, получим
|
|
|
∂2 Hi,η,γ (z, jω) |
|
||
jω H i,η,γ (z, jω) = ai |
(−ψη2 |
−ϕγ2 ) Hi,η,γ (z, jω) + |
|
|
, (2.50) |
|
∂z 2 |
||||||
|
|
|
|
|
||
|
|
|
|
|
|
|
(i =1,2;η,γ =1, ∞) .
Преобразуя (2.50), придем к следующему результату:
79
