Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov

.pdf

Скачиваний:

Добавлен:

21.03.2016

Размер:

3.83 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 213 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Комплексный коэффициент передачи по η −ой (η =1,∞) составляющей входного воздействия может быть определен из следующего соотношения:


	~		J0	*
	Tη x, R, jωτ		J0	γη R
Wη (jω)=					,	(1.29)
Wη (jω)=	qη sin(ψη x)exp(jωτ)	=	J0 (γηR)		,	(1.29)

(η =1,∞).

Примечание: непосредственно из (1.29) следует, что комплексный передаточный коэффициент по каждой составляющей моде входного воздействия не зависит от пространственных координат.

1.1.5 Понятие пространственно-инвариантных объектов

Положим, что имеется распределенный объект, математическая модель которого описывается уравнениями (1.1). Пусть входное воздействие представимо в виде ряда (1.16).

Объект автоматического управления, представленный в форме (1.1), называется пространственно-инвариантным, если комплексный передаточный коэффициент по каждой составляющей входного воздействия не зависит от пространственных координат.

Математически это определение означает:

Wμ,i,η,γ ,ξ (x, y, jω)=Wμ,i,η,γ ,ξ (jω),

(μ =1,m; i =1,n; η,γ =1,∞; ξ =1,4).

Интерпретация введенного определения на языке структурных схем заключается в следующем: объект управления, удовлетворяющий определению, может быть представлен совокупностью независимых блоков с комплексными передаточными коэффициентами Wμ,i,η,γ ,ξ (jω),

(μ =1,m; i =1,n; η,γ =1,∞; ξ =1,4).

На физическом уровне определение означает, что составляющая входного воздействия, проходя через объект управления, изменяет только амплитуду пространственной моды.

На математическом уровне – собственные функции оператора объекта могут быть представлены в виде комбинации sin() и cos() (функциями

Bμ,η,γ ,ξ (x, y)).

Выделим свойства, которым должны обладать передаточные функции, полученные на основе функций Грина (см. п.1.2.2), чтобы объект относился к классу пространственно-инвариантных. Положим, что

входное воздействие на объект управления представлено в виде ряда (1.16). Тогда реакция объекта на каждую пространственную моду может быть записана в виде:

Qη,γ ,ξ (x, y, jω)= ∫∫W (x, y, x1, y1, jω) Cη,γ ,ξ (jω) Bη,γ ,ξ (x1, y1)dx1dy1 , (1.30)

где x1, y1 D1 - область распределения входных воздействий.
(Для простоты рассматриваем скалярное входное воздействие								μ =1.)
Комплексный		передаточный			коэффициент	по		каждой
пространственной моде будет равен:
W	(x, y, jω)=		Qη,γ ,ξ (x, y, jω)		Cη,γ ,ξ (jω) Bη,γ ,ξ	(x, y)
η,γ ,ξ							y1 → y).
При этом наложим области функций входа и выхода (x1 → x,
Положим, что
	Qη,γ ,ξ (x, y, jω)=			Q1,η,γ ,ξ (jω) Bη,γ ,ξ (x, y),		(1.31)
тогда Wη,γ ,ξ (x, y,		jω)=Wη,γ ,ξ (jω), т.е.			объект принадлежит		к	классу
пространственно-инвариантных.
Условие (1.31) выполняется если
		~				, y1 ),
W (x, y, x1, y1, jω)= ∑W η,γ ,ξ (jω) Wη,γ ,ξ (x, y, x1
			η,γ ,ξ

где Wη,γ ,ξ (x, y, x1, y1) - представляется в виде произведения ортогональных

функций, аналогичных (1.17). Полученные условия пространственной инвариантности распределенного объекта могут быть перенесены и на функции Грина.

Пример.

Определим комплексный передаточный коэффициент по пространственным модам для объекта, передаточная функция которого приведена в примере п.1.2.2.

Положим,		что входное воздействие распределено по области
	D1 ,
ρ,ν,ϑ =ϑ		а функция выхода x, y, z = z D2 . Где ϑ , z - фиксированные

значения координат ϑ, z . Тогда передаточная функция может быть записана в виде:

∞

()

∞

(z )

∑ Bk,m

∑

W (x, y, z, ρ,ν,ϑ , s)=

k,m

n=1

+ a

l 2

где

sin

k π x

sin

π y

sin

k π ρ

sin

m π ν

Bk,m ()

n π z

n (z )= sin

sin

n π ϑ

Qη,γ ,ξ (x, y, jω)= ∫ ∫W (x, y, z, ρ,ν,ϑ

, jω) Cη,γ ,ξ (jω) Bη,γ ,ξ (ρ,ν )dρdν

Учитывая ортогональность подинтегральных функций, получим:

∞

Bη,γ () ∑

n (z)

(x, y, z, jω)=

Qη,γ ,ξ =1

n=1

jω + a

l 2

Комплексный

передаточный

коэффициент

по

пространственной моде равен (ρ → x,ν → y)

Wη,γ

,ξ =1(x, y, jω)=

Qη,γ ,ξ =1(x, y, z, jω)

Cη,γ ,ξ =1(jω) Bη,γ ,ξ =1(x, y)

∞

∑

n (z )

n=1

l1 l2 l3

jω

+ a

2 +

Cη,γ ,ξ

каждой

=1(jω)

(1.32)

Как следует из (1.32) Wη,γ ,ξ =1(x, y, jω)=Wη,γ ,ξ =1(jω), т.е. объект принадлежит к классу пространственно-инвариантных.

1.1.6 Пространственно – инвариантные системы

Рассмотрим систему автоматического управления, составленную из объекта и регулятора.

Математическая модель объекта имеет вид:

∂Τ

∂n1

∂Τ

∂n2 Τ

∂Τ

∂n3 Τ

= L

(Τ ;

i ;...

;

i ;...

i ;

i ;...

i ),

(1.33)

∂τ

∂x

∂xn1

∂y

∂yn2

∂z

∂zn3

x, y, z V ,

(i=1,n),

∂y h3

n
θχ (x, y,τ) =∑aiΤi (x, y, zχ ,τ),	(1.34)

i=1

(χ =1,m),

где θχ(x,y,τ) - регулируемые переменные (χ =1, m) ; ai - заданные коэффициенты (i =1,n).

(Для простоты полагаем, что ai (i =1,n) принимают значения либо

0,либо 1, причем ∑ai =1.)

i=1

Граничные условия для системы уравнений (1.34) описываются соотношениями:

L2,i [Τi (χ, y, z,τ),	Τi+1(χ, y,τ)=0,]			(1.35)
x, y, z Г1,i		(i =
			1, n −1),
~				(1.36)
Li,τ =[Τi (x,y,z,τ)]=0,		~
x, y, z Г2,i				~
	(i =1, n;
			j	=1, n ),
~	αμ(x, y,τ)]=0,			(1.37)
Li,μ [Τi (x, y, zμ ,τ);
x, y Г3,μ′		(μ =
				1, m ),

Математическая модель регулятора:

Lp ,μ (Fp ,μ ;

∂Fp

,μ

;...

∂h1

Fp ,μ

;

∂Fp ,μ

;...

∂h2 Fp ,μ

;

∂τ

∂x

∂τ 1

∂x

∂Fp ,μ

∂h3 Fp ,μ

∂U μ

;...

;U μ ;

;...

∂h1U μ

;

(1.38)

∂y

∂τ

∂y 3

∂τ h1

∂U μ		~
∂U μ	;...	∂h2U μ
		~
∂x		~
∂x		∂x h2

; ∂∂Uyμ ;... ∂h3U μ ) = 0,

x, y Гp,μ′	(μ =
		1, m),

Граничные условия для системы уравнений (1.38):

~
Lpμ (Fp,μ;Uμ ) = 0 , x , y Г~ p , μ	(1.39)

( μ = 1, m; ~ 1, m ),

μ =

Уравнения связей, обеспечивающих замыкание системы (см. рис. 1.5), имеют вид:

U p,μ (x, y,τ ) = αμ (x, y,τ ),(μ =1, m)

Fp,μ (x, y,τ ) = Fμ (x, y,τ ) −θμ (x, y,τ ),

Где

(μ = 1, m) - задающие воздействия.

Полагая, что задающие воздействия Fμ (x, y,τ ), в ряды Фурье, представим их в виде:

(1.40)

(1.41)

Fμ (x, y,τ ),

(μ = 1, m) разложимы

∞

(x, y),

Fμ (x, y,τ) = ∑∑Cμ,η,γ ,ξ (τ) * Bμ,η,γ ,ξ

(1.42)

η,γ =1ξ=1

(μ =

1,m

где

xF ,μ −yF ,μ

∫

Cμ,η,γ,ξ (τ) =

Fμ (x, y,τ) * Bμ,η,y,ξ (x, y)dxdy,

(1.43)

F,μ

F,μ −F ,μ −yF ,μ

μ =

;η,γ =

,ξ =

1, m

1,∞

1,4);

Bμ,η,γ ,1(χ, y) = cos(ψF,η,μ * x)*cos(ϕF,μ,γ * y);

(χ, y)

Bμ,η,γ ,2

=sin(ψF,η,μ * x)*cos(ϕF,μ,γ * y);;

Рисунок 1.5. Система управления.

Bμ,η,γ ,3 (x, y)

Bμ,η,γ ,4 (x, y)

~
= cos(ψF,η,μ * x)sin(ϕF,μ,γ y);	(1.44)
~	(1.44)
=sin(ψF ,η,μ * x)sin(ϕF,μ,γ y)

	(μ =				η,γ =
			1,m;
						1,∞);
ψ F , μ ,η	=	π *η		;	ϕ~F , μγ =		π * γ	;

		xF , μ					γ F , μ

(μ =1, m; η,γ =1,∞);

xF,μ; yF,μ;(μ =1,m) - заданные числа.

Для частотного анализа системы положим в (1.42)

~	~	jωτ	,
Cμ,η,γ ,ξ	(τ) = qμ,η,γ ,ξ *e		,	(1.45)

(μ =1, m;η,γ =1,∞;ξ =1,4),
(μ =1, m;η,γ =1,∞;ξ =1,4),

где

qμ,η,γ,ξ (μ =1,m;η,γ =1,∞;ξ =1,4) - фиксированные значения.

Пусть реакция системы по

χ − ой регулируемой переменной

(χ =

) на η , γ , ξ

1,m

( μ =

;η , γ =

; ξ =

) пространственную

1, m

1, ∞

1,4

μ−го (μ =

моду

1, m)

входного воздействия определена:

(x, y, jω)*ejωτ.

χ,μ,η,γ,ξ

Комплексный передаточный коэффициент системы для χ − ой (χ =1,m)

регулируемой переменной

по

η , γ , ξ -ой

(η,γ =

1,∞

;ξ =

1,4

)

пространственной моде μ−го

(μ =

1, m)

входного

воздействия имеет

вид:

(x, y, jω)

Φμ,χ,η,γ,ξ (x, y, jω) =

μ,χ,η,γ,ξ

(1.46)

qμ,χ,η,γ,ξ *Bμ,χ,η,γ,ξ (x, y)

(χ, μ =1,m;η, y =1,∞;ξ =1,4)

Система управления, представленная в форме (1.33) – (1.41), является пространственно – инвариантной, если комплексный передаточный коэффициент

Φμ,χ,η,γ ,ξ (x, y, jω) = Φμ,χ,η,γ,ξ ( jω) ,

(1.47)

(χ, μ =1,m;η, y =1,∞;ξ =1,4)

Пространственно-инвариантная система обладает таким же свойством как и пространственно-инвариантный объект.

Введем понятие пространственной совместимости.

Определение: система обладает свойством пространственной совместимости, если соответствующие пространственные моды разложения входных сигналов регулятора и объекта совпадают.

Математически это определение означает:

=~ =~ =

Bμ,η,γ,ξ(x,y) Bμ,η,γ,ξ(x,y) Bμ,η,γ,ξ(x,y) Bη,γ,ξ(x,y), (1.48)

(χ, μ =1,m;η, y =1,∞;ξ =1,4)

Физический смысл определения состоит в том, что области распределения входных воздействий регулятора и объекта при наложении совпадают. При этом состояние входных воздействий на границах рассмотренных областей описывается одинаковыми условиями.

Утверждение . Для того, чтобы система автоматического управления была пространственно-инвариантной, достаточно, чтобы объект и регулятор были пространственно-инвариантными и система обладала свойством пространственной совместимости.

Доказательство.

Пусть для системы управления описываемой уравнениями (1.33) – (1.41), выполняются условия:

а) объект пространственно-инвариантный, т.е.


Wμ,i,η,γ ,ξ (x, y, jω) =Wμ,i,η,γ ,ξ ( jω),								(1.49)
( χ , μ =			;η , y =		; ξ =		)
		1, m		1, ∞		1,4
б) регулятор пространственно-инвариантный:
Rμ,η,γ ,ξ (x, y, jω) = Rμ,η,γ ,ξ ( jω),								(1.50)
( χ , μ =			;η , y =		; ξ =		)
	1, m			1, ∞		1,4

в) система обладает свойством пространственной совместимости:

~	~	(1.51)
Bμ,η,γ,ξ (x, y) =Bμ,η,γ,ξ (x, y) =Bμ,η,γ,ξ (x, y) =Bη,γ,ξ (x, y),

( χ , μ = 1, m ;η , y = 1, ∞; ξ = 1,4)

Разомкнем систему на входе регулятора. Подадим на вход регулятора воздействие

jωτ

*Bη, y,ξ (x, y),

(1.52)

Fp,m (x, y, jω) =qμ *e

где qμ

(μ =1,m;) - заданные числа;

η , γ , ξ

- фиксированные целые числа;

Согласно (1.50),

функции U

(μ =

) могут быть найдены

μ,η,γ

,ξ

1,m

из выражения:

(x, y, jω) = R

( jω)*q

*e jωτ *B

(x, y), (1.53)

μ,η,γ,ξ

η,γ,ξ

(μ =1,m).

Функции Uμ (x, y, jω) и αμ (x, y, jω) связаны соотношением (1.40)

(μ =1,m).

Функции регулируемых переменных θχ (χ, y, jω), согласно (1.34), с учетом (1.49), могут быть определены следующим образом:

θ (x, y, jω) = ∑ W			( jω)* R		( jω)* F (x, y, jω), (1,54)
	m	μ, χ,η,γ ,ξ
χ	μ=1	μ, χ,η,γ ,ξ		μ,η,γ ,ξ	p,μ
	μ=1

(μ =1,m).

Рассмотрим замкнутую систему автоматического управления (см. рис. 1.5). Подадим на вход системы задающее воздействие


	~		*e	jωτ	*Bη,γ,ξ		(x, y),		(1.55)
		Fμ =qμ	*e		*Bη,γ,ξ		(x, y),		(1.55)
					(μ =			).
~					(μ =	1,m		).
~	(μ =1,m) - заданные числа.
где qμ	(μ =1,m) - заданные числа.
					27

Согласно (1.41), входное воздействие в регулятор:

		~	*e	jωτ	* Bη,γ ,ξ (x, y)*θμ (x, y, jω),
Fp,μ (x, y, jω) = qμ			*e		* Bη,γ ,ξ (x, y)*θμ (x, y, jω),
				(μ =			).
				(μ =		1,m	).
Подставляя (1.56) в (1.54) с учетом (1.41), получим:
θμ (x, y, jω) =		m
θμ (x, y, jω) =		∑ Wμ,χ,η,γ,ξ ( jω)Rμ,η,γ,ξ ( jω)
~	μ=1
~		jωτ	Bη,γ,ξ (x, y)θμ (x, y, jω),
qμ *e			Bη,γ,ξ (x, y)θμ (x, y, jω),

(μ =1,m).

Представим систему уравнений (1.57) в матричной форме:

(1.56)

(1.57)

(x, y, jω) =(R

( jω)*W

( jω))T * F(x, y, jω) −θ(x, y, jω)),

η,γ,ξ

(1.58)

Rη,γ,ξ ( jω) =diag

Rμ,η,γ,ξ

(μ =

);

где

1,m

Wη,γ,ξ ( jω) =

, (μ =

);

Wμ,χ,η,γ,ξ ( jω)

1,m

F(x, y, jω) =

Fμ (x, y, jω)

(μ =

);

1,m

θ(x, y, jω) =

θμ (x, y, jω)

(μ =

1,m

Решая уравнение (1.58) , найдем функцию θ(x, y, jω):

θ(x, y, jω) =Φη,γ,ξ ( jω)*F(x, y, jω),

	Φ		( jω) = E +(R		( jω)*W	T −1		*
где						( jω)
		η,γ ,ξ	[	η,γ ,ξ	η,γ ,ξ		]

*Rη,γ ,ξ ( jω)*Wη,γ ,ξ ( jω T ;

Е– единичная матрица (m x m).

Так как Φη,γ,ξ ( jω) не зависти от пространственных координат, то

система управления пространственно-инвариантна, и таким образом, утверждение доказано.

1.1.7 Экспериментальное определение частотных характеристик нагревательной камеры

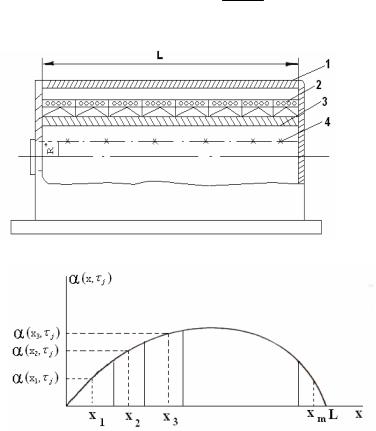
Рассмотрим определение частотных характеристик коаксиальной нагревательной камеры. Конструктивно нагревательная камера (см. рис.1.6) оформляется в виде коаксиально расположенных: охлаждаемого корпуса (1); секционного нагревателя (2) (число секций m); трубы (3); датчиков изменения температурного поля (4), которые находятся внутри камеры на радиусе R* (число датчиков n).

Длина камеры равна L. Оба конца камеры имеют постоянную температуру, равную нулю.

Управляющим воздействием (α(x,τ)) служит тепловой поток

секционного нагревателя.

Для частотного анализа объекта приложим управляющее воздействие в виде:

α ( x,τ ) = q * sin( ω *τ ) * sin( π L*η * x ), (1.59)

где q,ω,η- фиксированные числа.

Рисунок 1.6. Нагревательная камера

Рисунок 1.7. График управляющего воздействия

<<< < Предыдущая 1 23 / 213 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.03.201666.67 Кб9Biznes_plan.Docx
#
25.04.2019326.2 Кб2blablabla.docx
#
07.12.2018324.98 Кб36blablabla.docx
#
08.09.2019132.61 Кб1Blanki.doc
#
21.03.20161.19 Mб30book_holography_2009.pdf
#
21.03.20163.83 Mб14Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov.pdf
#
14.11.20191.28 Mб28BZhD_Laboratornaya_rabota_4.doc
#
21.04.2019536.06 Кб21C++ лекции.doc
#
21.03.2016358.65 Кб21C. Вводная лекция.pdf
#
21.03.2016534.94 Кб19C. Тема 1. Раздел 1.pdf
#
21.03.2016546.75 Кб18C. Тема 1. Раздел 10.pdf