Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov

.pdf

Скачиваний:

Добавлен:

21.03.2016

Размер:

3.83 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 215 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

θi (x, y,τ) - свободное движение по i-му (i =1, m) выходу системы.

В этом случае доказательство достаточного условия устойчивости аналогично приведенному выше.

Таким образом, для устойчивости пространственно-инвариантной системы достаточно, чтобы каждый контур был асимптотически устойчив.

1.2.2 Анализ устойчивости по дисперсионным соотношениям

Положим, что математическая модель замкнутой системы описывается дифференциальным уравнением вида /16/

∂2Q(x,t)+ a

∂Q(x,t)= b ∂2Q(x,t)

+ b ∂Q(x,t)

+ b Q(x,t)

∂t2

∂t

0 ∂x2

1 ∂x

где a0 ,a1,b0 ,b1,b2 - постоянные коэффициенты.

При этом будем полагать, что граничные условия однородны.

Решение уравнения будем искать в виде

Q(x,t)= exp(s t + s t),

где s, s - комплексные временная и пространственная частоты.

Подставляя Q(x, t)

в исходное уравнение и преобразуя, получим

дисперсионное уравнение

a0 s

+ a1 s = b0

+ b1

= λ

s + b2

или

(λ, s)= a

+ a s − λ = 0

− λ = 0 ,

s (λ, s)= b0 s

+ b1 s

где λ - собственные значения данной краевой задачи (спектр данной краевой задачи), формируемые граничными условиями.

Если корни дисперсионного уравнения, определяющего временной характер процесса, имеют отрицательные действительные части, то процесс устойчив.

Если среди всех корней найдется хотя бы один, у которого имеется положительная действительная часть, то система неустойчива.

Так как λ Λ, где Λ - бесконечное множество действительных чисел, то получим бесконечное множество корней дисперсионного уравнения.

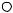
1.3 Особенности применения критерия Найквиста к пространственно-инвариантным системам

1.3.1 Обобщение критерия Найквиста на системы управления

Обобщение критерия Найквиста на системы управления, передаточная функция которых может быть представлена отношением аналитических целых функций, основывается на использовании принципа аргумента для аналитических функций.

Согласно /11,19/, можно записать:

1	σ∫	Φ р (s)ds		1	arg (1	+ Φ p (s))		= m1 − m 2 ,

			=				σ
2π j		1 + Φ р (s)		2π j

где Φ p (s) - передаточная функция разомкнутой системы; m1 - число нулей функции 1+ Φ p (s), лежащих в контуре σ;

m2 - число полюсов функции 1+ Φ p (s) , лежащих в контуре σ .

В /11/ приведено доказательство критерия Найквиста для систем управления, передаточные функции которых (Φ p (s)) могут быть

представлены отношением аналитических целых функций. При отображении контура σ на всю правую полуплоскость s показано, что для устойчивости системы необходимо и достаточно, чтобы m1 − m2 = 0 .

Основная трудность применения критерия Найквиста к системам управления, передаточные функции которых представлены в виде отношения аналитически целых функций, связана с необходимостью вычисления разности m1 − m2 , которая может оказаться разностью двух

бесконечно больших чисел.

В /19/ приведены условия, которым должна удовлетворять передаточная функция разомкнутой системы, представленная в виде отношения аналитически целых функций. Эти условия заключаются в следующем: а) lim Φ p (s)= const и б) внутри контура интегрирования (σ )

s→∞

передаточная функция должна быть мероморфной. Таким образом, необходимо исследовать в каждом конкретном случае передаточную функцию разомкнутой системы.

В соответствии с п.1.3, пространственно-инвариантную систему управления можно представить как совокупность независимых контуров управления по каждой пространственной моде входного воздействия. В п.2.1 показано, что если каждый контур асимптотически устойчив, то и система управления в целом устойчива.

Передаточная функция по каждому контуру пространственноинвариантной системы может быть представлена отношением бесконечных полиномов.

Для определения возможности применения критерия Найквиста к каждому контуру системы управления необходимо, провести анализ передаточной функции каждого из контуров.

Пример 1.

Исследуем передаточную функцию процесса распространения тепла в цилиндрическом стержне.

Рассмотрим применение частотного критерия Найквиста к анализу устойчивости в каждом контуре системы управления процессом распространения тепла в цилиндре конечных размеров, управляющее воздействие, на который распределено по границе.

Согласно (1.29), передаточная функция объекта по η-й моде входного воздействия (η =1,∞)может быть представлена в виде отношения функций Бесселя:


				J
				J	0,η R, s
	W		(s)=			,
	W		(s)=			,
	0,η			J0,η (R, s)
				J0,η (R, s)
где
где	R, R - заданные числа.	в виде J0,η (jz), (η =						), рассмотрим
Представляя функцию J0,η (R, s)
Представляя функцию J0,η (R, s)							1,∞

поведение функции на контуре интегрирования бесконечно большого радиуса.

Функция J0,η (jz) при бесконечно больших значениях аргумента z , согласно /112/, может быть представлена в виде следующего соотношения:

																		2
J	0,η	(jz)=	1			exp(z) 1		+			1			+		1 3					+K			,		arg z				≤		π , (η =1,∞).
J		(jz)=				exp(z) 1		+						+							+K			,		arg z				≤		π , (η =1,∞).
			(2π z)	1	2				1!8z									2														2
				1														2
																2! (8z)
Найдем предел:


																							1				1 3		2
																			1		+		1		+		1 3					+K
																			1		+				+						2	+K
																															2		,	(1.70)
							(2π z				)12											1!8 zη					2! 8 zη						,	(1.70)
							(2π z				)12				exp(		zη )
			lim W0,η (s)= lim							η
			lim W0,η (s)= lim									1																	2
			s→∞			s→∞						1	2										1				1	3	2
													2							1+			1		+		1	3				+K

																															2
							2π zη																1!8zη								2
																							1!8zη				2! (8zη )

(η =1,∞),

где, согласно /39/, значения аргументов zη , zη к функции могут быть найдены из следующих соотношений:

, (η =1,∞),

zη =

+ψη

+ψ 2

R , (η =1,

∞)

, (η =1,∞).

z = R− R

+ψη

zη (η =1,∞)

(1.71)

Преобразуя (2.8), получим



										1				1	3	2
								1	+	1	+			1	3			+K
								1	+		+					2		+K
												2!				2
			1	2			12		1!8 zη			2!		8 zη
				2			12
		R			s
lim W0,η (s)= lim					exp	+ψη2	R− R												,
lim W0,η (s)= lim					exp	+ψη2	R− R												,
s→∞																2
s→∞	s→∞				a					1				1 3		2
										1				1 3
	R							1+			+						+K
	R							1+		1!8zη	+					2	+K
										1!8zη			2! (8zη )

(η =1,∞).

Так как из физических условий R < R , то

lim W		(s)= 0 , (η =		).
	0,η		1,∞
s→∞

Предположим, что передаточная функция регулятора по η-й (η =1,∞)моде входного воздействия равна Kη (η =1,∞)( Kη - заданные числа).

В этом случае характеристический полином разомкнутой системы η-го контура имеет вид:

J0,η (jzη )= 0 , (η =1,∞).

	~
Рассмотрим отображение правой полуплоскости S на плоскость Γ = j zη .
Положим
S = M1(cos(ϕ1 )+ j sin(ϕ1 )),	(1.72)

где M1 - модуль комплексного числа S;

ϕ1 - фаза комплексного числа S (см. рис. 2.2). Подставляя (1.72) в (1.71), получим,


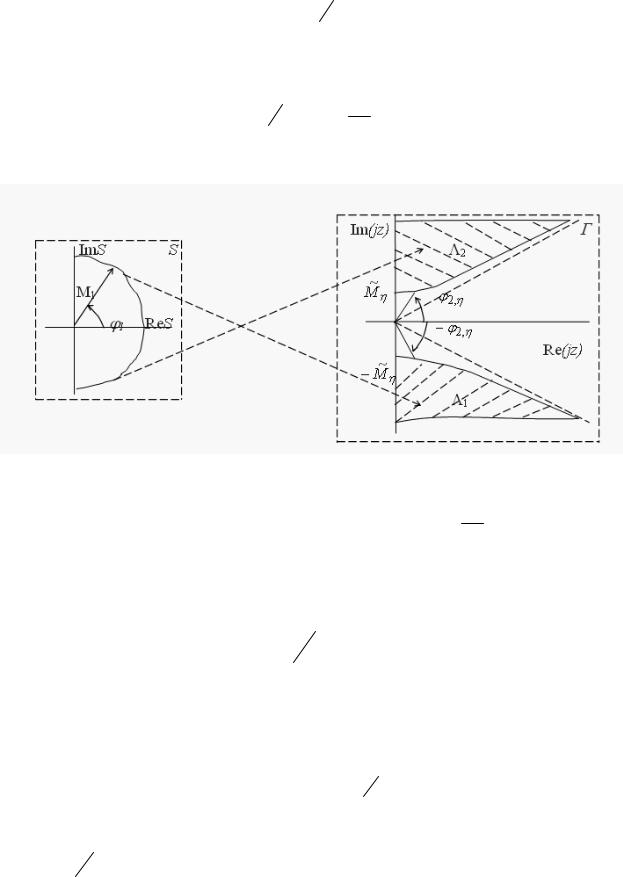
	j zη = j [M 2 (cos(ϕ1 )+ j sin(ϕ1 ))+ψη2 ]12 R , (η =					),	(1.73)
	j zη = j [M 2 (cos(ϕ1 )+ j sin(ϕ1 ))+ψη2 ]12 R , (η =				1,∞	),	(1.73)
где	M 2	=	M1	.
где	M 2	=		.
			a

Преобразуя (1.73), придем к следующему результату: j zη = [− M 2 (cos(ϕ1 )+ j sin(ϕ1 ))−ψη2 ]12 R , (η =1,∞).

Рис. 1.19. Отображение областей

Для удобства рассмотрения комплексных чисел j zη (η =1,∞)на

комплексной плоскости Γ (см. рис. 1.19) представим комплексное число j zη в показательной форме:

jzη = Aη exp(jϕ2,η ), (η =

1,∞

где

2,η

= ϕ3,η

;

(1.74)

− M 2 sin(ϕ1 )

;

ϕ3,η = arctg

−

cos(ϕ

)−ψ

(1.75)

14 ; (η =

Aη = R (M

2 sin(ϕ1 ))2

+ (M 2

cos(ϕ1 )−ψη2 )2

1,∞

(1.76)

= π

При ϕ

значение ϕ

2,η

, согласно (1.74), (1.75), определяется из

следующего соотношения:

J0,η (R, S )

J0,η (jzη ),

arctg

− M 2

, (η =

2,η

1,∞

−ψη

Найдем предел

− M

= −π

, (η =

lim

arctg

2,η

1,∞

− a ψ 2

M1 →∞

= M1 →∞ 2

Аналогично можно показать, что при ϕ1 = −

π и M1, стремящемуся к ∞,

π .

значение ϕ2,η стремиться к

На рис. 1.19. показано отображение правовой полуплоскости S на

плоскость Γ. Это отображение получается в виде векторов Λ1 и Λ2.

Значение ~ равно ψ R .

Mη η

Исследования, проведенные в /39/, показывают, что функции

(η =1,∞)в секторах Λ1 и Λ2 не имеют нулей, а, следовательно, функция не имеет нулей, лежащих в правой полуплоскости S. Это

отражает известное свойство устойчивости тепловых процессов.


Аналогично, исследуя функцию J0,η R, S , (η =1,				∞), можно показать, что

она также не имеет нулей, лежащих в правой полуплоскости S. Изложенная методика позволяет судить о нулях и полюсах передаточной функции по каждому контуру управления одномерным температурным полем.

Полученные результаты для передаточной функции по каждому контуру управления температурным полем цилиндра говорят о том, что передаточная функция не имеет нулей и полюсов, лежащих в правой полуплоскости S, является мероморфной функцией и на контуре интегрирования бесконечно большого радиуса функция не имеет особенностей. Следовательно, критерий Найквиста применим к каждому контуру системы управления температурным полем цилиндра конечных размеров.

Пример 2.

Исследуем передаточную функцию процесса распространения тепла в пластине.

Докажем применимость критерия Найквиста к анализу устойчивости системы управления температурным полем пластины конечных размеров.

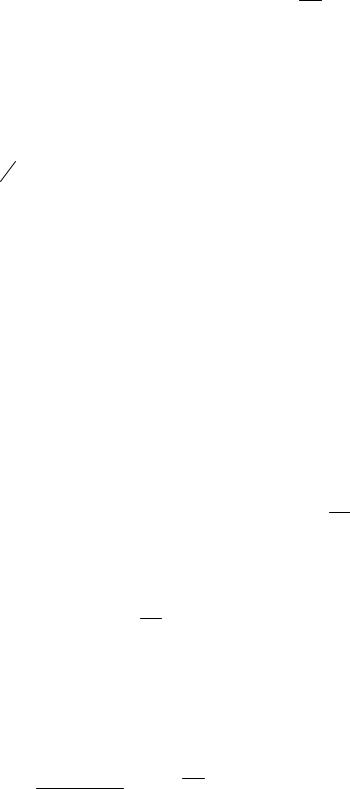
Согласно (1.15), передаточная функция объекта по η,γ (η,γ =1,∞)моде

входного воздействия при

z = z z < zL

имеет вид:

− βη,γ

exp βη,

+ exp

(s)=

γ =

(1.77)

0,η,γ

∞

exp

(βη,γ

zL )+ exp(− βη,γ

zL )

, ( ,

где βη,γ

, (η,γ =1,∞);

+ψη

+ϕγ

a, z, zL - заданные числа.

Рассмотрим поведение функции на контуре интегрирования бесконечно большого радиуса. Для этого найдем предел:

lim W0,η,γ (s)=

S →∞



	β		− z
lim exp	β	z	− z	L
S →∞		η,γ		L


		− 2βη,γ
1	+ exp	− 2βη,γ	z
				,	(η,γ =1,∞). (1.78)
(1+ exp(− 2βη,γ				,	(η,γ =1,∞). (1.78)
(1+ exp(− 2βη,γ			zL ))

Преобразуя (1.78), получим:



lim	W			−	β
lim	W	(s)= lim exp		−	β	η,γ	z	L		− z
S →∞	0,η,γ	S →∞				η,γ		L



Так как из физических условий											<
Так как из физических условий										z	<
			lim W		0,η,γ		(s)		= 0 ,
		S →∞			0,η,γ


				− 2βη,γ
	1	+ exp		− 2βη,γ	z
						,
	(1+ exp(− 2βη,γ					,
	(1+ exp(− 2βη,γ				zL ))



zL , а			> 0 , то
zL , а		z	> 0 , то

(η,γ =1,∞).

(1.79)

Передаточная функция (1.77) может быть представлена в виде:

Сh βη,γ z

W0,η,γ (s)= Сh(βη,γ zL ), (η,γ =1,∞).

Как известно /39/, у функции Ch(~z ), где ~z – комплексное число, нули располагаются на мнимой оси.

В рассматриваемом случае

~		s	2	~	12	zL .
z	= βη,γ	zL =	+ψη	+ϕγ

		a

При Re(s)≥ 0 функции Ch(βη,γ zL ), (η,γ =1,∞)не имеют нулей, лежащих в правой полуплоскости S. Аналогично можно показать, что функции


		, (η,γ =1,∞)не имеют нулей, лежащих в правой полуплоскости S.

Ch	βη,γ z


Так как функции Ch	βη,γ z , Ch(βη,γ zL ) регулярны, не имеют нулей,

лежащих в правой полуплоскости S, и выполняется условие (1.78), то модифицированный критерий Найквиста применим к каждому контуру системы управления (при этом полагаем, что передаточная функция регулятора по каждой пространственной моде может быть представлена в виде соотношения конечных полиномов).

1.3.2 Критерий устойчивости Найквиста для пространственноинвариантных систем со скалярным входным воздействием

Пусть имеется передаточная функция разомкнутой пространственноинвариантной системы управления по каждой моде входного воздействия:

(s)=

Πη,γ ,ξ (s)

(η,γ =

; ξ =

(1.80)

1,∞

1,4

η,γ ,ξ

Μη,γ ,ξ (s)

(s) - аналитические целые функции, обладающие

где Πη

,γ ,ξ (s) и Μη,γ ,ξ

свойствами, рассмотренными в п.2.3.

Представим выражение (1.80) в виде:

~ ~

Π(G,s)

W (G, s)=

~ ~

(1.81)

Μ(G, s)

Gн ≤ G

≤ Gк,

~ ~

~(η γ ξ) Gн Gк

где G , , - дискретная функция с областью изменения от до (в

общем случае ~ → ∞

Gк ).

Работать с бесконечным набором передаточных функций (1.81) не всегда

удобно. Перейдем от набора функций (1.81) к функциональной

зависимости (G,s). Для этого заменим G непрерывной функцией G с

[ = ~ ∞]

областью определения Gн Gн, . В этом случае, при изменении G до

н ∞, охватятся все дискретные значения функции ~ , определенные для

G G

любых значений η,γ [1,∞]; ξ [1,4]. Таким образом, функция W(G,s) может быть представлена в виде следующего соотношения:

~	,	(1.82)
W (G, s)= Π(G, s)~	,	(1.82)
Μ(G, s)

Gн ≤ G ≤ ∞.

Функцию G назовем обобщенной координатой.

Так, например, с использованием обобщенной координаты, передаточная функция (1.81) может быть записана в виде:

exp

β(G) z

+ exp

− β(G) z

W (G, s)=

, G

≤ G ≤ ∞,

exp(β(G) zL )+ exp(− β(G) zL )

где β(G)= (G + s

) 2 , G

=ψ

= G

+ϕ

Для частотного анализа объекта положим в (1.82) s=jω.

При изменении значения ω от 0 до ∞, а значения G от Gн до ∞, вектор W(G,jω) в пространстве Re(W), Im(W), G опишет поверхность, которую назовем пространственным годографом (см. рис. 1.20). Для определения

частотной характеристики объекта, по заданной , , пространственной

η γ ξ

гармонической составляющей входного воздействия, необходимо рассечь пространственный годограф плоскостью Γ, параллельной плоскости Γ1 и проходящей через точку с координатами:

~
Re(W)=0, Im(W),=0, G = G η,γ		,ξ .

След пересечения плоскости Γ и пространственного годографа будет представлять искомую частотную характеристику.

Аналогично может быть построен пространственный годограф для разомкнутой пространственно-инвариантной системы управления. Таким образом, пространственный годограф описывает частотные характеристики всей совокупности контуров разомкнутой пространственно-инвариантной системы управления.

Рис. 1.20. Пространственный годограф.

Введенный пространственный годограф и утверждение 1 п. 2.1. позволяют дать следующую графическую интерпретацию критерия Найквиста-

если передаточная функция разомкнутой системы не имеет полюсов, лежащих в правой полуплоскости S, тогда для устойчивости замкнутой системы достаточно, чтобы пространственный годограф разомкнутой системы не охватывал линию L {Im(W ) = 0; Re(W ) = −1;G}.

В этом случае частотная характеристика каждого η,γ ,ξ контура системы управления не охватит точку с координатами Im(W ) = 0; Re(W ) = −1.

Следовательно, каждый контур системы управления будет устойчив, а в силу п.2.1 будет устойчива и вся система.

Для анализа устойчивости по критерию Найквиста можно строить не пространственный годограф разомкнутой системы, а логарифмическую амплитудную частотную поверхность и фазовую частотную поверхность. На рис. 1.2.1 пространственный годограф представлен в виде логарифмической амплитудной (рис. 1.21,а) и фазовой (рис. 1.21,г) частотных поверхностей.

На графиках (рис. 1.21,а) на оси L отложено значение 20lgW (G, jω), а на рис. 1.21,г по оси ϕ отложено значение arctg Im(W (G, jω))Re(W (G, jω)) .

Рис. 1.22. Частотные поверхности

<<< < Предыдущая 1 2 3 45 / 215 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.03.201666.67 Кб9Biznes_plan.Docx
#
25.04.2019326.2 Кб2blablabla.docx
#
07.12.2018324.98 Кб36blablabla.docx
#
08.09.2019132.61 Кб1Blanki.doc
#
21.03.20161.19 Mб30book_holography_2009.pdf
#
21.03.20163.83 Mб14Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov.pdf
#
14.11.20191.28 Mб28BZhD_Laboratornaya_rabota_4.doc
#
21.04.2019536.06 Кб21C++ лекции.doc
#
21.03.2016358.65 Кб21C. Вводная лекция.pdf
#
21.03.2016534.94 Кб19C. Тема 1. Раздел 1.pdf
#
21.03.2016546.75 Кб18C. Тема 1. Раздел 10.pdf