Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov

.pdf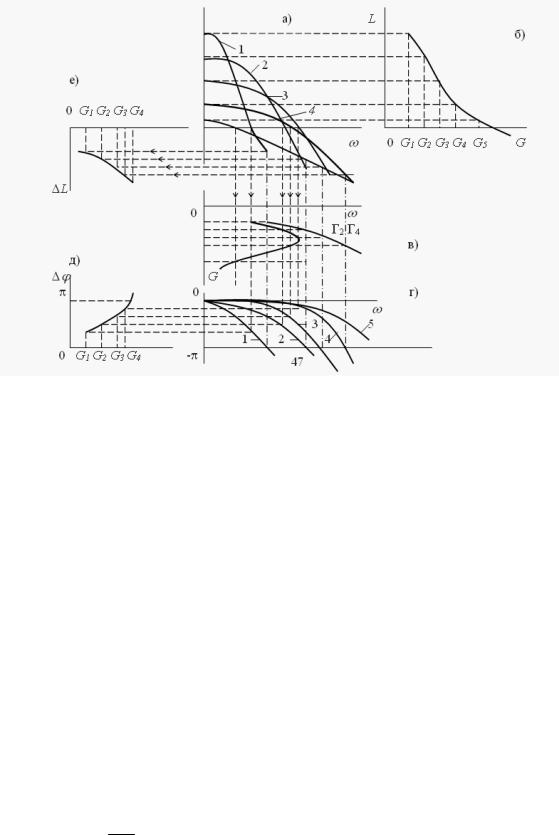

Скачиваний:

Добавлен:

21.03.2016

Размер:

3.83 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 216 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Рис. 1.23. Построение частотных характеристик.

След пересечения логарифмической амплитудной частотной поверхности с

плоскостью Γ3 назовем статической кривой (рис. 1.21,б). По статической

кривой для каждого η,γ ,ξ контура системы управления может быть определен статический коэффициент передачи.

След пересечения плоскости Γ2 (L=0) и логарифмической амплитудной частотной поверхности назовем линией среза модуля (рис. 1.21,а). След пересечения фазовой частотной поверхности с плоскостью Γ4

назовем линией среза фазы.

Интерпретация критерия Найквиста при помощи частотных поверхностей заключается в следующем.

Если передаточная функция разомкнутой системы не имеет полюсов, лежащих в правой полуплоскости S ,то для устойчивости замкнутой системы достаточно, чтобы при совмещении плоскостей Γ2 и Γ4 линия среза модуля не имела с областью Λ, включая и границу (см. рис.

1.21,в), общих точек.

Для оценки устойчивости и статики замкнутой системы достаточно построить линии среза модуля и фазы и статическую кривую.

При решении практических задач выбирается некоторое конечное число значений Gi (i =1,m ), для которых (см. рис. 1.22,а и 1.22,г) строятся

логарифмические амплитудные и фазовые частотные характеристики и статическая кривая (рис. 1.22,б). По полученным характеристикам и статической кривой строятся линии среза модуля и фазы (рис. 1.22,в).

РАЗДЕЛ №2. РАСПРЕДЕЛЕННЫЕ ЗВЕНЬЯ И БЛОКИ

2.1 Основные понятия и описания распределенных звеньев

2.1.1 Распределенные звенья

Поскольку процесс регулирования не зависит от физической природы регулируемой величины, то среди всех распределенных звеньев, составляющих систему регулирования и обладающих свойством пространственной инвариантности, можно выделить следующие элементарные звенья.

1. Пространственно-усилительное звено

Положим, что имеется распределенное звено, у которого определено входное воздействие и функция выхода.

Пусть заданы изображения по Лапласу при нулевых начальных условиях входного воздействия (α(x, y,s)) и функции выхода (U (x, y, s)),

которые связаны соотношением:

U (x, y, s)= E	n1 −1	α(x, y, s)−	1	2 α(x, y,s)	,	(2.1)
U (x, y, s)= E	n	α(x, y, s)−	n	2 α(x, y,s)	,	(2.1)
1	n		n
	1		1

где E1 - заданное число (общий коэффициент усиления); x, y – пространственные координаты;

2 - лапласиан; s -оператор Лапласа; n1 – весовой коэффициент ( n1 ≥1):

при	n1=1	U (x, y, s)= −E 2α(x, y, s);	при	n → ∞
U (x, y, s)→ E1 α(x, y, s).		1		1
U (x, y, s)→ E1 α(x, y, s).

Передаточную функцию распределенного звена, определяемую отношением U (x, y, s) к α(x, y, s) , можно записать следующим образом:

W	(x, y)= E	n1 −1	−	1	2	.	(2.2)
W	(x, y)= E	n	−	n	2	.	(2.2)
1	1	n		n
		1		1

Распределенное звено, передаточная функция которого может быть представлена в виде (2.2), назовем пространственно-усилительным. Для определения статических характеристик пространственно-

усилительного звена представим входное воздействие в виде ряда Фурье

∞	4
α(x, y, s)= ∑ ∑Cη,γ ,ξ (s) Bη,γ ,ξ (x, y)		(2.3)

η,γ =1ξ =1

(где значения функции Bη,γ ,ξ (x, y) определяются в соответствии с (1.17)) и определим функцию выхода (U (x, y, s)).

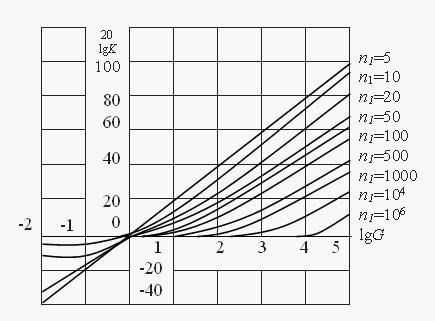
Рис. 2.1. Графики K.

Подставляя (2.3) в (2.1), получим:

	n			−1		1	∂2α			∂2α
U (x, y, s) = E		1			α −			2	+		2	.	(2.4)
						n
1			n				∂x			∂y
				1		1

Преобразуя (2.4), придем к следующему результату:

∞ 4

U (x, y, s) = ∑ ∑E1

η,γ =1ξ =1

n1 −1			1	2	~2
		+		(ψη	+ϕγ	)	Сη,γ ,ξ (s) Bη,γ ,ξ (x, y).
	n	+	n	(ψη	+ϕγ	)	Сη,γ ,ξ (s) Bη,γ ,ξ (x, y).
	1		1

(2.5)

Коэффициент усиления пространственно-усилительного звена по каждой составляющей ряда входного воздействия имеет вид:

		n1 − 1			1	2	~ 2
Kη,γ ,ξ	= E1			+		(ψη	+ ϕγ	)	,	(2.6)
Kη,γ ,ξ	= E1		n	+	n	(ψη	+ ϕγ	)	,	(2.6)
			1		1

(η,γ =1,∞; ξ =1,4).

Из (2.6) следует, что рассматриваемое звено обладает свойством пространственной инвариантности.

Представим (2.6) в следующей форме:

n −1

= E

(2.7)

η,γ ,ξ

где

=ψη

+ϕγ - дискретная функция (η,γ =1,∞). Значения функции

зависят не только от η, γ , но и от xL ,

yL (см. 1.17).

Из (2.7) следует, что коэффициент усиления не зависит от ξ. Таким образом, передаточная функция пространственно-усилительного звена может быть представлена бесконечной совокупностью коэффициентов усиления (2.7). Работать с бесконечным набором функций (2.7) не всегда

удобно. Перейдем, как в п.2, от набора функций (2.7) к функциональной

зависимости K(G). Для этого заменим G непрерывной функцией G с областью определения

[0,∞]. В этом случае, при изменении G от 0 до ∞, охватятся все дискретные

значения G .

Выражение (2.7), с учетом изложенного выше, может быть записано в виде:

n1 −1			1
K (G) = E1		+		G	, 0 ≤ G ≤ ∞ .
K (G) = E1	n	+	n	G	, 0 ≤ G ≤ ∞ .
	1		1

На рис. 2.1 приведены графики изменения статического коэффициента усиления пространственно-усилительного звена (при этом полагалось E1=1).

Передаточные функции распределенных звеньев, рассмотренные ниже, получены аналогично передаточной функции пространственноусилительного звена.

2. Идеальное пространственно-дифференцирущее звено

Передаточная функция такого звена имеет вид:

W2 (x, y, s)= E2	n	2	−1		1	2	s ,
				−				(2.9)
		n2			n2

где Е2 – заданный коэффициент; n2 – весовой множитель (n2 ≥1).

Для определения динамических характеристик идеального пространственно-дифференцирующего звена подадим на вход воздействие (2.3) и определим функцию выхода

−1

∂2a

U (x, y, s) = E2

а −

s .

(2.10)

∂x

∂y

Преобразуя (2.10), получим:

∞ 4

−1

U (x, y, s) = ∑ ∑E2

(ψη

+ϕγ

)

s Сη,γ ,ξ (s) Bη,γ ,ξ (x, y).

η,γ =1ξ =1

(2.11)

Передаточная функция по каждой составляющей ряда входного воздействия может быть записана в виде:

	n2 −1			1	2	~2
Wη,γ ,ξ (s) = E2			+		(ψη	+ϕγ	)	s ,	(2.12)
		n2		n2

(η,γ =1,∞; ξ =1,4).

Перейдем от бесконечного набора функций (2.12), к функциональной зависимости W2(G,s)

W	(G, s) = E		n2 −1	+	1	G	s ,	(2.13)
		2
2			n2		n2

0 ≤ G ≤ ∞ .

На рис. 2.2. показаны амплитудная и фазовая частотные поверхности идеального пространственно-дифференцирующего звена.

Постоянная времени рассматриваемого звена, согласно (2.13), определяется из следующего соотношения

	n2 −1			1
T = E2			+		G	, 0 ≤ G ≤ ∞ .	(2.14)
		n2		n2

Рис. 2.2. Частотные поверхности.

Как известно, частота среза связана с постоянной времени следующим соотношением

ωc = T1 .

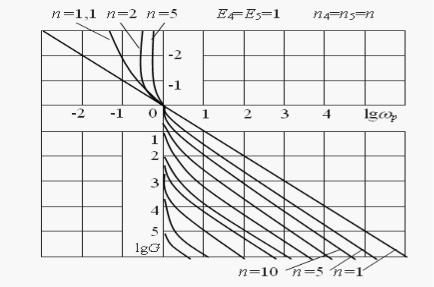
На рис. 2.3. приведены графики изменения частоты среза в зависимости от G и n2 (где n=n2). При построении графиков полагалось

E2=1.

	3. Пространственно-форсирующее звено
Передаточная функция этого звена имеет вид:
	n3 −1		1	2
W3	(x, y, s) = E3	−			s +1,	(2.15)
			n3
	n3

где E3 – заданное число; n3 – весовой коэффициент (n3 ≥1).

Если на вход пространственно-форсирующего звена подать воздействие (2.3), на выходе получим

∞	4	n3 −1		1		2	~2
U(x, y,s) = ∑ ∑ E3				+		(ψη	+ϕγ	)	s Сη,γ ,ξ (s)
U(x, y,s) = ∑ ∑ E3			n	+	n	(ψη	+ϕγ	)	s Сη,γ ,ξ (s)
			3	3
η,γ =1ξ=1
Bη,γ ,ξ (x, y)+ Сη,γ ,ξ (s) Bη,γ ,ξ (x, y)}.
		(2.16)

Рис. 2.3. Графики частоты среза.

Преобразуя (2.16) с учетом (2.3), получим:

∞	4	n3 − 1			1	2	~ 2
U ( x, y, s) = ∑ ∑ E3				+		(ψη	+ ϕγ	)	s + 1	Сη,γ ,ξ (s )
U ( x, y, s) = ∑ ∑ E3			n3	+	n3	(ψη	+ ϕγ	)	s + 1	Сη,γ ,ξ (s )
			n3		n3
η,γ =1ξ =1

Bη,γ ,ξ (x, y ).

Передаточная функция звена, записанная с использованием обобщенной координаты, имеет вид:

W (G, s) = E		n3 −1	+	1	G	s +1, (2.17)
W (G, s) = E	3	n	+	n	G	s +1, (2.17)
3	3	n		n
		3		3

0 ≤ G ≤ ∞ .

На рис. 2.4 приведены амплитудная и фазовая частотные поверхности пространственно-форсирующего звена. Графики частот среза звена показаны на рис. 2.3 (где n=n3).

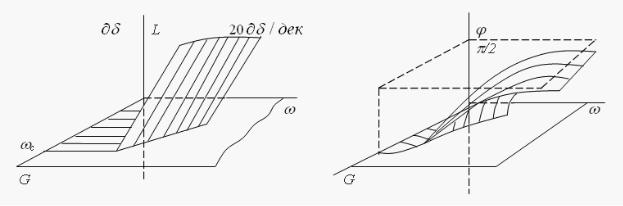
Рис. 2.4. Частотные поверхности

4. Идеальное пространственно-интегрирующее звено

Передаточная функция идеального пространственно-интегрирующего звена имеет вид:

W4 (x, y, s) = E4	n4 −1			1	2	1	,	(2.18)
			−
		n4		n4		s

где E4 – заданное число;

n4 – весовой коэффициент (n4 ≥1).

Если на вход звена подать воздействие (2.3), на выходе получим функцию

−1

∂2a

U (x, y, s) = E4

−

(2.19)

∂x

∂y

Преобразуя (2.19), перейдем к следующему результату:

∞ 4

n4 −1

U (x, y, s) = ∑ ∑E4

(ψη +

ϕγ

)

Cη,γ ,ξ (s) Bη,γ ,ξ (x, y).

η,γ =1ξ =1

Передаточная функция звена, записанная с обобщенной координаты (G), имеет вид:

W (G, s)=E		n4 −1	+	1	G	1 ,

4	4	n4				s
				n4

0 ≤ G ≤ ∞ .

использованием

(2.20)

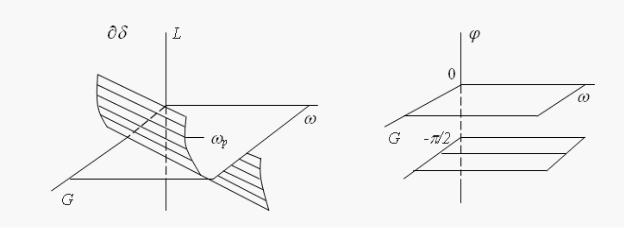
Рис. 2.5. Частотные поверхности.

Частота среза идеального пространственно-интегрирующего звена определяется из следующего соотношения:

	n4 −1		1

		+		G	, 0	≤ G ≤ ∞ .
ω p = E4	n4		n4

На рис. 2.5 показаны амплитудная и фазовая частотные поверхности пространственно-интегрирующего звена. Графики частоты среза приведены на рис. 2.6 (где n=n4).

5. Пространственно-изодромное звено

Передаточная функция пространственно-изодромного звена имеет вид:

−1

(x, y, s)= E 5

−

+1,

(2.21)

где E5 – заданное число;

n5 – весовой коэффициент (n5 ≥1).

Подавая на вход звена воздействие (2.3), на выходе получим:

n −1

∂2a

U (x, y, s) = E

α −

+α .

(2.22)

∂x

∂y

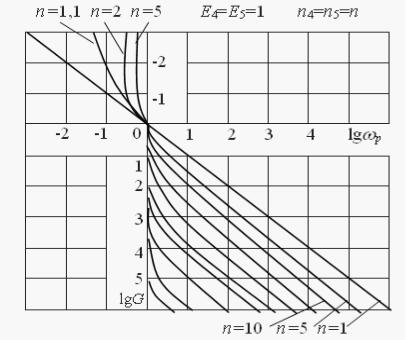
Рис. 2.6. Графики частоты среза.

Преобразуя (2.22) с учетом (2.3), придем к следующему результату:

∞

n5 −1

U (x, y,s) = ∑ ∑

(ψη

+ϕγ

)

η,γ =1ξ =1

Cη,γ ,ξ (s) Bη,γ ,ξ (x, y).

Передаточная функция пространственно-изодромного звена, записанная с использованием обобщенной координаты (G), может быть представлена в виде следующего соотношения:

На рис. 2.7 показаны амплитудная и фазовая частотные поверхности пространственно-изодромного звена. График частот среза рассматриваемого звена приведен на рис. 2.6 (где n=n5).

W (G, s)=E			n5 −1	+	1	G	1	+1,
W (G, s)=E	5		n	+	n	G	s	+1,
5	5		n		n		s
			5		5
		0	≤ G ≤ ∞ .

<<< < Предыдущая 1 2 3 4 56 / 216 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.03.201666.67 Кб9Biznes_plan.Docx
#
25.04.2019326.2 Кб2blablabla.docx
#
07.12.2018324.98 Кб35blablabla.docx
#
08.09.2019132.61 Кб1Blanki.doc
#
21.03.20161.19 Mб30book_holography_2009.pdf
#
21.03.20163.83 Mб14Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov.pdf
#
14.11.20191.28 Mб27BZhD_Laboratornaya_rabota_4.doc
#
21.04.2019536.06 Кб21C++ лекции.doc
#
21.03.2016358.65 Кб21C. Вводная лекция.pdf
#
21.03.2016534.94 Кб18C. Тема 1. Раздел 1.pdf
#
21.03.2016546.75 Кб18C. Тема 1. Раздел 10.pdf