Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov

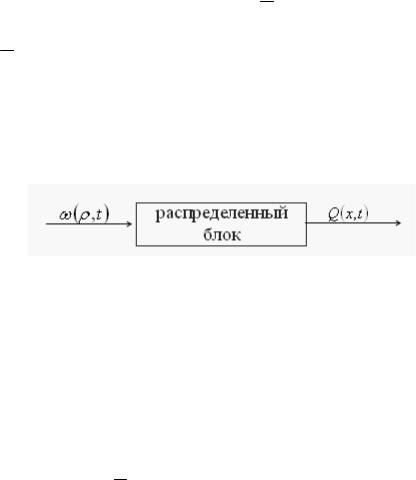
Q (x, t )= ∫t ∫G (x, t, ρ,τ ) ω (ρ,τ )dρ dτ ,

t0 D1

где G(x,t, ρ,τ ) - функция Грина (импульсная переходная функция). Полагая, что на вход распределенного блока поступило единичное

получим:

t

Q(x,t)= ∫ ∫G(x,t, ρ,τ ) δ (ρ − ρ0 ) δ (τ −τ0 )dρdτ = G(x,t, ρ0 ,τ0 ) t0 D

Интегральное соотношение для функции выхода может быть задано в виде:

Q(x,t)= G(x,t, ρ,τ ) ω(ρ,τ ),

где символ означает интегрирование двух связанных с этим символом функций по параметрам ρ D1 и τ .

Если параметры распределенного объекта не зависят от времени, то соответствующий ему распределенный блок будем называть стационарным.

Рисунок 1.2. Распределенный блок.

Импульсная переходная функция такого блока может быть записана в виде:

G(x,t, ρ,τ )= G(x, ρ,t −τ ).

Стационарные распределенные блоки удобно записывать в терминах преобразования Лапласа сигнала f (x,t) и функции Грина G(x, ρ,t)

f (x, s)= ∞∫exp(− st) f (x,t)dt ,

0

10

∞

W (x, ρ, s)= ∫exp(− st)G(x, ρ,t)dt ,

0

где W (x, ρ, s) называется передаточной функцией рассматриваемого

распределенного блока.

В терминах преобразования Лапласа по времени распределенный блок может быть описан соотношением:

Q(x, s)= ∫W (x, ρ, s)ω(ρ, s)dρ ,

D1

где Q(x,s), ω(ρ, s) - преобразования по Лапласу функции Q(x,t), ω(ξ,τ)

соответственно.

В /7/ приведены характеристики большого класса линейных систем с распределенными параметрами, описываемых уравнениями математической физики.

Пример.

Приведем импульсную переходную функцию G и передаточную функцию W для объекта, математическая модель которого представлена в виде (/14/, стр. 157):

11

Рассмотрим параллельное соединение n распределенных блоков (см. рисунок 1.3).

В этом случае G(x, ρ,t,τ )= ∑n Gi (x, ρ,t,τ ), i =1

где G(x, ρ,t,τ ) - импульсная переходная функция n – параллельно соединенных блоков.

Рисунок 1.3. Параллельное соединение.

Передаточная функция рассматриваемого соединения может быть записана в виде:

W(x, ρ, s)= ∑n Wi (x, ρ, s).

i=1

Аналогично могут быть записаны импульсная переходная функция и передаточная функция последовательно соединенных блоков (см. рис. 1.4.).

G(x, ρ,t,τ )= Gn (x, ρ,t,τ ) Gn−1(x, ρ,t,τ ) K G1(x, ρ,t,τ )

Передаточная функция последовательного соединения блоков имеет

вид:

W (x, ρ, s)= ∏1 Wi (x, ρ, s),

i=n

где - означает интегрирование двух связанных с этим символом функций по области, которой принадлежат две пространственные переменные.

12

Следует отметить, что такое представление распределенных объектов и систем оказалось удобным при моделировании.

Известно, что численное моделирование распределенных объектов, путем конечно-разностного представления частных производных сопряжено с тем, что шаг интегрирования во времени связан с параметрами дискретизации по пространственным переменным. Увеличение шага во времени, от некоторого порогового, приводит к неустойчивости вычислительной схемы. Поэтому, при таком моделировании, требуются большие затраты машинного времени.

Рисунок 1.4. Последовательное соединение.

Использование, при моделировании, структурного представления распределенных систем (с использованием функций Грина) позволяет снять ограничение на шаг интегрирования во времени.

1.1.3 Модальное представление распределенных объектов

Рассмотрим распределенные объекты, математические модели которых допускают разложение по собственным вектор-функциям оператора объекта.

Используя такое разложение, передаточная функция распределенного объекта может быть представлена совокупностью передаточных функций по пространственным модам.

Пример.

Положим, что имеется пластина конечных размеров, в которой осуществляется процесс распространения тепла. Математическая модель объекта описывается уравнением:

0<x<xL, 0<y< yL, 0<z< zL,

13

где T (x, y, z,τ) - фазовая переменная; x, y, z, - пространственные

координаты; а – заданный коэффициент; xL, yL, zL – заданные числа. Граничные и начальные условия для уравнения (1.2) имеют вид:

граничные условия (1.3), входное воздействие может быть представлено в виде:

Найдем реакцию объекта на каждую составляющую ряда (1.7). Эту реакцию будем искать в виде:

Tη,γ (x, y, z,τ)= Hη,γ (z,τ) sin(ψη x) sin(ϕ~γ y), (1.8)

Подставляя (1.8) в уравнение (1.2) и преобразуя, придем к следующему результату:

(η,γ =1,∞).

Преобразуем (1.9) по Лапласу при нулевых начальных условиях:

(η,γ =1,∞),

где Hη,γ (z, s) - изображение по Лапласу функции Hη,γ (z,τ) при нулевых начальных условиях (η, γ = 1, ∞).

14

Решение уравнения (1.10) можно представить в виде:

(η,γ =1,∞),

где Сη,γ (s) - изображение по Лапласу функции Cη,γ (τ) при нулевых начальных условиях (η,γ =1,∞).

Рассматривая совместно (1.11), (1.12), (1.13), с учетом (1.8), получим:

(1.14)

где Tη,γ (x, y, z, s) - преобразованная по Лапласу функция Tη,γ (x, y, z,τ ).

Передаточная функция объекта по η,γ (η,γ =1,∞) моде входного воздействия имеет вид:

(1.15)

(η,γ =1,∞).

Таким образом, рассматриваемый распределенный объект может быть представлен в виде совокупности передаточных функций W0,η,γ (s)

(η,γ =1,∞).

15

где Tμ, i,η, γ , ξ (x, y, z, jω) - решение системы уравнений (1.1) в

квазистационарном режиме по i-ой (i =1,n) фазовой переменной и входном воздействии

для i-ой переменной (i =1,n) по η,γ,ξ −ой составляющей (η,γ =1,∞; ξ =1,4) μ −го входного воздействия (μ =1,m) называется функция Wμ,i,η,γ ,ξ , представленная в виде следующего уравнения:

Пример. Найдем комплексные передаточные коэффициенты для процесса распространения тепла в цилиндрическом стержне, математическая модель которого имеет вид:

заданный коэффициент;

R, xL - заданные числа; x, r – пространственные координаты; τ − время. Граничные условия уравнения (1.18) имеют следующий вид:

17

*

(0 < R < R).

Условие (1.19) указывает на то, что концы стержня имеют постоянную температуру, равную нулю. Условие (1.21) является условием симметрии тепловых полей.

Входное воздействие распределено по границе, что отражает условие

(1.20).

Полагаем, что входное воздействие однозначно и может быть разложено в ряд Фурье по переменной x:

η = 1

где C1,η (τ)− коэффициент разложения в ряд Фурье функции U (x,τ); ψη −функция, определяемая из следующего соотношения:

(η =1,∞).

Для частотного анализа объекта положим в (1.22)

и найдем решение уравнения (1.18) при граничных условиях (1.19) – (1.21). Используя принцип суперпозиции, рассмотрим воздействие каждой составляющей ряда (1.22) на объект отдельно, а конечный результат найдем как алгебраическую сумму реакций от всех составляющих входного воздействия:

18

(η =1,∞),

где Hη (r, jω)−неизвестная функция.

Подставив (1.26) в (1.18) и преобразуя, получим уравнение для определения неизвестной функции Hη (r, jω):

Согласно / 20,21/, решение уравнения (1.27) имеет следующий вид:

Aη , Dη − коэффициенты, определяемые из граничных условий (20.18),

(20.19) (η =1,∞);

J0 , Y0 −функции Бесселя первого и второго рода нулевого порядка.

Так как температура на оси цилиндрического стержня из физических условий конечна, то в решениях должна отсутствовать функция Y0 , т.е.

Dη = 0 , (η =1,∞). Подставив (1.28) в (1.25) и в (1.20), определим значение коэффициента Aη , (η =1,∞):

19