Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov

3.2 Синтез регуляторов для распределенных систем управления с векторным входным воздействием

В предыдущих разделах были рассмотрены вопросы синтеза

инвариантных, а также при синтезе регуляторов, для систем управления с

устойчивости Найквиста разработана методика синтеза регуляторов для распределенных систем с векторным входным воздействием.

3.2.1 Общие замечания к синтезу систем, не принадлежащих к классу пространственно - инвариантных

Приведем основной результат, полученный в /35/ относительно обобщения критерия Найквиста на случай распределенных систем, структурная схема которых показана на рис. 5.1. (где К — скаляр; I — единичная матрица (m х m): G ( s ) - матрица размерами m x m, элементы которой являются рациональными функциями

G(s) = H (s) (D(s)) −1;

limdetD(s) =const≠0.

S→∞

Исследуя

в / 35 / показано, что если передаточная матрица разомкнутой системы не имеет полюсов, лежащих в правой полуплоскости S, то для устойчивости замкнутой системы достаточно, чтобы годографы вектора собственных значений (λi ( jω) ) не охватили точку с координатами

130

Re = −1/ K ; Im = 0 .

Рис. 3.9. Система управления.

Рис. 3.10. Распределенная система управления.

Рис. 3.11. Преобразованная структурная схема.

Полученный результат обобщается и на системы управления, структурная схема которых показана на рис. 3.10. (где R(x, s) -

передаточная функция регулятора). Полагаем, что регулятор принадлежит

пространственной координате; f (s) — вектор коэффициентов разложения

131

Так как регулятор обладает свойством пространственной инвариантности, то передаточная матрица регулятора имеет диагональную

воздействия на вектор, состоящий из тригонометрических функций. Если

Для асимптотической устойчивости системы, представленной на рис. 5.3, достаточно обеспечить асимптотическую устойчивость контура

1.

Передаточная матрица блока 1 (рис. 3.11) может быть записана на виде:

Ô(s) = [I +W R]−1 W R

Рассмотрим формирование структуры передаточной матрицы регулятора R . Положим, что регулятор выбран в виде идеального пространственно-интегрирующего звена, передаточная функция которого записывается в виде следующего соотношения:

Представляя входное воздействие в виде ряда Фурье по пространственным координатам, и определив передаточную функцию по каждой составляющей ряда входного воздействия, получим

132

(η =1, ∞) .

Передаточная матрица регулятора R может быть представлена в виде:

Таким образом, передаточная матрица разомкнутой системы имеет

вид

Если на вход системы, структурная схема которой приведена на рис. 3.11, подать входное воздействие

f (x, s) = C1(s) sin(Ψ1 x) ,

то на выходе разомкнутой системы будем иметь

Преобразуя (3.31), получим

133

∞

T (x, s) = С1(s) ∑Wi,1(s) R1,1(s) sin(Ψ1 x) . i=1

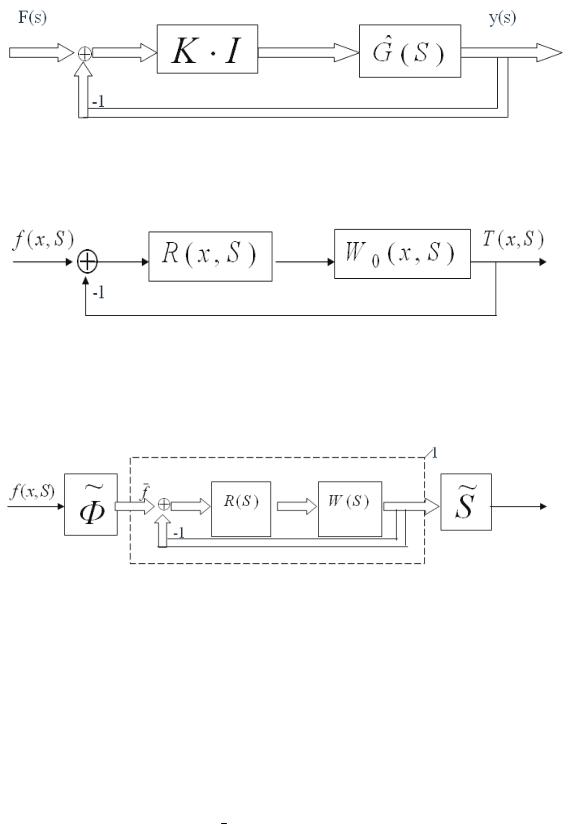
Рис. 3.12. Годографы собственных значений.

Подставляя в (3.30) S = jω , получим матрицу комплексных

передаточных коэффициентов разомкнутой системы.

Положим, что может быть определен бесконечный спектр

* *

собственных значений матрицы Фp ( j ω) (где ω — фиксированное

*

значение частоты ω [0, ∞]).

*

Изменяя значение ω от 0 до ∞ , построим годографы спектра собственных значений (при этом полагаем E4 и n4 — заданные числа). Пусть передаточная функция разомкнутой системы не имеет полюсов, лежащих в правой полуплоскости S, тогда для устойчивости замкнутой системы достаточно, чтобы бесконечный спектр годографов собственных

Re = −1, Im = 0 (на рис. 3.12 показаны годографы для первых четырех

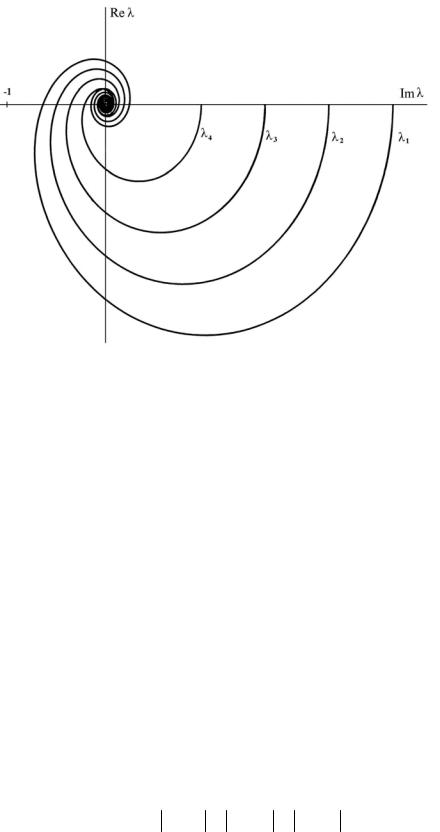
собственных значений). Для оценки устойчивости замкнутой системы могут быть использованы амплитудная и фазовая частотные характеристики годографов собственных значений. При построении характеристик будем полагать, что λ1(0) > λ2 (0) > λ3 (0) > ...

134

Рис. 3.13. Построение линий среза модуля и фазы. Аналогично п.2.4. строятся линии среза модуля и фазы разомкнутой

системы.

Интерпретация критерия Найквиста с учетом построенных частотных характеристик, приведенных на рис. 3.13, заключается в

135

следующем: пусть передаточная функция разомкнутой системы не имеет полюсов, лежащих в правой полуплоскости. Тогда для устойчивости замкнутой системы достаточно, чтобы линия среза модуля не имела с областью Г общих точек.

Используя полученную интерпретацию критерия Найквиста, можно определить значения коэффициентов E4, n4, при которых замкнутая система будет устойчива и запасы устойчивости годографов собственных значений по модулю и по фазе разомкнутой системы не менее заданных.

3.2.2 Синтез распределенных систем управления с векторным входным воздействием

Методику синтеза рассмотрим на примере синтеза регуляторов для системы управления температурным полем нагревательной камеры, используемой для термической обработки листовых заготовок 1 (см. рис. 3.14). Конструкция нагревательной камеры включает, корпус 2,

Постановка задачи: для системы управления температурным полем

нагревательной камеры синтезировать распределенные регуляторы R(1)(х, у, s) и R(2)(х, у, s), реализующие пропорционально-интегрально-

дифференциальные законы управления, с учетом ограничений на запасы устойчивости по фазе ϕ(ξ)

3.2.2.1 Анализ объекта управления

Для оценки динамических характеристик сформируем математическую модель объекта управления. При этом сделаем следующие допущения: температура на входе и выходе камеры поддерживается постоянной; тепловой поток через боковые стенки камеры

136

математическая модель объекта управления имеет вид:

Рис. 3.14. Нагревательная камера

Рис. 3.15. Структурная схема системы управления.

Граничные условия для системы уравнений (3.32) задаются

137

Полагая U2=0 и определяя комплексный передаточный коэффициент объекта по каждой составляющей ряда (3.34), получим

138

Aν(i,γ) и Bν(i,γ) определяется из следующего уравнения:

139