Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov

.pdf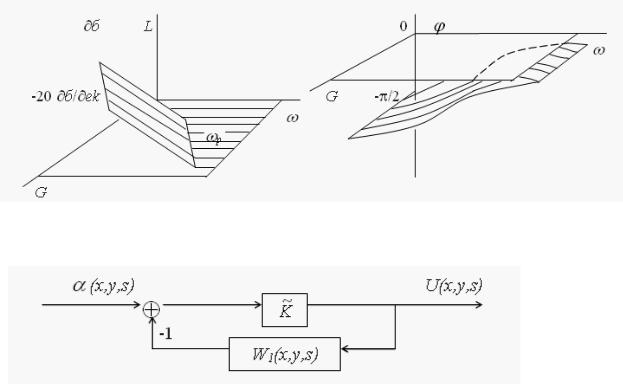

Скачиваний:

Добавлен:

21.03.2016

Размер:

3.83 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 217 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Рис. 2.7. Частотные поверхности

Рис. 2.8. Структурная схема устройства

6.Пространственно-усилительное звено, включенное

вобратную связь

Структурная схема пространственно-усилительного звена, включенного в обратную связь, приведена на рис. 2.8.

Подавая на вход рассматриваемого устройства воздействие (2.3), на выходе получим:

∞ 4

U (x, y, s) =

∑ ∑

n1 −1

(2.23)

η,γ =1ξ =1 1

+ K

(ψ

+ϕ

)

Cη,γ ,ξ (s) Bη,γ ,ξ (x, y),

где K - заданное число.

Статический коэффициент передачи, записанный с использованием обобщенной координаты, имеет вид:

(G) =

−1

1 + K

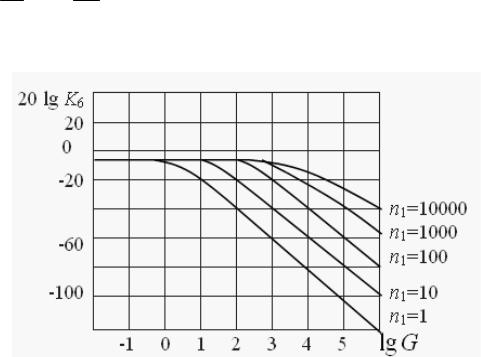
На рис. 2.9 приведены графики статического коэффициента усиления рассматриваемого устройства. При построении графиков полагалось E1=1;

=1.

Рассмотрим алгоритм моделирования рассматриваемого устройства

на ЦВМ.

Функция выхода рассматриваемого устройства связана с выходным

воздействием α следующим соотношением:

−1

U(x, y,s)=K

α(x, y,s)−E1

U(x, y,s)−

U(x, y,s) .

Дискретный аналог U(x,y,s) имеет вид:

α(xi, yν, s)−E1

n1 −1

U(xi, yν, s)

[U(xi−1, yν, s)−

U(xi, yν , s) = K

−

−2 U(x , y , s)+U(x , y , s)]

+[U(x , y , s)−2 U(x , y , s)+

i+1

ν−1

+U(x , y , s)]

(i =1, I; ν =1,

ϑ),

ν+1


где xi (i =			)- точки дискретизации по оси х, шаг дискретизации		х;
	1, I
yν (ν =				) - точки дискретизации по оси y, шаг дискретизации	y;
		1,ϑ

ϑ , I – заданные целые числа;

U (x0 , yν , s); U (xi+1, yν , s); U (xi , y0 , s); U (xi , yν +1, s) - граничные точки функции U(x,y,s).

Преобразуя полученную систему уравнений, придем к следующему результату:

α(xi , yν ,s)= A1 [U (xi−1, yν , s)+U (xi+1, yν ,s)]+ A2 [U (xi , yν −1,s)+

+U (xi , yν +1, s)]+ A3 U (xi , yν , s), (i =

; ν =

1, I

1,ϑ

где A

− E1

; A =

− E1

; A

E1 (n1 −1)

− 2 A

− 2 A .

n y2

Представим систему уравнений в матричном виде:

α = A U ,

где U T = [U1,1K,U1,ν ,K,U I ,1,KU I ,ϑ ];

αT = [α1,1K,α1,ν ,K,αI ,1,KαI ,ϑ ];

Ui,ν =U (xi , yν ,s);

αi,ν =α(xi , yν , s);

(i =1, I; ν =1,ϑ).

Рис. 2.9. Графики 20 lg K6 (G).

При этом полагалось, что значения функции U(x,y,s) в граничных точках равны нулю.

Значения функций выхода (см. рис. 2.8.)определяется из следующего уравнения:

U = A−1 α .

Если граничные условия функции U(x,y,s) не равны нулю, то необходимо соответствующим образом скорректировать матрицу А.

A3 A2 0K A1 0 K

A A

0 A 0K

2 3 2

0K0 A2 A3

00K A1

0 K

A 0 K

A A

3 2

A =

0 A1 0K A2 A3 A2 0

0 A1 0K

0K0 A

0K0 A A

0K0 A

2 3

0 K

0 A 0K

A A

0K0 A1

0K0 A2 A3

2.1.2 Техническая реализация распределенных звеньев

Техническую реализацию распределенных звеньев рассмотрим на примере реализации пространственно-изодромного звена, передаточная функция которого имеет вид (2.21). Если на вход звена подать воздействие α(x,y,s), то на выходе получим функцию (2.22).

Представим (2.22) в конечно-разностной форме. При этом обозначим шаг дискретизации по осям x и y через x и y соответственно. Число точек дискретизации по оси х равно N, а по оси y равно M. Тогда получим:

−1

(α

)

n,m

(s) = E

n,m

−

n−1,m

− 2α

n,m

+α

n+1,m

+ (αn,m−1 − 2αn.m +αn,m+1)

+αn,m ,

(2.24)

(n =1, N ; m =1, M ),

где αn,m =α(xn , ym , s).

Преобразуя (2.24), получим:

Un,m(s) =[K1 αn,m −K2 (αn−1,m −2αn,m +αn+1,m)−K3 (αn,m−1 −2αn,m +αn,m+1)]

1s +αn,m,

(n =1, N ; m =1, M ),

где K1 = E5

n5 −1

; K2 =

K3 =

;

Переходя от изображений Un,m (s) к оригиналам Un,m (τ ), получим:

Un,m(τ)=∫[K1

αn,m −K2

(αn−1,m −2αn,m

+αn+1,m)−K3

(αn,m−1 −

−2αn,m

+αn,m+1)]dτ +αn,m,

где αn,m (τ) - оригиналы функции αn,m (s);

α0,m (τ );αN +1,m (τ );αn,M +1(τ )

- значения функции αn,m (τ ) на границе.

Для вычисления управляющего воздействия ~n,m(τ) необходимо

знать состояние поля в n, m точках (n = 0, N +1; m = 0, M +1).

Положим, что состояние поля в этих точках известно, тогда алгоритм управления (2.24) может быть реализован на управляющей ЭВМ (цифровой вариант реализации) или с использованием операционных усилителей (аналоговый вариант /25/).

2.1.3 Распределенный высокоточный регулятор

Известно, что созданная в промышленности установка ВРТ (высокоточный регулятор температуры) позволила решить ряд задач управления температурой в заданной точке. Регулятор в этой установке состоит из усилительного дифференцирующего и интегрирующего звеньев. Из аналогичных распределенных звеньев сформируем структуру распределенного высокоточного регулятора (РВР).

Передаточная функция РВР имеет вид:

W (x, y, s)= E		n1 −1			−		1	2	+ E		n4 −1		−	1		2	1	+
W (x, y, s)= E					−	n		2	+ E				−	n		2	s	+
	1		n			n				4	n	4		n	4		s
			1				1					4			4			(2.25)
	n2 −1			1														(2.25)
+ E2	n2 −1			1			2	s.
			−
			−	n2
	n2			n2

Передаточная функция РВР, записанная с использованием обобщенной координаты, может быть представлена в виде следующего соотношения:

W (G, s)= E

n1 −1

+ E

n4 −1

+ E

n2 −1

s, 0 ≤ G ≤ ∞.

Для частотного анализа РВР положим в (2.26) S=jω модуль (М) и фазу (ϕ) функции W(G, jω):

M (G,ω)= K2 (G) ωω2 − K4 (G) 2 + (K1(G))2 12 ,

ϕ(G,ω)= arctg K2 (Gω) ωK2 (−GK) 4 (G) ,

n	i	−1		1			(i =1,2,4).
где Ki (G) = Ei			+		G	,
	ni			ni

(2.26)

и определим

(2.27)

(2.28)

Как следует из (2.28), минимальное значение модуля будет при

K2 (G) ω2 − K4 (G) = 0.	(2.29)
Преобразуем (2.29) к виду
lg K2 (G) + 2lgω = lg K4 (G )
или
lgω = 0,5 [lg K4 (G) − lg K2 (G)].	(2.30)

Минимальное значение модуля будет равно M min (G) = K1(G) .

На рис. 2.10 приведены частотные поверхности РВР. ГрафикиM min

совпадают с графиками коэффициента усиления пространственноусилительного звена, которые приведены на рис. 2.1.

Уравнение (2.30) определяет линию перегиба (ω(G)).

Рассмотрим решение уравнения (2.30). Пусть K2 (G) =1, тогда (2.30) преобразуется к виду lgω = 0,5 lg K4 (G) .

На рис. 2.11,а приведены графики lgω , построенные для случая

K2 =1.

Положим K4 (G) =1, тогда (2.30) преобразуется к виду

lgω = −0,5 lg K2 (G) .

Графики lgω приведены на рис. 2.11,б. Представим (2.30) в виде:

n4 −1

lgω = 0,5 lg E4 − 0,5 lg E2

−

+ 0,5 lg

(2.31)

n2 −1

− 0,5 lg

G .

Рис. 2.10. Частотные поверхности РВР.

Если n4 = n2 , то	(2.31) преобразуется к виду
lgω = 0,5	lg E4 − 0,5 lg E2 .	(2.32)
Графики функции lgω в этом случае будут в		виде прямых,

параллельных оси G.

Из (2.30) следует, что значение функции ω(G), удовлетворяющее уравнению, не изменяется, если K4 (G) и K2 (G) умножить на одно и тоже

~ (~ > )

постоянное число K K 0 . Определим, как изменяются при этом амплитудные характеристики.

~ =

Положим K 1, тогда из (2.27):

для ω → 0

получим M (G,ω)≈ K4

(G) ,

для ω → ∞ M (G,ω) ≈ K2 (G) ω .

Пусть K ≠1, тогда

K4 (G)ω ,

для ω → 0

получим M (G,ω)≈ K

для ω → ∞

K2 (G) ω .

M (G,ω) ≈ K

На рис. 2.12 приведен график изменения амплитудных характеристик

для фиксированного значения G = G1, при изменении K .

Обозначим

lg ω

= lg 1

, lgω

= lg(K

(G )),

(G )= lgω − lgω

K 2 (G1 )

(2.33)

Рис. 2.11. Графики линий перегиба.

Значение

(G1) связано с

следующим соотношением:

(G1 )+ 2 lg K1(G1)

(2.34)

≠1, то

Если K

lgω

= lg

(K2

(G1 )

~ , lgω = lg(K (G ) K ),

K )

(2.35)

(G1 )= lgω1

− lgω2 .

Вычитая (2.35) из (2.33) и преобразуя, получим

~	=	~

		(G1 )− (G1 )= −2 lg K .

Таким образом, изменяя значение K , можно влиять на характер изменения модуля (M(G,ω)) в окрестности линии перегиба (см. рис. 2.12).

Примечание. Методика синтеза распределенного высокоточного регулятора, рассмотренная ниже, предполагает, что значения точек перегиба амплитудной характеристики совпадают со значениями частот среза модуля разомкнутой системы. Вследствие параметрических возмущений определяются не точные значения частот среза модуля разомкнутой системы по каждой пространственной моде, а лишь некоторые области изменения частот среза модуля δν , (ν=1, 2, …). Для

учета области δν в методике синтеза используется параметр , который связан с параметром соотношением (2.34). Для выбора значения

может быть использовано соотношение δmax ≥ 3 , где δmax - максимальное значение последовательности δν , (ν=1, 2, …).

Рис. 2.12. Амплитудная характеристика.

2.2 Распределенные блоки 2.2.1 Объединение распределенных звеньев в блоки

В некоторых случаях приходится объединять распределенные звенья, образуя распределенные блоки.

Положим, что имеется распределенный блок, структурная схема которого приведена на рис. 2.13 (где W1 - передаточная функция

пространственно-усилительного звена W = 2 ;			E	0	- заданное число).
		1		0
На вход распределенного блока подано воздействие
~	N	4			(2.36)
α(x, y, s)=	∑ ∑Cη,γ ,ξ (s) Bη,γ ,ξ (x, y),				(2.36)

η,γ =1ξ =1

где N – заданное целое число.

Пусть требуется получить сигнал на выходе распределенного блока в виде

N	4
U (x, y, s)= ∑	Kη,γ ∑ Bη,γ ,ξ (x, y),	(2.37)
η,γ =1	ξ =1

где Kη,γ - заданные числа (η,γ =1, N ).

Рассмотрим утверждение, доказывающее возможность преобразования сигнала (2.36) в сигнал (2.37) блоком, структурная схема которого приведена на Рис. 2.13.

Утверждение. Для блока рассмотренной структуры существуют коэффициенты Ei (i =1,m), разрешающие задачу преобразования сигнала

(2.36) в сигнал (2.37).

Доказательство:

Подавая

на

вход распределенного блока

воздействие α(x, y, s) , на выходе будем иметь:

)

(−1)

U (x, y, s) = ∑Ei

∑

(ψη

+ϕγ

∑ Cη,γ ,ξ (s) Bη,γ ,ξ (x, y)

i=1

η,γ =1

ξ =1

+ E0

∑ ∑ Cη,γ ,ξ (s) Bη,γ ,ξ (x, y).

η,γ =1ξ =1

(2.38)

Рис. 2.13. Структурная схема распределенного блока.

Приравнивая (2.38) и (2.37), получим соотношение:

<<< < Предыдущая 1 2 3 4 5 67 / 217 8 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.03.201666.67 Кб9Biznes_plan.Docx
#
25.04.2019326.2 Кб2blablabla.docx
#
07.12.2018324.98 Кб36blablabla.docx
#
08.09.2019132.61 Кб1Blanki.doc
#
21.03.20161.19 Mб30book_holography_2009.pdf
#
21.03.20163.83 Mб14Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov.pdf
#
14.11.20191.28 Mб28BZhD_Laboratornaya_rabota_4.doc
#
21.04.2019536.06 Кб21C++ лекции.doc
#
21.03.2016358.65 Кб22C. Вводная лекция.pdf
#
21.03.2016534.94 Кб19C. Тема 1. Раздел 1.pdf
#
21.03.2016546.75 Кб18C. Тема 1. Раздел 10.pdf