
Bystrov_Grigorye_Pershin_-_Sintez_raspredelennykh_regulyatorov
.pdf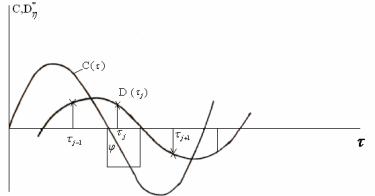
Рисунок 1.8. Графики C(τ),Dη (τ)
Управляющее воздействие (1.59) технически осуществляется следующим образом: на каждой секции секционного нагревателя во время эксперимента поддерживается тепловой поток:
|
|
|
|
π *η |
|
) ,(i = |
|
), |
||
α ( x |
,τ ) = q * sin( ω *τ ) * sin( |
* x |
1,m |
|||||||
|
||||||||||
i |
|
|
|
|
L |
i |
|
|
|
|
|
|
|
|
|
|
(1.60) |
|
|||
где xi |
(i = |
|
|
|
|
|
||||
1,m |
) - фиксированные числа (см. рис. 1.7). |
|||||||||
Таким образом, распределенное управляющее воздействие реализуется секционным нагревателем в виде ломаной линии (см. рис. 1.7).
При m →∞ломаная линия стремится к аппроксимируемой кривой. Положим, что число датчиков (n) таково, что возможно восстановить
температурное поле в камере на радиусе R (T(x,R ,τ)) . Восстанавливая температурное поле в τ j моменты времени
(j=l,2,...), разложим T(x,R ,τ |
j |
) в ряд Фурье: |
|||||||||||||||
|
|
|
|
~ |
|
|
|
|
|
|
|
~ |
|
|
|
|
|
T ( x, R ,τ |
|
|
|
(τ |
|
) * sin( |
π *η |
|
|
(τ |
|
) * cos( |
|||||
j |
) = ∑ D |
γ |
j |
L |
* x) + B |
γ |
j |
||||||||||
|
|
|
γ |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Если |
|
|
все |
коэффициенты |
||||||||||||
~ |
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(τ j ),(γ =1,∞) за |
|
|
|
|
|
|
||||||||||
Dγ |
(τ j ),Bγ |
|
исключением |
||||||||||||||
π L*γ * x).
~ |
разложения |
|
=η, равны нулю |
||
Dγ |
(близки к нулю, так как входное воздействие аппроксимировано ломаной линией), то объект принадлежит к классу пространственно-инвариантных.
Положим, что нагревательная камера обладает свойством пространственной инвариантности. Для вычисления частотных
характеристик строим график изменения C =q*sin(ω*τ) и график
30

|
|
~ |
|
изменения |
|
коэффициента Dγ=η(τj ) |
разложения функции |
T(x,R ,τ |
j |
) (см. рис. 1.8). |
|
|
|
|
|
По |
построенным графикам |
для фиксированной частоты |
|
(ω)определяем известными методами /37/ рассогласование фаз входного
и выходного сигналов (ϕ) и изменение модуля. |
|
|
||||
Проделав |
аналогичную |
процедуру |
при |
различных |
||
значениях |
ω, |
для |
каждого η |
контура |
можно |
построить |
частотные характеристики.
1.1.8 Пространственно-неинвариантные системы
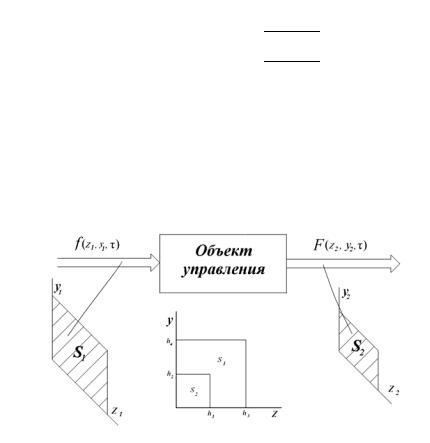
Некоторые результаты исследование этого класса систем приведены в / 11 /. Отметим, что достаточно широкий класс объектов с распределенными параметрами не принадлежит к классу пространственно-инвариантных. Рассмотрим пример, положим, что имеется объект представленный на рис.1.9, в котором протекают тепловые процессы
Рисунок1.9. Объект управления.
Математическая модель рассматриваемого объекта записывается в виде:
∂T |
|
2 |
T |
|
2 |
|
|
2 |
T |
|
|
|
||
|
∂ |
+ |
∂ T |
+ |
∂ |
|
, |
(1.61) |
||||||
∂τ |
= a |
∂x |
2 |
∂y |
2 |
∂z |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
0 ≤ x ≤ Lx ;0 ≤ y ≤ Ly (x, y, z);0 ≤ z ≤ Lz (x, y, z).
Где à -заданный параметр; Lx-заданное число; Ly (x, y, z), Lz (x, y, z) -заданные
функции, описывающие боковые поверхности, τ – время.
.
31
Граничные условия для рассматриваемого объекта описываются следующими соотношениями:
управляющее воздействие U(y, z, τ) распределено по границе S1
T(0, y, z, τ) = U(y, z, τ);
тепловой поток через границу S2 равен нулю
∂T ( L X |
, y , z , τ ) |
= 0 |
; |
|
∂x |
||||
|
|
|||
на остальных боковых поверхностях (S3, S4, S5, S6) поддерживается постоянная температура ( положим, что она равна 200 0С)
T(x, y , z, τ) = 200, x, y , z S3 S4 S5 S6 .
Начальные условия: T(x, y, z, τ=0) = 0.
Основные физические параметры моделируемого объекта приведены в таблице 1.1 ( параметры заданы в системе СИ).
Таблица. 1.1
Lx |
h3 |
h1 |
h4 |
h2 |
a |
0,5 |
0,2 |
0,05 |
0,2 |
0,05 |
0.4 · 10-5 |
Из рис. 1.9,1.10 видно, что пространственная область распределения входных воздействий (S1) и область распределения функции выхода (S2) при наложении не совпадают. В данном случае S1 > S2 следовательно объект не обладает свойством пространственной совместимости. Структурно данный объект представлен на рис.
Рисунок 1.10. Структурное представление объекта управления.
Совместим области S1 и S2 ( см. рис. 1.10 ). Используя рассмотренный выше метод для анализа таких систем (разлагая по собственным вектор-функциям оператора объекта) получим матрицу комплексных передаточных коэффициентов рассматриваемого объекта , связывающую пространственные моды входа и выхода объекта
32

управления. При разложении функций входа и выхода будем использовать параметры области S1.Полученная матрица комплексных передаточных коэффициентов будет полной ( недиагональной), т.е. объект не принадлежит к классу пространственно-инвариантных..
Рассмотрим построение дополнительного устройства (ДУ), которое проецирует область функции выхода (S2) на область входных воздействий (S1), при этом совокупность «ОУ+ДУ» обладает свойством пространственной совместимости. Отметим, что такой проектор может быть реализован как при помощи масштабного преобразователя (коэффициент усиления постоянен по пространственным координатам
(см. рис. 1.11)),
Рисунок 1.11. Области распределения входного воздействия S1 и функции
выхода S2 объекта управления.
так и в виде нелинейно функции, зависящей от пространственных координат, проектирующей область S1 на область S2 (см. рис. 1.12).
Рисунок 1.12. Области распределения входного воздействия S1 и функции
выхода S2 объекта управления.
Методику построения таких преобразователей рассмотрим на примере построения масштабного преобразователя для объекта, приведенного на рис.1.9. Представим входное воздействие на объект управления в виде:
|
|
|
|
|
_ |
|
, (1.62) |
|
f (ó1 , z1 ,τ)= 200 +100 sin(ψ j y1 ) sin |
ψk z1 |
|
||||
ψ j = |
π |
j , ψ k = |
|
|
|
|
|
π k (j = 1, ∞; k = 1, ∞). |
|
|
|
||||
|
|
_ |
___ |
___ |
|
|
|
|
h |
|
h |
|
|
|
|
|
3 |
|
4 |
|
|
|
|
33
Численное решение уравнения теплопроводности (1.61) с учетом граничных условий , показывает, что форма пространственных мод подаваемых на вход объекта (граница S1) сохраняется на выходе (граница S2), но при этом меняется только геометрия и амплитуда сигнала (см. рис. 1.13).
Рисунок 1.13. Пространственные моды: a - входного воздействия f (ó1 , z1 , τ)= T (0, ó1 , z1 , τ); б – функции выхода F0 = T (Lx , ó2 , z2 , τ).
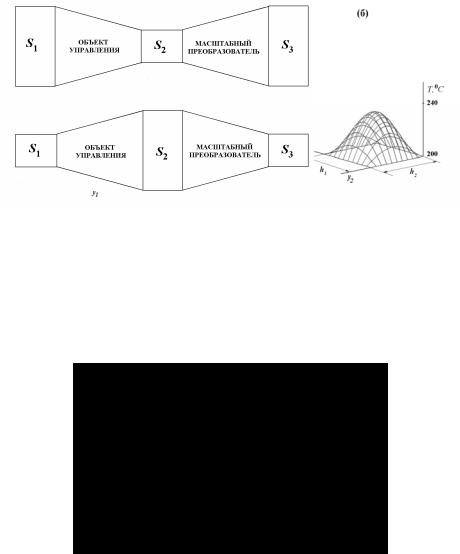
Масштабный преобразователь это устройство, которое изменяет геометрию пространственных мод на выходе объекта управления (см. рис. 1.14).
Рисунок 1.14. Блок-схемы преобразования.
Схема преобразования области распределения функции выхода объекта управления приведена на рис. 1.15.
34

Рисунок 1.15. Блок-схема «Объект + масштабный преобразователь».
Коэффициенты масштабного преобразования по координатам y и z могут быть определены по следующим формулам:
KY |
= |
h3 |
= |
0.2 |
= 4 , KZ |
= |
h4 |
= |
0.2 |
= 4 . |
|
|
0.05 |
h |
0.05 |
||||||||
|
|
h |
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
||
На рис.1.16 показано преобразование масштабным преобразователем координат области распределения функции выхода. Полученная область s3, при наложении, совпадает с областью s1.
Рис. 1.16. Преобразование координат.
На рис.1.17 показаны графики входного воздействия на объект управления и функции выхода масштабного преобразователя.
Рисунок 1.17. Пространственные моды: a- входного воздействия U (у,z,τ)=U (у1 ,z1 ,τ); б– функции выхода преобразователя
T (у3 ,z3 ,τ).
35

Применение масштабного преобразователя позволяет обеспечить пространственную совместимость системы состоящей из распределенных звеньев, что в свою очередь позволяет привести к классу ПИ распределенную систему. При этом матрица комплексных передаточных коэффициентов рассматриваемой системы (объект + масштабный преобразователь) имеет диагональный вид.
1.2 Характеристики устойчивости систем с распределенными параметрами.
1.2.1 Достаточное условие устойчивости распределенных систем
Положим, что замкнутую распределенную систему со скалярной функцией входа структурно можно представить бесконечной совокупностью независимых контуров.
|
|
|
|
|
|
η,γ ,ξ (η,γ = |
|
; ξ = |
|
) контуру |
|||
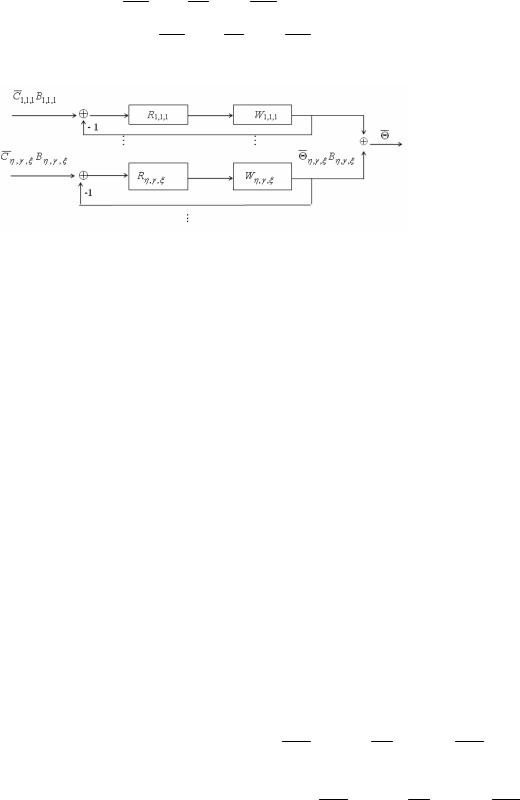
Пусть передаточная функция |
по |
1,∞ |
1,4 |
||||||||||
управления (см. рис. 2.1) имеет вид: |
|
|
|
|
|
|
|
|
|
||||
|
(s)= |
|
|
η,γ ,ξ (s) |
= |
Пη,γ ,ξ (s) |
|
|
|
|
|
||
Ф |
Θ |
|
|
|
|
|
|||||||
|
|
|
(s) |
|
|
|
|
|
|
|
|||
η,γ ,ξ |
|
|
Cη,γ ,ξ |
|
Мη,γ ,ξ (s) |
|
|
|
|
|
|||
|
|
|
|
, (1.63) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
∞
гдеПη,γ ,ξ (s)= ∑Пη,γ ,ξ,ν (s), ν =1
∞
Mη,ξ,γ (s)= ∑Mη,γ ,ξ ,μ (s) - целые аналитические
μ=1
функции,
Θη,γ,ξ (s) -преобразованная по Лапласу функция выхода.
Характеристическое уравнение по η,γ ,ξ (η,γ =1,∞; ξ =1,4) контуру
∞ |
|
|
∑Mη,γ ,ξ,μ (s)= 0 |
, (η,γ =1,∞; ξ =1,4). |
|
μ=1 |
(1.64) |
Решая уравнение (1.64), определим свободное движение в каждом контуре. Положим, что решение (1.64) найдено. Свободное движение в каждом контуре системы управления может быть определено из следующего соотношения:
Θη,γ ,ξ (τ )= ∑∞ Aη,γ ,ξ,μ exp(λη,γ ,ξ,μ τ) |
, (η,γ = |
|
; ξ = |
|
), |
μ=1 |
1,∞ |
1,4 |
|||
|
(1.65) |
|
|||
36
где λη,γ ,ξ,μ , (η,γ =1,∞; ξ =1,4; μ =1,∞)- корни уравнения (1.64);
Aη,γ ,ξ,μ , (η,γ =1,∞; ξ =1,4; μ =1,∞) - постоянные числа, определяемые начальными условиями .
Рисунок 1.18 Система управления В силу того, что контуры системы управления независимы, свободное
движение всей системы будет складываться из суммы свободных движений в каждом контуре системы управления, умноженных на
соответствующие |
пространственные |
моды: |
|
∞ |
4 |
∞ |
|
Θ(x, y,τ )= ∑ ∑ ∑Aη,γ ,ξ,μ exp(λη,γ ,ξ,μ τ) Bη,γ ,ξ(x, y) |
|
||
η,γ =1ξ =1μ=1
(1.66)
Будем считать, что система с распределенными параметрами, представленная на рис. 18, передаточная функция которой по каждому контуру управления имеет вид (1.63), является устойчивой, если
limΘ(x, y,τ )= 0 .
τ →∞
Утверждение 1. Для устойчивости системы с распределенными параметрами, свободное движение которой представляется в виде (1.66), достаточно, чтобы все корни λη,γ ,ξ,μ имели отрицательные
действительные части.
Доказательство:
Пусть
λη ,γ ,ξ , μ = ϑη ,γ ,ξ , μ + j ν~η ,γ ,ξ , μ ,
Aη,γ ,ξ,μ Λ (η,γ =1, ∞; ξ =1,4; μ =1, ∞),
где Λ - некоторая конечная область.
Полагая ϑη,γ ,ξ,μ < 0 для всех (η,γ =1, ∞; ξ =1,4; μ =1, ∞), ряд (1.66) промажорируем следующим рядом:
37
|
∞ 4 ∞ |
|
|
|
|
e |
(ϑ |
+ jν~ |
) τ |
Bη,γ ,ξ (x, y) |
≤ |
||
|
∑ ∑ ∑ Aη,γ ,ξ,μ |
|
|
η,γ ,ξ,μ |
η,γ ,ξ,μ |
|
|||||||
|
η,γ =1ξ=1μ=1 |
|
|
|
|
|
|
|
|
|
|
|
(1.67) |
|
∞ 4 ∞ |
− |
|
ϑ |
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
≤ ∑ ∑ ∑e |
|
|
min |
|
|
|
Amax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
η,γ =1ξ=1μ=1 |
|
|
|
|
|
|
|
|
|
|
|
|
так как функция e jν~η,γ ,ξ,μ τ B |
(x, y) ограничена. |
||||||||||||
|
|
|
|
|
|
|
|
η,γ ,ξ |
|
|
|
|
|
Amax - максимальный по модулю элемент, принадлежащий области Λ . - минимальный по модулю элемент, принадлежащий спектру
ϑη,γ ,ξ,μ при (η,γ = |
|
|
|
|
|
; |
|
|
ξ = |
|
|
|
|
|
|
|
|
|
|
|
|
μ = |
|
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
1, ∞ |
1,4; |
1, ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рассмотрим функцию |
|
|
|
|
|
∞ |
|
|
4 ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
ϑmin |
|
τ |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q = ∑ ∑ ∑ |
Amax |
e |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η,γ =1ξ=1μ=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Для нахождения |
|
lim Q рассмотрим усеченную функцию |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Q |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
N1 |
|
4 |
N2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
ϑmin |
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
Q = |
|
|
∑ ∑ ∑ |
Amax |
e |
|
|
, |
|
|
|
|
(1.68) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
η,γ =1ξ=1μ=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
где N1 , N2 , N3 |
- целые числа, которые могут быть выражены через N1 и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
коэффициенты K2 , K3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2 = K2 N1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N3 = K3 N1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(0 ≤ K2 < ∞; 0 ≤ K3 < ∞; 0 < N1 < ∞) . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Представим функцию (1.68) в виде |
|
|
|
|
|
− |
|
|
ϑmin |
|
K3 N1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Q = |
4 K2 N1 |
|
|
Amax |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Преобразуя, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
4 |
|
|
K2 |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
ϑmin |
|
K3 N1 |
|
|
|
|
|
max |
|
|
|
|
|
|||||||||||||||||||||||||||||
Найдем предел функции |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
lim |
|
|
= lim |
4 |
|
K2 |
|
N13 |
|
|
|
|
A |
|
|
|
|
(1.69) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
N1→∞ |
|
|
N1→∞ e |
|
ϑmin |
|
K3 N1 |
|
|
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Представим |
|
в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
Q1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϑmin |
|
K3 N1 . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
где |
|
|
= 4 K |
|
|
N |
3 |
|
|
A |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= e |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
Q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
38
Для исследования предела (1.69) определим производные функции Q1 и Q2 поN1 :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
dQ1 |
=12 K2 |
|
Amax |
|
N12 , |
|||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
Q1′ = |
|||||||||||||||||||||||||||||||
|
|
|
dN1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
′ |
|
|
|
dQ |
2 |
|
|
|
|
|
|
|
|
|
|
|
ϑ |
|
|
|
|
K |
N |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Q2 |
= |
|
|
|
|
|
|
= |
ϑmin |
K3 e |
|
|
|
min |
|
3 |
1 , |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
dN1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
″ |
= 24 K |
|
|
|
A |
|
N |
|
|
, |
|
|||||||||||||
|
|
|
|
|
|
Q |
2 |
|
|
1 |
|
||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
max |
|
|
|
|
|
|
||||||||||||
Q2″ = (ϑmin K3 )2 e ϑmin K3 N1 ,
Q1′′′= 24 K2 Amax ,
Q2′′′= (ϑmin K3 )3 e ϑmin K3 N1 ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Q1′ |
|
|
= ∞ , |
|
|
|
|
|
|
|
Q1″ |
|
∞ , |
|
|
|
|
|
|
|
|
|
||||||||||||
|
lim |
|
|
|
|
|
|
lim |
|
= |
|
lim |
Q1′′′ |
= 0. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
N |
→∞ |
|
|
|
|
′ |
|
|
|
∞ |
|
|
N →∞ |
|
|
|
″ |
∞ |
N |
1 |
→∞ Q ′′′ |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
1 |
|
Q2 |
|
|
|
|
|
|
|
|
1 |
|
Q2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||
Так как |
lim |
|
|
Q1′′′ = 0 , то по правилу Лопиталя |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
N1 →∞ Q2′′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
= |
|
lim |
|
|
|
Q1 |
|
= 0 . |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
N1 = ∞ |
|
|
|
|
N1 |
→∞ |
|
|
|
N1 →∞ Q2 |
Q(τ = ∞), |
|
|
|
|
|
|
|||||||||||||||||||||
При |
функция |
|
|
|
равна функции |
следовательно, |
|||||||||||||||||||||||||||||||||
Q |
|||||||||||||||||||||||||||||||||||||||
lim |
Q = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
N1→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Учитывая соотношение (1.68), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim θ (x, y,τ ) = 0 |
, |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
τ →∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
что и требовалось доказать.
Если на пространственно-инвариантную систему подано векторное входное воздействие, то свободное движение системы, может быть определено из следующего соотношения: где
m ∞ 4 ∞
θi ( x, y, τ) = ∑ ∑ ∑∑ Aχ,η, γ,ξ,μ eλ χ , η, γ , ξ , μ τ Bη, γ,ξ ( x, y) χ =1 η, γ =1 ξ=1 μ =1
где λχ,η,γ ,ξ,μ - корни характеристического уравнения по χ,η,γ ,ξ, μ контуру;
Аχ,η,γ ,ξ,μ , (η,γ =1, ∞; ξ =1,4; μ =1, ∞) – постоянные числа, определяемые начальными условиями;
39
