Добавил:

TooL Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

Теоретическая механика

Файл:

В. Д. Бертяев, Л. А. Булатов, В. В. Глаголев, В. И. Латышев, А. Г. Митяев. ЭВМ в курсе теоретической

.pdf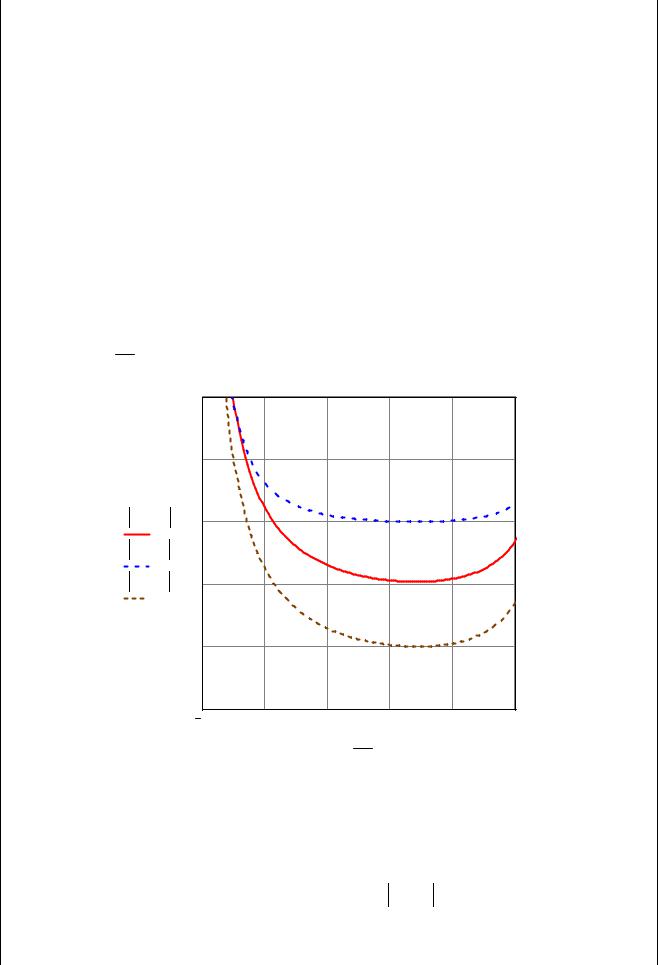

Скачиваний:

125

Добавлен:

22.01.2014

Размер:

3.24 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 247 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>

		Xa + Xc			Xa
		−Q + Ya + Yc			Xa
		−Q + Ya + Yc				Ya
	−2					Ya
	−2	b Q + b Yc − a Xc + M
	3	b Q + b Yc − a Xc + M				Xb
	3					Xb
		−P sin(α) + Xb − Xc		0	R(α) := Find Yb
		−P sin(α) + Xb − Xc
		−P cos (α) + Yb − Yc				Xc
					Yc

−P (c − s) + c cos (α) Yb + c sin(			α) Xb

Формируем векторы неизвестных реакций в виде двухэлементных матриц, их направление
относительно осиOx , а также вычисляем предельные значения параметра α.
RA(α) := submatrix(R(α),0,1,0,0)	αA(α) := atan2(RA(α)0,RA(α)1)
RB(α) := submatrix(R(α),2,3,0,0)	αB(α) := atan2(RB(α)0,RB(α)1)
RC(α) := submatrix(R(α),4,5,0,0)	αC(α) := atan2(RC(α)0,RC(α)1)

αmin := −π + γ							αmax:= π + γ
	2							2
α	deg− 1 = −33.69						α	deg− 1	= 146.31
	min							max
		π					Строим график зависимостей модулей реак-
α := αmin,αmin +		π	.. αmax				ций от параметра α, изменяющегося в ука-
		180					занном интервале.
							занном интервале.
				25
				20
			RA(α)	15
			RB(α)
			RC(α)	10
				5
				0	30	0	30	60	90	120
								α
								deg

Для вычисления параметра α, соответствующего минимальным значениям реакций связей используем элемент управления Radio Button (см. п. 4.10.2)

I :=	I :=	I :=
jlm\| Ra \|	ijlm\| Rb \|	jlm\| Rc \|

Объединим векторы реакций связей в матрицу, состоящую из трех столбцов, и сформируем

минимизируемую функцию.

R(α) := augment(RA(α),RB(α),RC(α)) Π(α) := R(α) I

Для нахождения минимальных значений реакций связей используем блок Given – Minimize, внутри которого укажем пределы изменения параметра α.

α := 0

Given

αmin ≤ α ≤ αmax

α' := Minimize(Π,α)

α'

= 72.412

Вычисление минимальных значений реакций связей

deg

4.766

RA(α')

(α') deg− 1

(α') =

= 10.194

= 62.123

9.011

14.299

RB(α')

(α') deg− 1

R (α') =

= 15

= 17.588

4.533

−4.766

(α )

(α') deg

− 1

= −162.412

R (α') =

−1.511

Осуществляем визуализации проведенных расчетов

Reference:C:\Program Files\Mathsoft\user_fun.mcd

Формируем векторы реакций связей для их отображения на графике.

Ra(α) := vector7(0,0,RA(α)0,RA(α)1,1)

Rb(α) := vector7

(0,0,RB(α)0,RB(α)1,1)

Rc(α) := vector7(0,0,RC(α)0,RC(α)1,1)

Ry(α) := augment(Ra(α) 1 ,Rb(α) 1 ,Rc(α) 1 )

Rx(α) := augment(Ra(α) 0 ,Rb(α) 0 ,Rc(α) 0 )

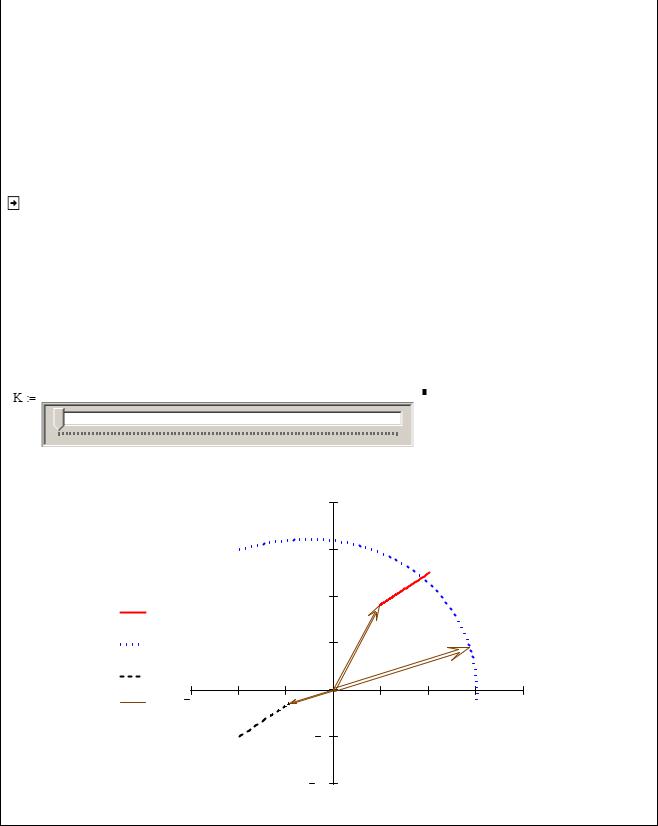
Используя элемент управления Slider , можно изобразить найденные величины при любом

значении угла α. Наличие символа " " рядом с переменными K и α′, свидетельствует об установленной, с помощью контекстного меню, опции Disable Evaluation (Отключить вы-

ражение)

α := 0,	π	.. π	α' :=	π	K		α'	= 72.412
						*
							deg
180		2	180

RA(α)1

RB(α)1

RC(α)1

Ry(α')

15		10		5	0	5	10	15	20

RA(α)0,RB(α)0,RC(α)0,Rx(α')

Таким образом, в задаче определены реакции связи и область существования решений уравнений равновесия. Решена задача оптимизации конструкции по одному параметру.

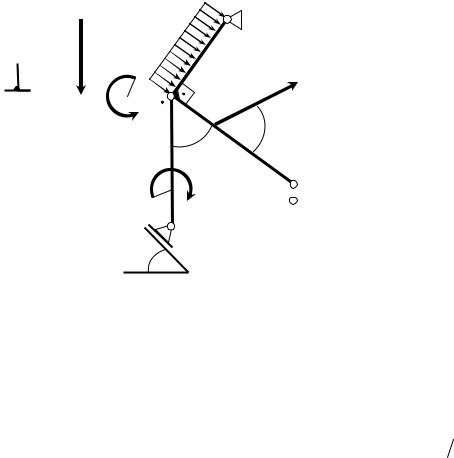
Пример 2. Равновесие трех тел

Конструкция состоит из жесткого угольника CED и двух стержней AE и BE , которые шарнирно соединены друг с другом в точке E (рис. 2.2.4). Внешними связями, наложенными на конструкцию, являются неподвижная опора, приложенная в точке D , катковая опора в точке B , невесомый стержень в точке C и скользящая заделка в точке A . Конструкция находится в равновесии под

действием пар сил с моментами M1

и M2 , сосредоточенных сил

P2 , а так-

же распределенной нагрузки постоянной интенсивности q .

α1

Рис. 2.2.4 Конструкция из трех звеньев

Найтиреакциивнешнихивнутреннихсвязейвточках A , B , C ,

D и E если

AE = 3 м,

BE = 2 м,

CE = 4 м,

DE =1 м,

AL = 2 м,

CK = 3 м,

α = π6 ,

β = π4 ,

γ = π3 ,

M1 =10 кН м,

M2 =10 кН м, P1 = 20 кН,

P2 = 20 кН,

q = 5 кН м.

Определить условия, при которых конструкция находится в равновесии. Указать области значений внутренних параметров конструкции, внутри которых модули реакции связей не превышают значение Fпр =100 кН .

Решение

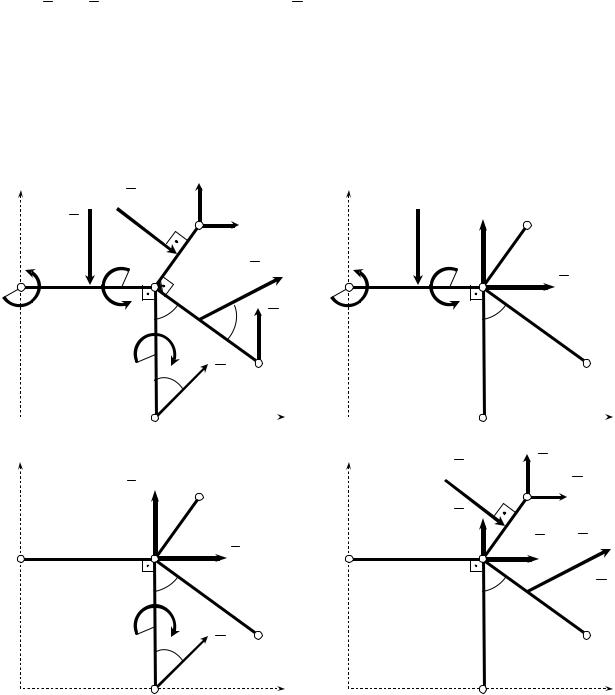
Проведем координатные оси xOy (рис. 2.2.5 а) и изобразим на схеме,

действующие на конструкцию внешние силы: пары сил с моментами M1 и M2 ,

силы P1 и P2 , равнодействующую Q от действия распределенной нагрузки

(Q = q a) постоянной интенсивности q , приложенную в точке N , а также реак-

ции внешних связей. Для нахождения реакций внешних и внутренних связей расчленим конструкцию и рассмотрим равновесие каждой ее части отдельно

(рис. 2.2.5 б, в, г):

y	Q
	P2
MA	E	N
A	E
	L

M1 γ

	Y	D			y
			X
				D		Y
				D	P2	Y	E 1
D					P2		E 1	D
D								D

	P1	A	MA	E
					XE 1
K α			L
		RC			γ
			M1

	M2	RB	C			C

O a )		β	x	O б)		x
		B			B

YE 2

A	E	XE 2	A

Q YD

YE 3		D
	N	XE 3	P1
E

γ K αRC

M2		RB	C			C

O в)		β	x	O г )		x
		B			B
	Рис. 2.2.5 Расчетные схемы узлов конструкции.
Стержень	AE (рис. 2.2.5 б). Изобразим действующие на стержень силы:
пару сил с моментом M1 , силу				и реакции связей. Реакцию скользящей за-
			P2

делки A изображаем парой сил с моментом M A , а реакции шарнира E изобра-

жаем двумя составляющими: X E1 , YE1 .

Стержень BE (рис. 2.2.5 в). Изобразим действующие на стержень силы:

пару сил с моментом M2 и реакции связей. Реакцию RB катковой опоры B на-

правим перпендикулярно опорной плоскости, а реакции шарнира E изобража-

ем двумя составляющими: X E 2 , YE 2 .

Угольник DEC (рис. 2.2.5 г). Изобразим действующие на угольник силы:

равнодействующую

, приложенную в

точке

распределенной нагрузки Q

N EN = 1 DE , силу

и реакции связей. Реакции неподвижной опоры

D и

D ,

шарнира E изобразим двумя составляющими: X

YD и X E 3 , YE 3 , а усилие RC в

стержне C направим вдоль его оси.

Все звенья механической системы: стержень

AE , стержень BE и уголь-

ник DEC находятся в равновесии под действием произвольной плоской системы сил и для каждого из них можно записать по три независимых уравнений равновесия, например

AE, BE, CED : ∑Fkx = 0,	∑Fky = 0,	∑M E (Fk )= 0.
k	k	k

Таким образом, общее число независимых уравнений равновесия равно девяти. Число неизвестных величин, в девяти уравнениях — одиннадцать (реакции

M A , RB , RC , X D , YD , X E 1 , YE1 , X E 2 , YE 2 , X E 3 , YE 3 ).

Учтем, что шарнирE , в котором соединены звенья конструкции, ненагружен, т.е., согласно аксиоме о равенстве действия и противодействия, должно выполняться равенство

RE 1 + RE 2 + RE 3 = 0,

которое в проекциях на оси координат примет вид

Е: ∑Fkx = 0; X E 1 + X E 2 + X E 3 = 0,

∑Fky = 0; YE 1 +YE 2 +YE 3 = 0. k

Окончательно имеем одиннадцать уравнений и столько же неизвестных реакций. Задача является статически определимой.

Формируем активные силы, действующие на конструкцию

P1 sin(α + γ)

Q sin(γ)

P1 :=

−

cos

(α + γ)

P2 :=

−P

F :=

−

(γ)

M1 :=

M2 :=

Q cos

−M

Формируем выражения для реакций связей

Rb sin(β)

:= Rb cos (β)

R :=

Xe1

Xe2

Xe3

Ye1

Ye2

Ye3

Определяем радиус-векторы точек приложения действующих внешних сил.

:= BE

ED cos (γ)

(γ)

ED cos

EK sin

EC sin

:= r +

ED sin(γ)

:= r

ED sin(γ)

:= r

−EK cos (γ)

:= r +

−EC cos (γ)

Q E

D E

K E

C E

Вычисление главного вектора

и главного момента M E внешних сил, действующих на

стержень AE .

Xe1

PAE := P2 + RE1

+ Ye1

→ −P

MeAE := MA + (rL − rE)× P2 + M1 + (rE − rE)× RE1 MeAE → Ma −

Вычисление главного вектора PBE и главного момента M E стерженьBC .

0
0
0
(AL − AE) P	+ M
2	1

внешних сил, действующих на

Rb sin(β) + Xe2

PBE:= RB + RE2 PBE → Rb cos (β) + Ye2

										0
Me		:= (r − r )× R + M2 + (r − r )× R								0
Me	BE	:= (r − r )× R + M2 + (r − r )× R				Me	BE	→		0
	BE	B E	B	E E	E2		BE
									BE Rb sin(β) − M
											2

Вычисление главного вектора PCD и главного момента M E внешних сил, действующих на угольникCED .

P sin(α + γ) + Xe3 + Q sin(γ) + Xd

PCD := RC + P1 + RE3 + FQ + RD

→ Rc − P cos (α + γ)

+ Ye3 − Q cos (γ) + Yd

:= (r − r )

× R + (r − r

)

× P1 + (r − r

)× R + (r − r

)× F +

(r − r )× R

C E

C K E

E E

E3 Q E

Q D

expand

MeCD

simplify→

(γ)

sin

(α)

−

(γ)

−

(γ)

EC sin

EK P

ED Q

ED cos

ED sin

Вычисление главного вектора внутренних сил, действующих в шарниреE .

								Xe1 + Xe2 + Xe3
PE := RE1 + RE2 + RE3							PE →
PE := RE1 + RE2 + RE3							PE →	Ye1 + Ye2 + Ye3
								0
Формирование ортов		,		,		декартовой системы координат.
Формирование ортов	i	,	j	,	k	декартовой системы координат.
1						0		0
i := 0						j := 1		k :=	0

0						0			1

Формируем и вычисляем левую часть уравнений равновесия

EQ := (PAE i PBE i PCD i PE i PAE j PBE j PCD j PE j MeAE k MeBE k MeCD k)T

Xe1

Rb sin(β) + Xe2

P1 sin(α) cos (γ) + P1 cos (α) sin(γ) + Xe3 + Q sin(γ) + Xd

Xe1 + Xe2 + Xe3

−P2 + Ye1

expand

Rb cos (β) + Ye2

simplify→

Rc − P

cos (α) cos (γ) + P sin(α) sin(γ)

+ Ye3 − Q cos (γ) + Yd

Ye1 + Ye2 + Ye3

Ma − P2 AL + P2 AE + M1

BE Rb sin(β) − M2

(γ)

(α) − 1

(γ)

−

(

γ)

EC sin

EK P

sin

ED Q

ED cos

ED sin

Вводим исходные данные для расчета

AE := 2	BE:= 1	AL := 1	ED := 3	EC:= 4	EK := 1	α :=	π	β :=	π	γ :=	π
							6		4		3
M1 := 15	M2 := 20	P1 := 10	P2 := 30	q := 5

Задаем начальное приближение для неизвестных реакций.

Ma		0
	Rb		0

	Rc		0
	Xd		0
	Yd		0
	Yd		0
Xe1		:= 0
	Ye1		0
	Xe2		0
	Xe2		0
	Ye2		0
	Xe3		0

	Ye3		0

Given

Вычисляем равнодействующую Q распределенной нагрузки, постоянной интенсивностиq .

Q := q ED *

Q = 15

Задаем начало блока решений системы уравнений "Given", и формируем систему уравнений равновесия с помощью операций копирования и вставки.

Xe1

Rb sin(β) + Xe2

P1 sin(α) cos (γ) + P1 cos (α) sin(γ) + Xe3 + Q sin(γ) + Xd

Xe1 + Xe2 + Xe3

−P2 + Ye1

Rb cos (β) + Ye2

− P

cos (α) cos (γ) + P sin(α) sin(γ)

+ Ye3 − Q cos (γ) + Yd

Ye1 + Ye2 + Ye3

Ma − P2 AL + P2 AE + M1

BE Rb sin(β) − M2

(γ)

(α) − 1

(γ)

−

(

γ)

EC sin

EK P

sin

ED Q

ED cos

ED sin

Ma		Ma
	Rb		Rb

	Rc		Rc
	Xd		Xd
	Yd		Yd
	Yd		Yd
Xe1		:= Find Xe1
	Ye1		Ye1
	Xe2		Xe2
	Xe2		Xe2
Ye2		Ye2
	Xe3		Xe3

	Ye3		Ye3

Ma
				0
	Rb
			0	-45

	Rc		1	28.284

	Xd		2	-61.322
	Yd		3	-42.99

			4	78.822
Xe1		=
			5	0
	Ye1
			6	30
	Xe2

			7	-20
	Ye2
			8	-20
	Xe3
			9	20

Ye3			10	-10

Вычисляем неизвестные реакции связей с помощью процедурыFind , которая указывает окончание блока решения системы уравнений.

Формируем векторы реакций внешних и внутренних связей, действующих на конструкцию. Вычисляем модули реакций и их ориентацию относительно декартовой системы координат.

− 1

MA :=

αA := acos

deg

Rb sin(β)

R :=

(β)

:= acos

deg− 1

Rb cos

− 1

RC :=

αC := acos

deg

− 1

RD :=

αD := acos

deg

Xe1

− 1

RE1 :=

Ye1

αE1

:= acos

deg

Xe2

− 1

RE2 :=

Ye2

αE2

:= acos

deg

Xe3

− 1

RE3 :=

Ye3

αE3

:= acos

deg

		0					90
MA =		0	MA	= 45	αA =		90



	−45					180

RB =

= 28.284

αB =

= 61.322

RC =

−61.322

αC =

180

−42.99

118.609

= 89.783

28.609

RD =

78.822

αD =

RE1 =

RE1

= 30

αE1 =

−20

135

−20

RE2

= 28.284

135

26.565

= 22.361

= 116.565

−10

RE3

Расчет	многозвенных конструкций с помощью блока решений
Given − Find	не требует знания программирования и матричной алгебры, но в

тоже время не позволяет получить исчерпывающую информацию при исследовании найденных решений уравнений равновесия. Применение же матричных методов, особенно при решении систем линейных алгебраических уравнений, позволяет провести исследование найденных решений в полном объеме.

С другой стороны, использование матричных методов в явной форме: то есть, прямое задание матрицы коэффициентов при неизвестных величинах и вектора правой части уравнений равновесия ограничено в Mathcad системой десяти уравнении. В том случае, если число неизвестных больше десяти, необходимо применять или методы программирования, или блочную форму записи искомых матриц, с последующим применением функций объединения stack иaugment , или другие методы, вытекающие из условий задачи.

В данной задаче систему одиннадцати линейных алгебраических уравнений можно уменьшить до девяти, применив аксиому о равенстве действия и противодействия, расчленив, например, конструкцию на две части, AEB и CED . В этом случае уравнения связей примут вид

RE 3 = −RE′ 3 = −RE 1 − RE 2 .

После этого можно использовать матричный метод решения в явном виде. Пример формирования уравнений равновесия, а затем матрицы коэффициентов и вектора правой части, представлен ниже.

……………….

Формируем выражения для реакций связей

……………….

	Xe1			Xe2			:= −1 (R		)
R	:=	Ye1	R	:=	Ye2	R	:= −1 (R	+ R	)
E1			E2			E3	E1	E2
		0			0

………………..

Формируем и вычисляем левую часть уравнений равновесия

EQ := (PAE i

PAE j MeAE k PBE i

PBE j MeBE k

PCD i PCD j

MeCD k)T

Xe1

−P2 + Ye1

Ma − P2 AL + P2 AE + M1

Rb sin(β) + Xe2

expand

(β) +

Ye2

Rb cos

→

(β) −

simplify

BE Rb sin

P sin(α) cos (γ)

+ P cos (α) sin(γ) − Xe1 − Xe2 + Q sin(γ)

+ Xd

Rc − P1 cos (α) cos

(γ) + P1 sin(α) sin(γ) − Ye1 − Ye2 − Q cos (γ) + Yd

EC sin(γ) Rc + EK P sin(α) −

ED Q + ED cos (γ)

Yd − ED sin(γ) Xd

Формируем матрицы коэффициентов A и вектор правых частей уравнений равновесияB .

0		0	0	0	0	1	0	0	0
	0	0	0	0	0	0	1	0	0
	0	0	0	0	0	0	1	0	0
	1	0	0	0	0	0	0	0	0
	0	sin(β)	0	0	0	0	0	1	0
		cos (β)
A(β,γ) := 0		cos (β)	0	0	0	0	0	0	1	*
		BE sin(β)								*
	0	BE sin(β)	0	0	0	0	0	0	0
	0	0	0	1	0	−1	0	−1	0
	0	0	0	1	0	−1	0	−1	0
	0	0	1	0	1	0	−1	0	−1
	0	0	1	0	1	0	−1	0	−1
0		0	EC sin(γ)	−ED sin(γ)	ED cos (γ)	0	0	0	0

<<< < Предыдущая 1 2 3 4 5 67 / 247 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 > Следующая >>>