
В. Д. Бертяев, Л. А. Булатов, В. В. Глаголев, В. И. Латышев, А. Г. Митяев. ЭВМ в курсе теоретической
.pdf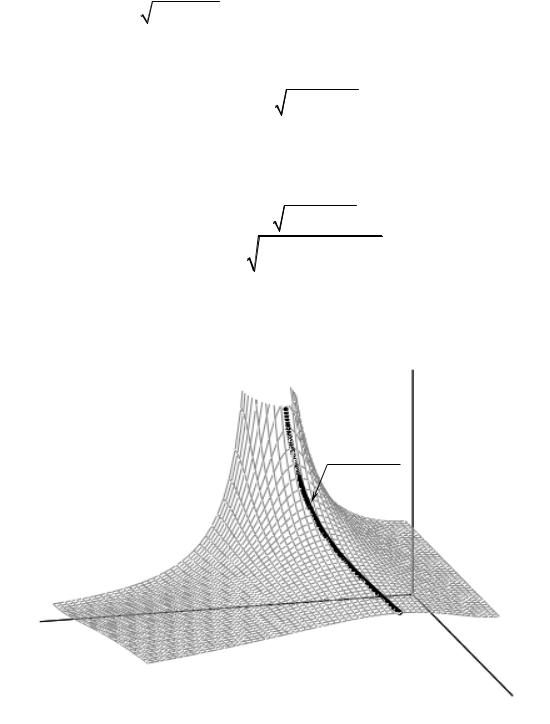
Q = −λ F |
sin(pt +ϕ − β |
0 |
)+ |
2n p cos(pt +ϕ − β |
0 |
) |
||||
0 |
|
|
|
k |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Здесь λ — коэффициент динамичности. |
|
|
|
|
|
|
||||
Данное выражение может быть преобразовано к виду |
|
|
||||||||
Q = −λ F |
1+ 4ν 2 z2 |
sin(pt +ϕ − β |
0 |
), где tg (δ ) = 2ν z |
||||||
0 |
|
|
|
|
|
|
|
|
|
|
Максимальное значение Q равно |
|
|
|
|
|
|
|
|
|
|
|
Q = λ F 1+ 4ν 2 |
z2 |
|
|
||||||
|
max |
0 |
|
|
|
|
|
|
|
|
Отношение наибольшей силы, передаваемой основанию, к амплитуде возмущающей силы называется коэффициентом передачи силы K (см. рис. 2.3.5):
K (z, ν )= |
|
1+ 4ν 2 |
z2 |
|
|
|
||||
( |
|
2 |
) |
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
||||||
|
1− z |
|
+ |
4ν |
z |
|||||
|
|
|
|
|
|
|||||
Коэффициент передачи силы для амортизатора совпадает с коэффициен-
том динамически только при отсутствии демпфирования (n = 0).
K
max (K )
z
ν
Рис. 2.3.5 Коэффициентпередачисилы K (z, ν)
101
Максимальные значения коэффициента передачи силы достигаются при следующих значениях z
z = 21ν 
Коэффициент передачи сил характеризует качество виброзащиты. При жёстком соединении (c = 0, β = 0) амортизируемого объекта и основания —
K =1. При K <1 виброзащита эффективна. Амплитуда силы Qmax , действую-
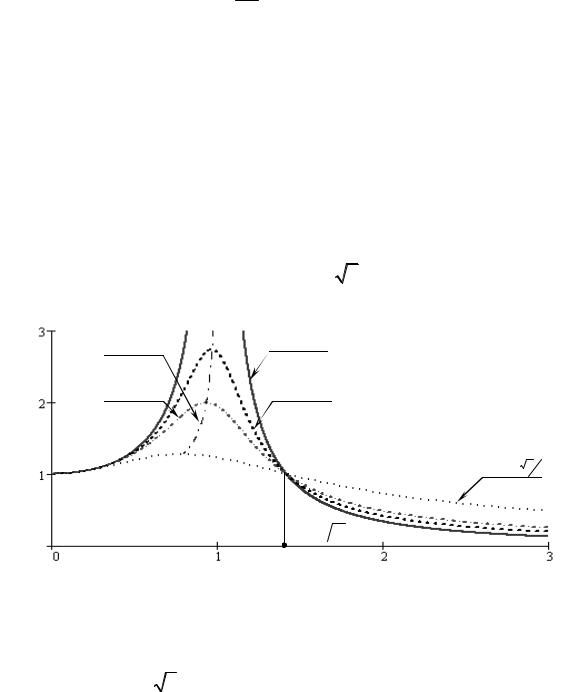
щей на основание, уменьшается. При K >1 применение амортизатора нецелесообразно. На рис. 2.3.6 изображён графики сечений поверхности K (z, ν)
(рис. 2.3.5) при различных значенияхν . Все кривые, независимо от демпфиро-
вания, пересекаются в точке с координатами ( 2; 1) (рис. 2.3.6).
K |
max (K ) |
ν = 0 |
|
|
|
|
ν = 0.3 |
ν = 0.2 |
ν = 2 2
z =  2
2
z
Рис. 2.3.6 Сечения поверхности K (z, ν ) при фиксированных значениях ν
Следовательно, чтобы Qmax была меньше амплитуды F0 , должно быть выполнено условие z > 2 . Обычно принимают z > 4 .
Условия, обеспечивающие соответствие движений механических систем их математической модели
Исследование колебательных систем с помощью коэффициентов динамичности λ(z, ν) и (или) коэффициента передачи силы K (z, ν) позволяют оп-
102
ределить точки или области на поверхностях λ(z, ν) , K (z, ν) , указывающие относительные величины максимальных амплитуд обобщенной координаты и обобщенной силы.
В тоже время, даже при малых значениях коэффициентов λ(z, ν) ,
K (z, ν) , возможны такие состояния, когда амплитуды некоторых внутренних обобщенных сил будут таковы, что их величины будут находиться вне области допустимых значений (предел прочности, движение без проскальзывания т.д.), обеспечивающих нормальное функционирование механической системы.
В силу вышесказанного возникает задача разработки таких критериев, которые позволят определять области допустимых значений внутренних параметров механической системе при ее движениях согласно принятой математической модели. В качестве внутренних параметров механической системы примем величины обобщенных масс каждого тела системы и обобщенную жесткость упругого элемента.
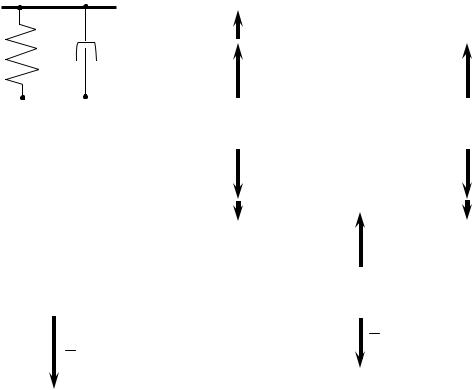
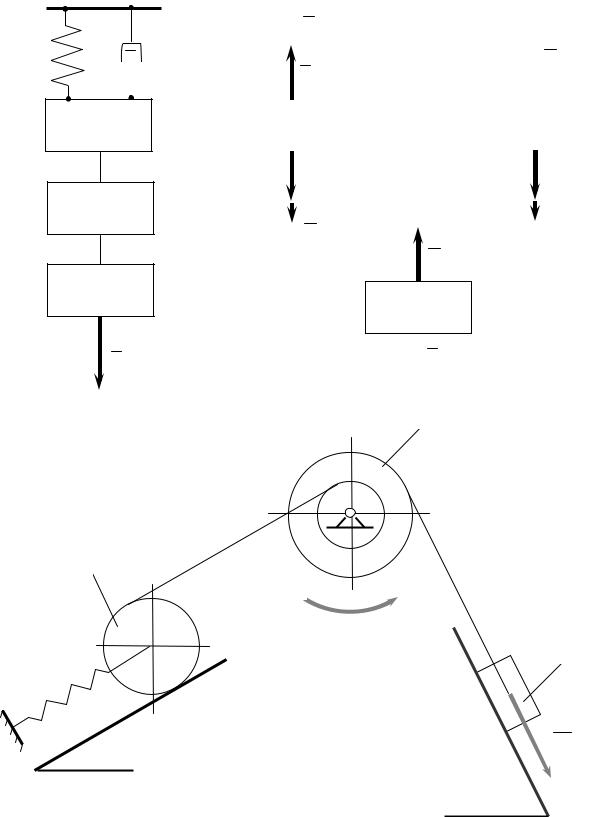
Рассмотрим механическую систему с одной степенью свободы, состоящую из N тел (рис. 2.3.7). Предположим, что на каждое тело системы действуют голономные, стационарные и идеальные связи (гибкие нити, опорные плоскости, стержни и т.д.). Расчленим механическую систему на составные части и применим к каждому телу системы одну из теорем динамики: теорему об изменении количества движения, теорему об изменении кинетического момента. С учетом кинематических связей, наложенных на систему, уравнения движения тел системы, не нарушая общности, можно представить в следующем виде
m1 q = F − R1,
.... … ,
mj q = Fj + Rj − RN′ −1,
.... … ,
mN q = FN + RN −1 −c q − β q.
103
где Fj — обобщенные активные силы, Rj — обобщенные силы реакции внут-
ренних связей, mj обобщенные (приведенные) массы тел механической систе-
мы, c — обобщенная жесткость, β — обобщенный коэффициент сопротивле-
ния, q, q, q — обобщенные координата, скорость и ускорение соответственно.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FR |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′N −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
||||||
|
|
|
|
|
|
|
Fупр |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
mN |
|
|
|
mN |
|
|
|
|
|
|
mj |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
j |
||||
|
|
|
|
|
|
|
R N−1 |
|
|
|
|||||||||||
|
m j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fj |
|||||
|
|
|
|
|
|
F |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F
F
Рис. 2.3.7 Расчетная схема.
Разрешая данные уравнения относительно неизвестных величин получим соотношения для реакций, выраженные через обобщенные координаты, скорости и ускорения, а также дифференциальное уравнение, описывающее движение механической системы
R1 = F1 − m1 q;
... … …;
Rj = Fj − mj q;
... … …;
RN −1 = FN − mN q; m q + β q + c q = F,
решение которого, при заданных начальных условиях, соответствует выражению
104

q = A0 e−nt sin(k′t +α0 )+ B0 sin(pt +ϕ − β0 )
После дифференцирования обобщенное ускорение можно представить в виде:
|
|
q = −B p2 |
sin (pt +ϕ − β |
0 |
)+ |
χ e−n t sin (k′t +α |
0 |
+ 2ψ ) |
|
|
|
|||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
tg (ψ )= |
n |
= |
ν |
— фазовый угол, |
χ = |
A k2 |
— безразмерный множи- |
||||||||||||||
|
|
0 |
|
|||||||||||||||||||
k′ |
1−ν 2 |
B0 |
p2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
тель, для которого выполняется условие |
|
χ ≤ χ* , |
χ* = |
k |
|
|
1 |
|
= 2 |
n |
λ |
— |
||||||||||
|
p |
|
|
1−ν 2 |
|
p |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
||||
значение множителя при нулевых начальных условиях.
Выражения для неизвестных реакций окончательно можно записать следующим образом
Rj = Fj + mj B0 p2 sin (pt +ϕ − β0 )+ χ e−n t sin (k′t +α0 + 2ψ )
Для обеспечения движения тел механической системы необходимо выполнение дополнительных условий, наложенных на эти соотношения. Применительно к указанным связям эти условия должны обеспечивать:
o Отсутствие деформаций стержней,
o Положительность сил натяжения канатов и тросов
o Отсутствие проскальзывания при движении тел относительно друг друга. Поскольку величины указанных реакций являются функциями не только
времени но и внутренних параметров механической системы (масс тел и жесткости упругого элемента), то данные условия в общем виде можно переписать в следующей форме
|
|
|
|
|
|
Tj (m1, |
m2 , ...,mN ,c, t )≥ 0, |
|
|
|
|
|
|
Rj (m1, |
m2 , ...,mN ,c, t )≥ 0 |
где Tj |
— силы натяжения канатов, если они существуют, Rj — реакции внеш- |
||||||
них |
и |
внутренних связей, R*j — |
предельное значение данных реакций, а |
||||
Rj |
= R*j − |
|
Rj |
|
. |
|
|
|
|
|
|||||
105
Для нахождения границ областей выполнения этих условий, необходимо найти корни следующих уравнений
Tj (m1, m2 , ...,mN ,c, t ) = 0,
Rj (m1, m2 , ...,mN ,c, t )= 0
Для исключения параметра t проинтегрируем данные уравнения по времени, воспользовавшись следующим свойством аналитических функций
|
t |
|
||
|
∫ |
|||
I (a) = |
|
f (a,t) |
− |
f (a,t) dt ≥ 0 , |
|
0 |
|
|
|
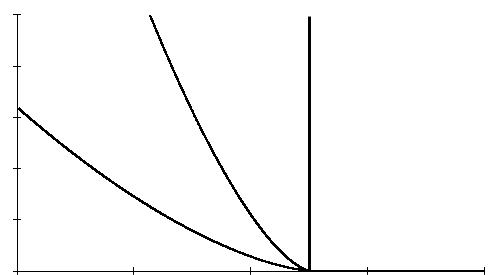
в котором равенство нулю интеграла I(a) |
осуществляется при выполнении ус- |
|||
ловия f (a,t) ≥ 0 t ≥ 0 (см. рис. 2.3.8).
Вычисляя предел данного выражения при t → ∞ получим, что значения
несобственного интеграла I (a) равны |
|
|
|
||||||||||||||
I (a) = lim t |
|
|
|
|
f (a,t) |
|
|
|
− f (a,t) dt = |
0 a ≥ amin |
, |
||||||
|
|
||||||||||||||||
t→∞ ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
a < a |
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
min |
|
что характерно для сил натяжения Tj , или |
|
|
|
||||||||||||||
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
a ≤ amax |
|
I (a) = limt→∞ ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
f (a,t) |
|
− |
f (a,t) dt = |
|
|
|||||||||||
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
a > amax |
|
что характерно для функций Rj = R*j |
− |
|
Rj |
|
. |
|
|
|
|||||||||
|
|
|
|
|
|||||||||||||
При численном вычислении несобственные интегралы с бесконечным пределом интегрирования заменяем собственными интегралами с конечным пределом интегрирования, и будем решать следующую систему уравнений
|
|
|
|
m |
= min I |
|
|
(m ) = 0 , |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
k min |
mk |
|
Tj |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
m |
= max I |
|
(m ) |
= 0 |
, |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
k max |
mk |
|
|
Rj |
k |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
τK |
|
|
|
|
|
|
|
|
|
|
|
τK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
IRj (mk ) = ∫ |
|
|
Rj |
|
− |
|
|
, |
|
(m1 ) = ∫ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||||||||||||
|
|
|
Rj dt |
m2 |
ITj |
|
|
Tj |
|
−Tj dt |
|
m2 . |
|||||||||
|
0 |
|
|
|
|
|
|
m3 |
|
|
|
|
|
0 |
|
|
|
|
|
|
m3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
c |
106
I(a) |
τ1 ≤ τ2 |
τk = τ2 |
τk = ∞ |
τk = τ1
I(a) = 0
a a
Рис. 2.3.8 Характерное поведение функции I(a) при разных значениях τk
В качестве верхнего предела интегрирования можно выбрать время установления τУ [5], которое задается с указанной точностью ε . Величину τУ вы-
числяем по формуле:
τy = −1n ln (ε χ)
Необходимо отметить следующее. При движениях системы вблизи критических состояний, таких как биения и резонанс, происходит резкое изменение формы колебательного процесса, и в этом случае интегралы не будут являться монотонно убывающими функциями, а могут иметь локальные минимумы, максимумы и наличие нескольких корней уравнений.
Следовательно, величину τУ , с удовлетворительной степенью точности можно использовать при вычислении интегралов в диапазоне параметров, далеких от критических состояний.
Вблизи резонансных состояний требуется проведение дополнительных исследований.
107
Приближенное решение
Для приближенной оценки границ области допустимых значений внутренних параметров механической системы часто рассматривается состояние установившегося движения. В этом случае закон движения системы определяется выражением:
q = B0 sin(pt +ϕ − β0 ).
Выражения обобщенных реакций, действующих на каждое тело механической системы, имеют вид
Rj = Fj (mk , ck , t )+ mj B0 (mk , ck , t ) p2 sin(pt +ϕ − β0 ).
Приняв sin(pt +ϕ − β0 ) = ±1, дополнительные условия можно переписать сле-
дующимобразом
Tmin j = Fj (mk , ck )− mj B0 (mk , ck ) p2 ≥ 0, Rj = Fj (mk , ck )+ mj B0 (mk , ck )p2 ≥ 0.
Таким образом, область допустимых значений внутренних параметров механической системы будет определена на границе, которая задается уравнениями
Fj (mk , ck )− mj B0 (mk , ck ) p2 = 0,
Fj (mk , ck )+ mj B0 (mk , ck )p2 = 0.
108

2.3.2. ИССЛЕДОВАНИЕМЕХАНИЧЕСКОЙСИСТЕМЫ СОДНОЙСТЕПЕНЬЮ СВОБОДЫ
Рассмотрим поведение трехмассовой системы (рис. 2.3.9), в которой тела, с массами равными — m1 , m2 , m3 соответственно, соединены идеальными гиб-
кими связями (канатами), а одно из тел движется плоско – параллельно без скольжения. Коэффициент сцепления — fСЦ . Движение происходит под дейст-
вием возмущающей силы, модуль которой изменяется по закону
F (t )= F0 sin(pt ), в среде с сопротивлением, пропорциональным первой степе-
ни скорости. Коэффициент вязкого трения — μ . На одно из тел системы дейст-
вует упругая связь, жесткость которой c . Массами канатов и упругого элемента пренебрегаем.
Для определенности примем следующие исходные данные:
Тело 1: |
m1 |
= 1 кг |
|
|
|
Тело 2: |
m2 |
= 2 кг |
r2 = 0.15 м |
R2 = 0.3 м |
i2 = 0.2 м |
Тело 3: |
m3 |
= 3 кг |
r3 = 0.2 м |
сплошной цилиндр |
|
|
μ = 0.2 Н м с |
c = 2000 Н/м |
fСЦ = 0.3 |
|
|
|
α = 60° |
β = 30° |
|
|
|
|
F0 = 10 Н |
p = π/2 рад/с |
|
|
|
Начальные условия: |
при t = 0 |
s0 = 0.03 м |
s0 = v0 = 0.04м/c |
||
В качестве примера рассмотрим следующую задачу.
Требуется исследовать движение механической системы и определить область допустимых значений ее параметров (масс тел и жесткости упругого элемента), обеспечивающих ее работоспособность.1
1 Изменение демпфирующих свойств в данной задаче не рассматриваются.
109
m3
m 2
m1
F
3
 β
β
 FR
FR
 T23
T23
Fупр
m3 |
|
|
|
m2 |
|||||
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
T |
|||
|
T32 |
|
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
F2 |
||
|
|
F |
|
|
|
||||
|
|
сц |
|
|
|
|
|
||
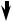 F3
F3
T12
m1
 F
F
2
Мc
1
F (t)
α 
Рис. 2.3.9 Динамическая модель и ее конкретизация
110
