10.3.6. Входное сопротивление длинной линии

На рис. 10.5 показано схему использования длинной линии на практике. Рассмотрим линию с волновым сопротивлением Z_В длиной l. Пусть линия возбуждается генератором гармонических сигналов с выходным комплексным сопротивлением Z_Г. На конце линия нагружена комплексным сопротивлением Z_Н.

Рис. 10.5. Схема использования длинной линии на практике

В произвольном сечении длинной линии, нагруженной комплексным сопротивлением , электрическое состояние может быть записано как

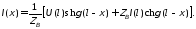
По отношению к генератору длинная линия в сечении x=0 является нагрузкой. Как нагрузка, линия характеризуется входным сопротивлением Z_ВХ. Найдем комплексные амплитуды напряжения и тока в начале линии

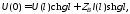
а зная их, определим и входное сопротивление

(10.30)

Из полученной формулы (10.30) видим, что входное сопротивление нагруженной длинной линии является функцией четырех переменных – . Рассмотрим несколько характерных случаев, возникающих на практике.

1. Входное сопротивление нагрузки равно волновому сопротивлению длинной линии 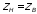. В этом случае, как видно из формулы (10.30) 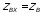, нагрузка согласована, нет отраженной волны, в линии существует только прямая волна, распространяющаяся от генератора к нагрузке. Такой режим работы длинной линии называетсярежимом бегущей волны.

2. Линия обладает большим затуханием . В этом случае 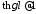и, как видно из формулы (10.30), также. При этом амплитуда отраженной волны пренебрежимо мала, и в линии устанавливается, практически, режим бегущей волны. Отрезки цепей с распределенными параметрами с большим затуханием на практике используют в качестве согласованных нагрузок (например, в СВЧ диапазоне).

3. В линии без потерь или с очень малыми потерями коэффициент распространения 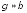,, и поэтому, сделав в (10.30) замену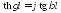, получим

(10.31)

1. При коротком замыкании линии сопротивление нагрузки , формула (10.31) принимает вид

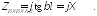(10.32)

График зависимости от нормированной длины линии врежиме короткого замыкания приведен на рис. 10.6.

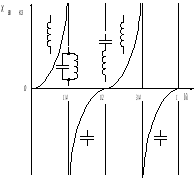
Рис. 10.6. Зависимость 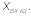линии в режиме короткого замыкания от ее нормированной длины

3.2. При разомкнутой линии на конце сопротивление нагрузки 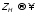(режим холостого хода), и формула (10.31) принимает вид

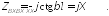(10.33)

График зависимости 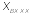от нормированной длины линии в режиме холостого хода приведен на рис. 10.7.

При фиксированной длине линии в формулах (10.32) и (10.33) можно рассматривать как функцию частоты.

10.4. Комплексный коэффициент передачи и передаточная функция системы с длинной линией

10.4.1. Постановка задачи

Рассмотрим систему, в которой посредством длинной линии осуществляется передача сигналов от источника к потребителю (рис. 10.8а). Исчерпывающей характеристикой, ориентированной на анализ такого процесса в линейных системах спектральным методом, является комплексная передаточная функция системы .

Методом комплексных амплитуд исследуем систему в режиме гармонических колебаний, найдем комплексный коэффициент передачи и, рассматривая частотув качестве независимой переменной, получим функцию.

Рис. 10.7. Зависимость 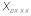линии в режиме холостого хода от ее нормированной длины

Представим генератор гармонических колебаний в виде последовательно соединенных источника напряжения и комплексного сопротивления(рис. 10.8а). Параметрами линии передачи служат постоянная распространения и волновое сопротивление.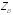

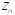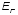Нагрузку линии передачи представим комплексным сопротивлением . Значения сопротивлений,,в общем случае различны. В качестве входного колебания будем рассматривать напряжение источника, а в качестве выходного – напряжение на сопротивлении нагрузки, т.е. на конце линии. Охарактеризуем эти сигналы комплексными амплитудамии.

Определим комплексный коэффициент передачи напряжения отношением

.

(10.34)

Имеется два способа получить формулу, определяющую этот коэффициент. Ниже покажем оба приема.