10.3.2. Прямые и обратные волны

Выясним физический смысл слагаемых, входящих в общее решение

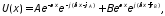
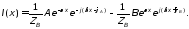
_{Перейдем от распределения комплексных амплитуд} и к распределению мгновенных значений напряжения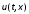и тока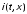

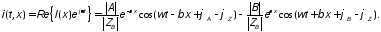
Волновой процесс – перенос в пространстве состояния постоянной фазы. В первых слагаемых 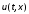и ,положив фазу постоянной, определим фазовую скорость

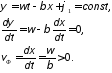(10.15)

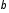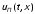Так как величины иположительные, то положительный знак фазовой скорости указывает на то, что первые слагаемые описывают волны, распространяющиеся в сторону увеличения координаты(от генератора). Такие волны называютпрямыми волнами. Распределения их мгновенных значений будем обозначать и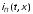, а распределения комплексных амплитуд –и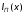.Из (10.15) следует связь постоянной распространения с фазовой скоростью и длиной волны

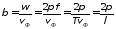(10.15а)

Для вторых слагаемых, поступив таким же образом, получим

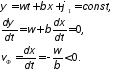(10.16)

Видим, что в этом случае фазовая скорость имеет отрицательный знак. Это указывает на то, что вторые слагаемые описывают волны, распространяющиеся в сторону уменьшения координаты (к генератору). Такие волны называютсяобратными волнами. Распределения мгновенных значений обратных волн будем обозначать и, а распределения комплексных амплитуд –и.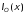

Таким образом, общее решение телеграфных уравнений имеет смысл наложения волн, бегущих навстречу друг другу. Пользуясь понятиями прямых и обратных волн, общее решение волнового уравнения можно записать как

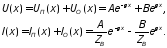(10.17)

Из (10.17) виден физический смысл волнового сопротивления: – коэффициент пропорциональности между комплексными амплитудами прямых (обратных) волн напряжения и тока.

10.3.3. Отражение волн в длинной линии

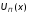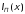Рассмотрим систему с однородной длинной линией, представленную на (рис. 10.2). Генератор, подключенный к началу линии слева, при 0, возбуждает в ней прямые волныи. Справа на ее конце, при, линия нагружена сопротивлением, представляющим неоднородность. Прямые волны, падающие на неоднородность частично отражаются. 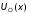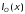Любая неоднородность на пути распространения прямых волни, которые в такой постановке задачи называютпадающими, вызывает их отражение – появление обратных волн и, которые называютотраженными. Характеристикой явления отражения служат коэффициенты отражения по напряжению 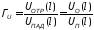и по току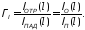

Граничное условие при определяется выражением 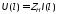. Из общего решения имеем

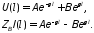(10.18)

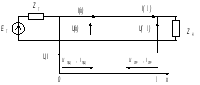
Рис. 10.2 Отражение волн в линии, нагруженной на конце сопротивлением

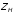
Отсюда находим комплексные амплитуды прямой (падающей) и обратной (отраженной) волны .

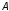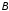Определив комплексные амплитуды и, запишем распределение напряжение и тока в произвольном сечении длинной линии

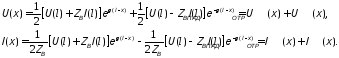(10.19)

С учетом этих выражений коэффициенты отражения по напряжению и по току в сечении 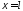определятся формулами

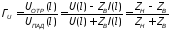, (10.20)

. (10.21)

10.3.4. Интерференция прямых и обратных волн

При наличии прямой (падающей) и обратной (отраженной) волны наблюдается физическое явление интерференции. Рассмотрим результат наложения прямой и обратной волн напряжения, бегущих в противоположных направлениях

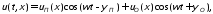(10.22)

где

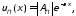
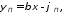
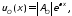
На основании принципа суперпозиции двух волн одинаковой частоты выражение (10.22) можно записать в виде

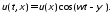(10.23)

Здесь

(10.24)

описывают распределение результирующей амплитуды вдоль линии (интерференционную картину) и их начальных фаз, а

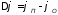(10.25)

– разность начальных фаз прямой и обратной волн.

Сомножитель третьего слагаемого в (10.24) 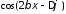определяет положение максимумов и минимумовинтерференционной картины. Вдоль линии в местах, где выполняется условие

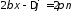, n=0, 1, 2,… (10.26)

наблюдаются максимумы, равные 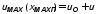, а в местах, гдевыполняется условие

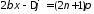, n=0, 1, 2,… (10.27)

наблюдаются минимумы, равные . Положения максимумов и минимумов вдоль линии определяются, как следует из (10.26) и (10.27), выражениями

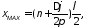
. (10.28)

Следует отметить, что в максимумах мощность результирующей волны больше суммы мощностей прямой и обратной волн, а в минимумах мощность результирующей волны меньше разности их мощностей. Это указывает на то, что интерференция волн приводит к распределению мощности вдоль линии. Распределение результирующей амплитуды вдоль линии является периодической функцией. 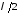В результате этого соседние максимумы (минимумы) наблюдаются на расстояниях , а минимумы наблюдаются на расстоянияхот ближайших максимумов.

В линии без потерь и с очень малыми потерями все максимумы и минимумы одинаковы по амплитуде. На практике для оценки степени согласования нагрузки с линией вводится параметр коэффициент стоячей волны по напряжению (КСВН)

(10.29)

Используя формулы (10.20), (10.21) и (10.29), определим характерные значения коэффициентов отражения и режимы длинной линии при разных значениях сопротивления нагрузки Z_Н.

Если сопротивление нагрузки равно волновому сопротивлению длинной линии Z_Н=Z_В, то такая нагрузка называется согласованной, при этом 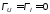. В длинной линии существует только падающая волна. Такой идеальный режим переноса энергии от генератора в нагрузку называется режимом бегущей волны.

Если Z_Н=0 (короткое замыкание на конце линии), тогда 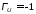,а . В этом случае на конце линии амплитуды отраженных волн напряжения и тока равны амплитудам падающих волн напряжения и тока. При этом отраженная и падающая волны напряжения находятся в противофазе, а отраженная и падающая волны тока – синфазные.

Если Z_Н=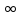 (линия разомкнута на конце, холостой ход), тогда , а. В этом случае на конце линии амплитуды отраженных волн напряжения и тока тоже равны амплитудам падающих волн напряжения и тока. Однако отраженная и падающая волны напряжения – синфазные, а отраженная и падающая волны тока находятся в противофазе.

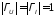
В случаях, когда амплитуды отраженных и падающих волн равны, то есть , в линии наблюдается режим стоячих волн.

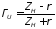Когда сопротивление нагрузки является активным Z_Н=R_H и не равным ,то и 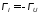. В этом случае на конце линии амплитуды отраженных волн меньше амплитуд падающих волн и в линии наблюдается режим смешанных волн. Распределения амплитуд напряжения и токов в окрестности конца линии при разных значениях сопротивления нагрузки Z_Н показаны на рис. 10.3.

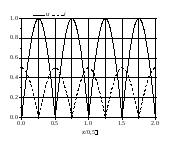
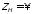
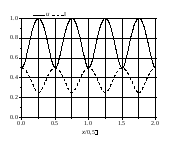
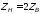
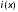Рис. 10.3. Распределения и в окрестности конца линии