7.3.2. Угловая модуляция

В зависимости от того, каким параметром высокочастотного колебания управляет низкочастотное колебание, различаютчастотную и фазовую модуляцию.

При частотной модуляции частота является функцией :

, (7.14)

где – частота несущего колебания,– коэффициент.

Поскольку частота – это скорость изменения фазового угла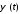, то частотно модулированный сигнал в общем виде можно представить как

. (7.15)

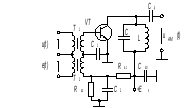
а)

б)

Рис. 6.4. Амплитудный модулятор

а) схема модулятора, в котором осуществляется базовая амплитудная модуляция;

б) графическое объяснение процесса модуляции

При фазовой модуляции функцией является фаза. При этом сигнал с фазовой модуляцией в общем случае примет виде:

. (7.16)

Рассматривая мгновенное значение частоты как скорость изменения фазового угла , получим:

. (7.17)

Из приведенных выражений (7.14) – (7.17) видим, что как при частотной, так и при фазовой модуляции происходит изменение и частоты, и фазы, а в результате и фазового угла . Поэтому эти два вида модуляции рассматривают какугловую модуляцию.

В случае частотной модуляции одним тоном управляющего низкочастотного сигнала мгновенное значение частоты имеет вид

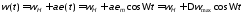, (7.18)

где – максимальное отклонение значения частоты от несущей частоты, которое называютдевиацией частоты.

После выполнения в (7.15) интегрирования высокочастотный сигнал, частотно модулированный одним тоном, запишем как

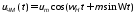. (7.19)

Здесь параметр характеризует максимальное отклонение фазы и называетсяиндексом модуляции.

Отметим, что при фазовой модуляции одним тоном индекс модуляции , а девиация частоты.

Рассмотрим амплитудный спектр высокочастотного ЧМ сигнала, модулированного одним тоном. Для этого преобразуем (7.19)

(7.20)

Из теории специальных функций известно, что иможно представить в виде

(7.21)

Подставив (7.21) в (7.20) можно видеть, что спектр модулированного одним тоном ЧМ сигнала содержит бесконечный набор гармоник. Однако вкладом в амплитудный спектр гармоник с номерами можно пренебречь, поскольку значения функций Бесселястановятся очень малыми (см. рис. 7.5, на котором показаны функции Бесселя порядка=0, 1, 2)..

В виду этого, ширину спектра ЧМ сигнала при больших индексах модуляции () принимают равной

, (7.22)

т.е. ширина спектра равна удвоенной девиации частоты

Следует также отметить, что при индексах модуляции () становится подавленной амплитуда несущего колебания. Это способствует тому, что основная часть мощности передатчика ЧМ сигнала сосредоточена в боковых полосах спектра, несущих информацию.

Частотную модуляцию наиболее просто можно осуществить, управляя частотой высокочастотного колебания автогенератора, путем перестройки колебательного контура с помощью варикапа. Вариант схемы частотного модулятора с варикапом на основе 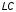– автогенератора (емкостная трехточка), представлен на рис. 7.6а. Варикап, подключенный параллельно колебательному контуру, управляет его резонансной частотойи, следовательно, частотой высокочастотных колебаний автогенератора.

Известно, что барьерная емкость варикапа (обратно смещенного -перехода) существенно зависит от приложенного напряжения и определяется вольт-фарадной характеристикой(рис. 7.6б).

_{В режиме покоя (модулирующий сигнал отключен) емкость варикапа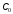} определяется напряжением смещения . Если точку покоя выбрать в линейной области вольт-фарадной характеристики варикапа, то емкость варикапабудет изменяться во времени относительнопо закону, действующего на входе автогенератора модулирующего сигнала. Например, если, тои тогда при

. (7.23)

Рис. 7.5 Функции Бесселя порядка =0, 1, 2

а) б)

Рис. 7.6. Частотный модулятор

а) схема частотного модулятора с варикапом;

б) вольт-фарадная характеристика варикапа и временные диаграммы, поясняющие изменение его емкости