Лекция №5 Понятие функции комплексного переменного.

Рассмотрим в комплексной плоскости (Z) два множества E и D (не пустые).

Отображение множества на множествоназываетсяфункцией комплексного переменного (D может принадлежать другой плоскости (W)). Любому Z₀, принадлежащему E, указан каким-то способом одним элемент из D).

Пусть Z = x+i·y, W = u+i·v. Очевидно, что задание функции комплексного переменного эквивалентно следующему: каждой паре (Е здесь принадлежит декартовой плоскости) ставится в соответствие два числа v и u. Следовательно, задание функции комплексного переменного W = f(Z) эквивалентно заданию вещественных функций u = u(x,y), v = v(x,y). При этом мы имеем f(Z) = u(x,y) + i·v(x,y).

Функция u(x,y) называется вещественной частью функции f(Z), а v(x,y) мнимой частью f(Z). Таким образом, Ref(Z) = u(x,y) , Imf(Z) = v(x,y).

Например, для функции W = Z² = (x +i·y)² = x² – y² + 2·i·x·y вещественная часть ReZ² = x² – y², ImZ² = 2·x·y.

Геометрически, как отображение множества на множество.

В теории аналитических функций рассматривают и многозначные функции.

Функция W = f(Z), отображающая множество на множествоназываетсямногозначной, если она ставит в соответствие некоторым не одно, а несколько числовых значений.

Пример.

1. Функция W = Zⁿ (n = 1, 2, …) является однозначной функцией комплексного переменного.

2. Функция является n-значной функцией. Только для 0 и ∞ одно значение.

3. W = Arg Z является бесконечно-значной функцией. Она определяется во всей плоскости (Z) \ ({0} и бесконечность) = arg Z + 2·k·π (k = 0, ±1, ±2, …).

Предел функции комплексного переменного

Пусть функция f(Z) задана на множестве иZ₀, принадлежащей (Z), предельная точка множества Е.

Комплексное число A = B+i·C называется пределом функции W = f(Z) в точке Z₀, если для любого , такое что, для любой точкиZ принадлежащей E (Z ≠ Z₀), удовлетворяющее неравенству (1), выполняется неравенство(2). При этом пишут

(3).

В дальнейшем мы будем просто писать (4).

Теорема.

Для того чтобы число A = B+i·C было пределом функции W = f(Z) при Z→Z₀, необходимо и достаточно, чтобы выполнялись равенства

(5), (6).

Доказательство.

Мы воспользуемся следующими очевидными неравенствами:

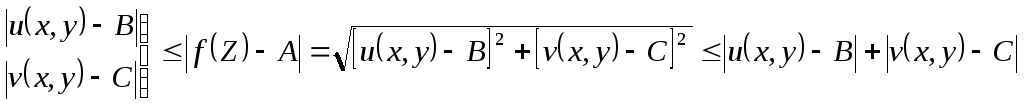(7)

Необходимость. Пусть выполняется равенство (3). Покажем, что справедливы равенства (5) и (6). Возьмем любое ε > 0, очевидно, что для него существует такое число δ > 0, что для любой точки Z принадлежащей E (Z≠Z₀), удовлетворяющее неравенству , выполняется неравенство.

Возьмем число , тогда для любой точки(x,y) принадлежащей E, отличной от (x₀,y₀), такой что ,, будет выполняться неравенствои, следовательно, будет|f(Z)–A|<ε. Поэтому в силу левой части неравенств (7) будет |u(x,y)–B|<ε, |v(x,y)–C|< ε. Значит, выполняются равенства (5) и (6).

Достаточность. Пусть теперь выполняются равенства (5) и (6). Покажем, что (4). Возьмем любое, в силу (5) и (6) найдется, такой что, для любой точки(x,y), принадлежащей E, отличной от (x₀,y₀), удовлетворяющей неравенствам (8) ,, будут выполняться неравенства,(9).

Легко видеть, что для любой точки Z принадлежащей E (Z ≠ Z₀), удовлетворяющей неравенству , подавно будут выполняться неравенства,. Поэтому будут выполняться неравенства (9), но тогда в силу правой части неравенств (7) для этих точекZ будет выполняться неравенство . Следовательно,.

Итак, существование предела комплексной функции эквивалентно существованию предела двух вещественных функций от двух переменных. Поэтому, на пределы функции комплексного переменного распространяются все основные функции пределов функции вещественной переменной. В частности справедлива теорема.

Теорема.

Пусть функция W = f(Z) и W = q(Z) заданы на одном и том же множестве E и выполняются равенства , . Тогда справедливы равенства , . Если дополнительно известно, что B ≠ 0, то .