Правило дифференцирования

Так как формально определение производной функции комплексного переменного не отличается от определения производной вещественной (действительной) функции, то для производной функции комплексного переменного верны правила вычисления производных вещественных функций.

Например, справедливо правило:

1. Производная от константы равна 0 – ;

2. ;

3. ;

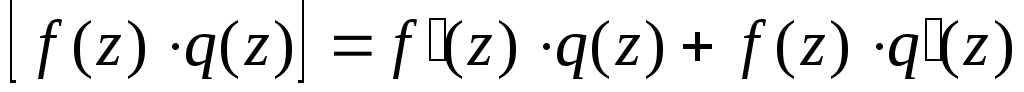4. , если q(Z) в этой точке не равняется 0;

5. , (в частности).

Производная сложной и обратной функций

Теорема.

Пусть функция W = f(Z) имеет в точке Z₀ производную , а функция имеет производную в точкеравную, тогда сложная функциятакже имеет в точкепроизводную и эта производная равна(чтобы множество значений функцииf(Z) не выходили за область определения функции ).

Теорема.

Пусть функция W = f(Z), отображающая множество E плоскости (Z) на область , имеет обратную функцию, и пусть выполняются условия:

• функция W = f(Z) имеет в точке Z₀ производную,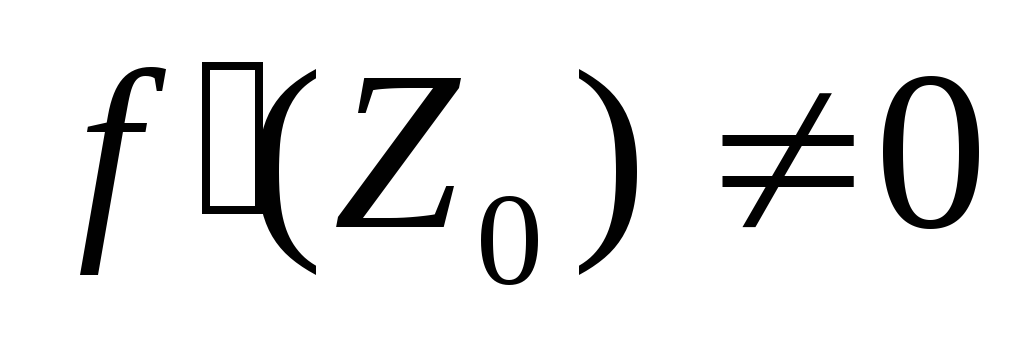

• функция непрерывна в точке,

тогда обратная функция имеет в точкепроизводную и эта производная равна.

Необходимые и достаточные условия дифференцируемости функции в точке

Функция u = u(x,y) называется дифференцируемой в точке , если ее полное приращениев этой точке, представляется в виде

(1),

где A, B – фиксированные числа, а величины – зависимые оти, стремящиеся к нулю, когда,, при этом всегда оказывается,.

Теорема.

Для того чтобы функция W = f(Z) имела в точке конечную производную , необходимо и достаточно, чтобы ее действительная и мнимая части u =u (x,y), v = v(x,y), были дифференцируемы соответственно в и, и чтобы в этой точке () выполнялись равенства

; (2),

(Коши-Римана, правильнее Даламбера-Эйлера).

Доказательство.

Необходимость. Пусть функция W = f(Z) имеет в точке Z₀ конечную производную . Покажем, что функцииu = u(x,y) и v = v(x,y) дифференцируемы в точке (), и что в этой точке выполняются равенства (2).

В силу существования производной имеет место представление(3), в котором величинапри.

Введем обозначения: ,, гдеизависят отии стремятся к нулю тогда, когда одновременно стремятся к нулюи. Таким образом, можно написать, что. Приравнивая здесь действительные и мнимые части. мы получаем, что

(4)

(5).

Так как при, то из (4), (5) следует, что функцииu и v дифференцируемы в u(), при этом в точке () ,, следовательно, выполняется условие Коши-Римана. Необходимость доказана.

Достаточность. Пусть вещественная и мнимая части u и v функции f(Z) дифференцируемы в точке (), и в этой точке выполняются равенства (2), покажем, что функция f(Z) имеет в точке конечную производную.

Введем обозначения. Пусть значения частных производных ,,,в точке() соответственно равны ,(так как выполняются равенства (2)). Тогда в силу дифференцируемости функцииu и v в точке () в этой точке будут иметь место представления

,

где величины ,,,, зависящие оти, стремятся к нулю, когда одновременно.

Таким образом,

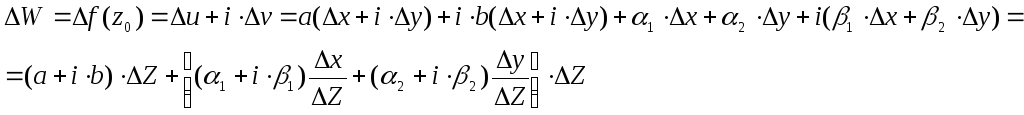Очевидно, модуль (). Так правая часть последнего неравенства стремится к нулю при одновременном стремлении к нулюи, то величина, когда.

Таким образом, в точке имеет место представление, где,, значит функцияW=f(Z) дифференцируема в точке Z₀ и ее производная . Достаточность установлена.

Так как функции ,являются непрерывно дифференцируемыми функциями, то сложные функцииитакже являются дифференцируемыми в точке().

Покажем, что в точке () выполняется условие (1).

Очевидно,

(так как ) и

.

Примеры.

Проверить условие Коши-Римана для функции

Проверить условие Коши-Римана для функции ().

Очевидно в полярных координатах . Поэтому

(выполняется)

.

Итак, эта функция является аналитической.

Отметим, что в полярных координатах производная комплексной функции вычисляется по формулам , где.