- •Лекция №1 Комплексные числа
- •Арифметические действия над комплексными числами
- •Алгебраическая форма записи комплексных чисел
- •Геометрические изображения комплексных чисел
- •Лекция №2 Тригонометрическая форма записи комплексного числа
- •Геометрическое истолкование суммы, разности, произведения и частного двух комплексных чисел
- •Корень n – ой степени из комплексного числа
- •Степень с произвольным рациональным показателем
- •Лекция №3 Предел последовательности комплексных чисел
- •Геометрическое истолкование предела последовательности комплексных чисел
- •Бесконечность и стереографическая проекция
- •Лекция №4 Ряды комплексных чисел
- •Абсолютно сходящиеся ряды комплексных чисел.
- •Основные понятия многочленов
- •Лекция №5 Понятие функции комплексного переменного.
- •Предел функции комплексного переменного
- •Непрерывность функции комплексного переменного
- •Лекция №6 Понятие равномерной непрерывности функции комплексной переменной
- •Понятие обобщенно непрерывной функции
- •Непрерывные кривые
- •Лекция №7 Понятие производной функции комплексного переменного
- •Формула для приращения функций.
- •Лекция №8 Дифференцируемость и дифференциал функции комплексного переменного
- •Правило дифференцирования
- •Производная сложной и обратной функций
- •Необходимые и достаточные условия дифференцируемости функции в точке
- •Лекция №9 Геометрический смысл определения производной функции комплексного переменного Геометрический смысл аргумента комплексно-значимой функции вещественной переменной
- •Геометрический смысл аргумента производной комплексной функции
- •Конформные отображения
- •Лекция №10 Геометрический смысл модуля производной
- •Пример (дробно-линейная функция)
- •Угол с вершиной в бесконечности или бесконечно удаленная точка
- •Лекция №11 Гармонические и сопряженные гармонические функции
- •Построение мнимой части аналитической функции по ее действительной части
- •Лекция №12 Элементарные аналитические функции
- •Точки, в которых нарушается конформное отображение
- •Лекция № 13 Свойства дробно-линейной функции Групповое свойство дробно-линейной функции
- •Лекция №14 Круговое свойство дробно-линейной функции.
- •Лекция №15 Образы областей, ограниченных прямой или окружность при дробно-линейном отображении
- •Неподвижные точки дробно-линейного отображения
- •Построение дробно-линейной функции, заданной в трех точках
- •Инвариантность двойного отношения при дробно-линейном преобразовании.
- •Отображение областей ограниченных прямыми илиокружностями.
- •Лекция №16 Показательная функция
- •Лекция №17 Тригонометрические функции cosZ, sinZ
- •Лекция №18 Гиперболические функции вещественного переменного.
- •Формулы приведения.
- •Лекция №19 Однозначные ветви многозначных функций.
- •Лекция №20 Логарифмы
- •Логарифмическая функция
- •Лекция №21 Степень с произвольным показателем
- •Общая степенная и показательная функция
- •Логарифм по произвольному основанию.
- •Понятие поверхности Римара
- •Лекция №22 Степенные ряды
- •Понятие верхнего предела вещественной числовой последовательности
- •Дифференцирование степенных рядов
- •Вопросы к экзамену по тфкп
- •Литература.
Лекция №22 Степенные ряды
Ряд
вида
![]() (1),
(1),
где Z0, c0, c1, … cn, ориентированные числа, а Z комплексная переменная называется степенным рядом.
Это простейший функциональный ряд, числами которого являются fn(Z)=cn(Z−Z0)n, числа c0, c1, … cn называются коэффициентами степенного ряда.
Этот ряд в отдельных точках может сходиться или расходиться.
Изучим структуру области сходимости и расходимости степенного ряда.
Понятие верхнего предела вещественной числовой последовательности
Рассмотрим вещественную числовую последовательность (an).
Число Λ называется верховым пределом последовательности, если выполняется следующее условия:
Для

 ,
тогда при всехn
> N
выполняется неравенство
,
тогда при всехn
> N
выполняется неравенство

Существует подпоследовательность
 .
.
Иначе говоря, верхним пределом называется самостоятельная прямая предельной точки этой последовательности.
Любая
числовая последовательность имеет
конечный и бесконечный верхний предел,
который обозначается символом
![]() .
.
Теорема Коши-Адамара.
Пусть
для степенного ряда
![]() (1) верхний предел
(1) верхний предел![]() (2) тогда:
(2) тогда:
Если
 ,
то ряд один абсолютно сходится во всей
конечной плоскости (Z).
,
то ряд один абсолютно сходится во всей
конечной плоскости (Z).
Если
 ,
то степенной ряд (1) сходится в точкеZ
= Z0
и расходится во всех точках
,
то степенной ряд (1) сходится в точкеZ
= Z0
и расходится во всех точках
 .
.Если
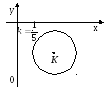
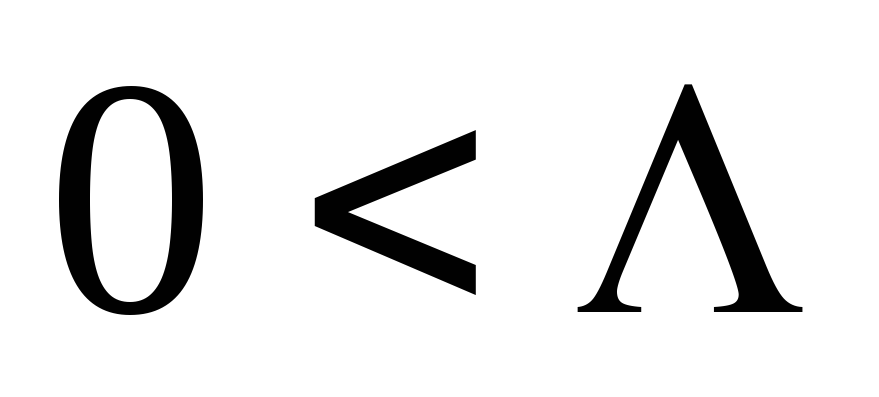 ,
то степенной ряд (1) абсолютно сходится
в любой точкеZ
круга
,
то степенной ряд (1) абсолютно сходится
в любой точкеZ
круга
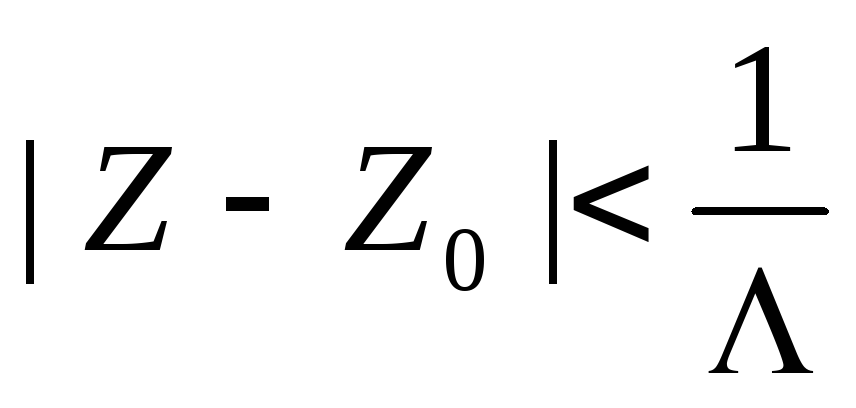 и расходится в любой его точке Z
круга
и расходится в любой его точке Z
круга
 .
.
Доказательство.
Пусть
 ,
тогда в силу (2) будет также
,
тогда в силу (2) будет также (
( ).
).
Поэтому
для любой фиксированной точки Z
будет
![]() ,
следовательно, по признаку Коши ряд (1)
абсолютно сходится в любой точкеZ.
,
следовательно, по признаку Коши ряд (1)
абсолютно сходится в любой точкеZ.
Пусть теперь
 .
Покажем, что ряд (1) расходится в любой
точке
.
Покажем, что ряд (1) расходится в любой
точке
 .
Легко видеть, что некоторая
последовательность
.
Легко видеть, что некоторая
последовательность
 .
Значит для любого
.
Значит для любого

 и тем более
и тем более
Следовательно
для ряда (1) в точке
![]() не выполняется необходимый признак
сходимости ряда (общий член не стремится
к нулю при n→∞),
поэтому ряд один в этой точке расходится.
не выполняется необходимый признак
сходимости ряда (общий член не стремится
к нулю при n→∞),
поэтому ряд один в этой точке расходится.
Сходимость ряда (1) в точке Z = Z0 очевидна, т. к. в этой точке все члены ряда (1), начиная со 2, обращаются в нуль.
Пусть теперь 0 < Λ < +∞. Покажем, что ряд (1) абсолютно сходится в любой точке Z круга
 .
Сходимость ряда (1) в точке
Z
= Z0
очевидна. Возьмем любое
.
Сходимость ряда (1) в точке
Z
= Z0
очевидна. Возьмем любое
 из круга
из круга
 .
Очевидно,
.
Очевидно,
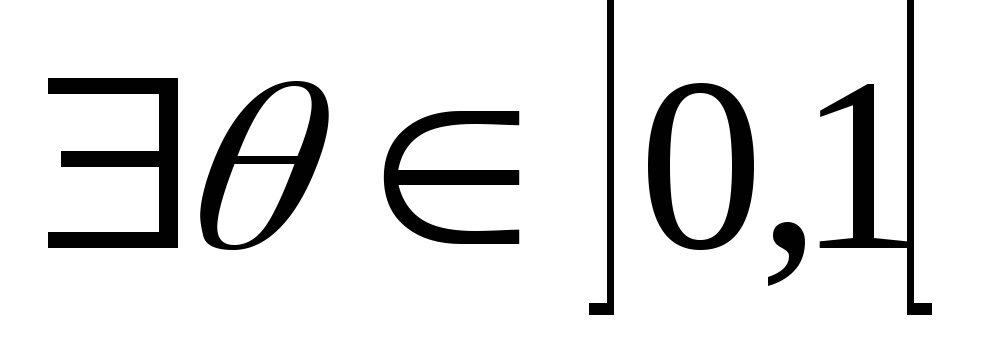 такое что, будет выполняться
такое что, будет выполняться
 .
.
Рассмотрим
число
![]() .
По определению верхнего предела
существует числоN
= N(
.
По определению верхнего предела
существует числоN
= N(![]() ),
такое, что при всех n
> N
будет выполняться неравенство
),
такое, что при всех n
> N
будет выполняться неравенство
![]() .
При этих номерахn
> N
будет
.
При этих номерахn
> N
будет
![]() .
.
Следовательно, в силу признака Коши (непредельная форма), ряд (1) в точке Z будет абсолютно сходиться.
Докажем
теперь, что ряд (1) расходится в любой
точке Z
внешности круга
![]() .
.
Очевидно,
существует такое число
![]() ,
что будет выполняться равенство
,
что будет выполняться равенство
![]() .
По определению верхнего предела
существует подпоследовательность
.
По определению верхнего предела
существует подпоследовательность
![]() ,
значит будет выполняться
,
значит будет выполняться![]() ,
,![]() ,
поэтому в точкеZ
для ряда (1) не выполняется необходимое
условие сходимости. Ряд в этой точке
расходится.
,
поэтому в точкеZ
для ряда (1) не выполняется необходимое
условие сходимости. Ряд в этой точке
расходится.
Из
теоремы Коши-Адамара вытекает. Что для
любого степенного ряда (1) существует
число
![]() ,
такое что, во всех числахZ
круга |Z
- Z0|
< R
ряд (1) абсолютно сходится, а во всех
точках внешности этого круга |Z
- Z0|
> R
ряд расходится.
,
такое что, во всех числахZ
круга |Z
- Z0|
< R
ряд (1) абсолютно сходится, а во всех
точках внешности этого круга |Z
- Z0|
> R
ряд расходится.
Такой круг |Z - Z0| < R называется кругом сходимости степенного ряда (1).

Число R при этом называется радиусом сходимости степенного ряда.
Очевидно,
![]() .
.
Радиус
окружности можно вычислить по формулам
![]() ,
если эти пределы существуют.
,
если эти пределы существуют.
Из теоремы Коши-Адамара в частности вытекает первая теорема Абеля.
Теорема Абеля
Если
степенной ряд
![]() (1) сходится в некоторой точке
(1) сходится в некоторой точке
![]() ,
то абсолютно сходится в любой точке
круга |Z
- Z0|
< |Z1
- Z0|.
,
то абсолютно сходится в любой точке
круга |Z
- Z0|
< |Z1
- Z0|.

Доказательство.
Т.
к. ряд (1) сходится в точке Z1,
то эта точка Z1
не лежит во внешности круга сходимости.
Поэтому эта точка Z1
либо лежит
внутри круга сходимости, либо на его
границе. Но тогда круг |Z-Z0|
< |Z1-Z0|
будет целиком содержаться в круге
сходимости степенного ряда |Z-Z0|
< R
(т.к. |Z-Z0|
![]() R)
и потому ряд (1) во всех точках,
рассматриваемого круга, абсолютно
сходится.
R)
и потому ряд (1) во всех точках,
рассматриваемого круга, абсолютно
сходится.
Пример.
Найти радиус и круга сходимости степенного ряда.
![]()
Очевидно, cn = 5n+n
Поэтому![]()
Кругом
сходимости будет
![]()