Лекция №11 Гармонические и сопряженные гармонические функции

Дважды непрерывно дифференцируемая функция называетсягармонической в области D плоскости (Z), если во всех точках этой области выполняется равенство

(6).

Отметим, что уравнение (6) называют уравнением Лапласа и коротко записывают

(7).

Две функции u(x,y) и v(x,y) области D плоскости (Z) называются сопряженными гармоническими функциями в этой области, если во всех точках этой области выполняются условия Коши-Римана ,.

Мы покажем, что действительная и мнимая части u(x,y), v(x,y) в аналитической области D функции W = f(Z) являются сопряженными гармоническими функциями. Так как у аналитической функции действительная и мнимая части удовлетворяют условиям Коши-Римана, то нам достаточно доказать гармоничность функций u(x, y), v(x, y) в области D.

Отметим, что аналитическая в области D функция f(Z) имеет производную всех порядков (без доказательства). Поэтому действительная и мнимая части этой функции имеют в области D производные всех порядков по всем переменным, и эти производные непрерывны. Поэтому в частности будут существовать все непрерывные производные 1^го и 2^го порядка. То есть эти функции будут дважды непрерывно дифференцируемы.

Воспользуемся теперь условием Коши-Римана ,.

Продифференцируем первое равенство по x, а второе – по y, и сложим. Получим (так как смешанные производные, когда непрерывны, равны). Следовательно,u-гармоническая функция, аналогично доказывается, что v гармоническая функция, следовательно, u и v – сопряженные гармонические функции.

Построение мнимой части аналитической функции по ее действительной части

Пусть в некоторой области D плоскости известна действительная часть u(x,y) аналитической функции. Требуется построить ее мнимую часть v(x,y) в этой области. Как мы знаем ;.

Составим выражение . Очевидно,, так как(Лапласиян). Следовательно, выражение будет полным дифференциалом некоторой функции.

Пусть D – это односвязная область, тогда криволинейный интеграл не будет зависеть от формы и пути, соединяющего точки () и (x,y), принадлежащие D (лежащие в D) и, следовательно, будет представлять собой некоторую функцию верхнего предела. Как мы знаем из теории криволинейных интегралов, эта функция дифференцируема в областиD, и ее частные производные исоответственно равныp(x,y), Q(x,y). Следовательно, в области D частные производные функций v(x,y) и совпадают. Поэтому эти функции могут отличаться лишь на константу, следовательно,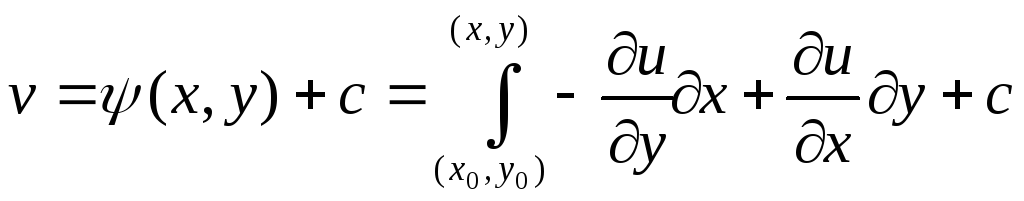. Как видно, мнимая часть аналитической функции определяется с точностью до постоянной.

Отметим, что, если известно значение аналитической функции W = f(Z) в какой-нибудь одной точке (), то мнимая частьv(x,y) этой функции и, следовательно, сама аналитическая функция f(Z) определяется однозначно по действительной части u(x,y).

В случае многосвязной области D криволинейный интегралпредставляет многозначную функцию. Поэтому мнимая частьv(x,y) будет также, вообще говоря, многозначной функцией. Действительная часть по мнимой части строится аналогичным образом.

Отметим, что мнимая часть v(x,y) функции является действительной частью функции. Отметим, что мнимая часть по действительной находится другим способом. Пишут уравнения;. Интегрируют одно из равенств (первое поx)

(1), затем дифференцируют полученное равенство по переменной y . Отсюда находяти подставляют его в (1).

Пример.

Построить мнимую часть числа по действительной

;

. Интегрируем по x.

. Находим производную по y и приравниваем

, и теперь интегрируем .

Таким образом,

, ,,, следовательно,;

.