Формулы приведения.

Из равенств

непосредственно вытекают формулы приведения, аналогичные функциям приведения для вещественных функций sinx и cosx.

Докажем, например, что справедливы равенства:

В самом деле, полагая, что Z₁ = Z, а Z₂ = мы получаем:

Аналогично выводятся остальные формулы приведения.

Лекция №19 Однозначные ветви многозначных функций.

Пусть функция W = f(Z) отображает множество , на множество, тогда функцияZ = φ(W), отображающая множество D на множество E, которая ставит в соответствие точкеее полный прообраз при отображенииW = f(Z), т. е. все такие , в которыхf(Z) = W, называется обратной функцией.

Обратные функции комплексного переменного для однозначных функций W=f(Z), как правило, являются многозначными.

Например, для функции W = Zⁿ обратная функция являетсяn-значной, а для функции W = e^Z обратная функция Z = lnW будет бесконечно-значной.

С целью изучения многозначной функции при помощи разработанного аппарата для однозначных функций выделяют однозначные ветви. Это осуществляется по следующей схеме:

Пусть в области g(W) нам задана однозначная обобщенно непрерывная функция Z = f(W). Как известно, образ G(Z) области g будет также областью.

Пусть область g каким-то образом удалось разбить на конечное или счетное число попарно не пересекающихся областей g_k, обладающих свойствами:

1. точки (W)либо принадлежащей только какой-то одной областиg_k, либо являющейся граничной точкой нескольких областей g_k.

2. Функция Z = f(W) переводит две различные точки (W₁) и (W₂) g_k в различные точки, т. е. отображение является взаимно однозначным.

Легко видеть, что образами областей g_k(W) при отображении Z = f(W) будут и области G_k(Z), причем граничные точки областей g_k, которые принадлежат g, будут отображаться в граничные точки областей G_k.

Легко видеть, что отображение Z = f(W) области g_k будет взаимнооднозначным. Поэтому существует однозначная обратная функция W=F_k(Z), отображающая уже G_k на g_k. При различных k мы получаем различные обратные функции.

Эти однозначные обратные функции и называются ветвями обратной функции W = F(Z), отображающей множество G на множество g.

Эти ветви получаются следующим образом из обратной функции W = F(Z). Значения функции W = F(Z) на G_k ограничиваются тем, что принадлежат области g_k.

Z=f(W) задана на g(W), обратная функция W=F(Z) задана на множестве G=f(g) плоскости (Z) (это многозначная функция).

Область g разбили на части g₁, g₂, … ,g_n, образы их будут областью G_k для g.

Существует функция W=F_k(Z), однозначная ветвь обратной функции W=F(Z), значение функции W=F(Z) ограничиваются тем…

Как видно, характер областей G_k(Z) и, следовательно, характер однозначных ветвей W = F_k(Z) существенно зависит от способа разбиения области g(W) на области g_k.

Отметим, что в прошедших случаях удается разбить область g плоскости (W) на части g_k таким образом, что все их образы G_k будут совпадать между собой. Обозначим их через . Тогда на одном и том же множествеопределятся однозначные ветвиW = F_k(Z).

Приведенный способ выделения однозначных ветвей из многозначной функции, вообще говоря, не применим к произвольным обобщенно непрерывным функциям Z = f(W), но он всегда применим к аналогичным функциям Z = f(W) в области g(W), за исключением изолированных точек, в которых функция обращается в бесконечность.

Аналитическая функция Z = f(W) называется однолистной в области g(W), если она принимает различные значения в различных точках множества g, т.е. является инъективной.

Если же функция Z = f(W) принимает одно и тоже значения в некоторых точках области g(W), то она называется многолистной.

Выше мы разбиваем область g(W) на области одномерности g_k, в которой она была однолистной. Таким образом, выделение однозначных ветвей многозначной функции сводится к разбиению многолистной области g(W) функции Z = f(W) на области однолистности g₁, g₂, …

Пример.

Функция W = (1) (Это то же W = F(Z)). Эта функция является n-значной в точкеZ 0 и ∞ она принимает n значений

(2),

которые располагаются в вершинах правильного n-угольника с центром в нуле.

Очевидно, функция (1) является обратной для аналитической функции

Z=Wⁿ (3).

Функция (3) принимает равные значения во всех точках (2), следовательно, эта функция является n-мерной.

Т. к. функция (3) принимает равные значения в вершинах правильного n-угольника плоскости (W) с центром в нуле (0), то область однолистности не должна содержать ни одной пары таких точек. Наиболее простой областью одномерности функции (3) является внутренность угла раствора с вершиной в нуле.

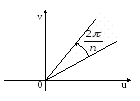
Следовательно, n-листная плоскость (W) допускает разбиение на n-однолистных областей g_k, являющиеся углами, которые образуют между собой лучи, выходящие из нуля, под углами кратными друг к другу.

Пусть эти лучи составляют с действительной осью и углы

Очевидно, функция (3) отобразит эти лучи в один луч, который составляет с осью x-ов угол:

А область g_k отобразится на область , ограниченную этим лучом.

Будем рассматривать функцию (1) на области ограничивая тем, что ее значение принадлежат некоторой областиg_k. Тогда мы получим n однозначных ветвей, которые будем обозначать соответственно.