Лекция №17 Тригонометрические функции cosZ, sinZ

формулы Эйлера.

Правые части этих формул определены для комплексногои является аналитическими функциями, поэтому естественноcosZ определяется по формуле:

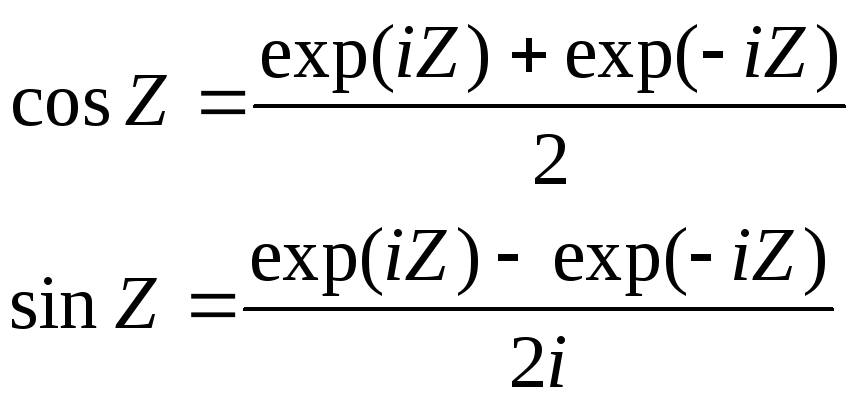(2)

Рассмотрим свойства тригонометрических функций:

1. cosZ - четная функция,

sinZ - нечетная функция

Действительно,

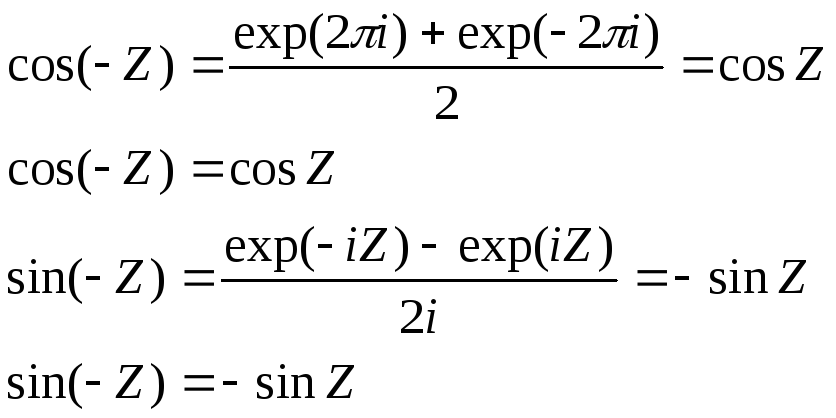
2. Косинус Z и синус Z (cosZ, sinZ),периодические функции с периодом 2π , т. е. при замене Z на 2π аргументы показательной функции в правых частях изменяются на ±2π ,т.е. есть периоды показательной функции.

Покажем, что 2π есть основной период функции cosZ и sinZ. Пусть w есть период cosZ, тогда cos(Z+w)=cosZ (по определению периода) при получим:

,тогда

это можно записать:

По формуле (1) (Z=i(gw+)), т. к. cosw = cos0 = 1

Следовательно, k принимает четные значения, т.е. период w = 2π, поэтому 2π - основной период.

3. Теорема сложения.

Справедливы формулы:

cos(Z₁+Z₂)=cosZ₁∙cosZ₂-sinZ₁∙sinZ₂

sin(Z₁+Z₂)=sinZ₁∙cosZ₂+cosZ₁∙sinZ₂

Доказательство.

Чтобы доказать справедливость этих формул, сначала этого выделим формулу Эйлера. Для этого умножим обе части второй формулы равенства(2) на i: .

Складываем первую формулу с полученной:

cosZ+i∙sinZ=exp(iZ) (формула Эйлера), Z заменим на Z₁+Z₂.

(4)

Вместо Z₁ и Z₂ мы поставим (-Z₁) и (-Z₂).

(5)

Складывая и вычитая (4) и (5), получим

(6)

Пусть теперь Z₁ = Z и Z₂ = -Z, подставим и получим

1 = cos²Z+sin²Z

(cos(Z-Z)=cosZ∙cosZ+sinZ∙sinZ).

С тригонометрическими функциями cosZ и sinZ тесно связаны гиперболические функции: chZ - гиперболический косинус Z и shZ - гиперболический синус Z.

(7)

chZ = cos(iZ); shZ = -i∙sin(iZ)

Определим действительные и мнимые части функций cosZ и sinZ.

Пусть Z = x+i∙y

действительная часть

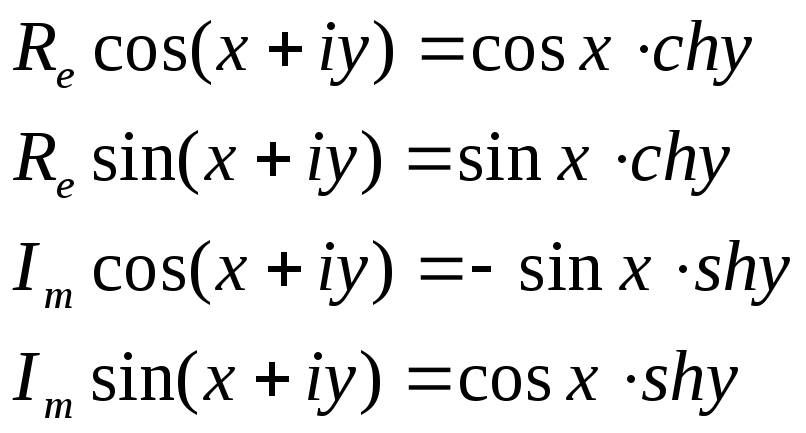
Она ввела функции cosZ и sinZ, используя формулы:

;

Поясним откуда взялись эти формулы:

(1)

y заменим на –y

(2)

Сложим и разделим на два: , если из (1) вычели (2) и разделим на2i, то получим: (ну аy можно заменить на x).

Вывели равенства:

(*)

Т. к.

Подставим вместо Z точку iZ :

(умножим числитель и знаменатель на i).

ch²Z - sh²Z = 1 (возведем (*) в квадрат).

Отделим действительную и мнимую части:

Найдем модули функций cosZ и sinZ. Очевидно,

(8)

(9)

Из формул (8) и (9) непосредственно вытекает, что:

(заменим в (8) sin²x на 1, отбросим в (9) sin²x)

(10)

(отбросим в (8) sin²x, заменим в (9) sin²x на 1)

(11)

()

Лекция №18 Гиперболические функции вещественного переменного.

Вещественные гиперболические функции shx и chx определяются функциями: ,

Эти функции заданы на всей числовой оси.

Очевидно, shx нечетна (sh(-x) = -sh(x)), функция chx четная (ch(-x) = chx) (из выше записанных функций).

Следовательно, график функции shx симметричен относительно начала координат, а chx симметричен относительно оси y.

При возрастании x от -∞ до +∞ функция shx возрастает от -∞ до +∞, обращаясь в нуле в 0.

sh0 = 0

Функция chx при возрастании х от -∞ до +∞ убывает от +∞ до 1. При дальнейшем же возрастании х от 0 до +∞, функция chx возрастает от 1 до

+∞.

Из формул для shx и chx непосредственно следует, что разность

chx - shx = e^-x > 0

сh²x - sin²x = 1.

Следовательно, графики этих функций имеют вид, указанный на чертеже.

Из функции (10) и (11) следует, что модули функции |cosZ| и |sinZ| стремятся в бесконечность, когда |y| → ∞.

Из тех же функций следует, что cosZ и sinZ смогут обратиться в нуль лишь на действительной оси, т. е. когда y = 0. По вещественной оси cosZ=cosx; sinZ=sinx. Следовательно, функции cosZ и sinZ обращаются в нуль соответственно только в точках (cosZ) и (sinZ)

Вычислим производную от cosZ и sinZ. Очевидно:

Следовательно, функции W = cosZ и W = sinZ являются аналитическими функциями и они осуществляют конформные отображения во всех точках, за исключением соответствующих точек и(т. к. в них производная обращается в нуль).

Пример (конформного отображения c плоскостью показательной функции).

Отобразить конформную полосу ограниченную прямыми y = 0 и y = на верхнюю полость.

Произведем отображение W₁ = e^Z. Оно приведет прямую y = 0 в луч (1), а прямуюy = в луч (2).

Теперь произведем отображение W = W₁³, это отображение переведет лучи (1) и (2) в лучи ,.

Следовательно, функция W = e^3Z и будет искомым отображением.