
- •Лекция №1 Комплексные числа
- •Арифметические действия над комплексными числами
- •Алгебраическая форма записи комплексных чисел
- •Геометрические изображения комплексных чисел
- •Лекция №2 Тригонометрическая форма записи комплексного числа
- •Геометрическое истолкование суммы, разности, произведения и частного двух комплексных чисел
- •Корень n – ой степени из комплексного числа
- •Степень с произвольным рациональным показателем
- •Лекция №3 Предел последовательности комплексных чисел
- •Геометрическое истолкование предела последовательности комплексных чисел
- •Бесконечность и стереографическая проекция
- •Лекция №4 Ряды комплексных чисел
- •Абсолютно сходящиеся ряды комплексных чисел.
- •Основные понятия многочленов
- •Лекция №5 Понятие функции комплексного переменного.
- •Предел функции комплексного переменного
- •Непрерывность функции комплексного переменного
- •Лекция №6 Понятие равномерной непрерывности функции комплексной переменной
- •Понятие обобщенно непрерывной функции
- •Непрерывные кривые
- •Лекция №7 Понятие производной функции комплексного переменного
- •Формула для приращения функций.
- •Лекция №8 Дифференцируемость и дифференциал функции комплексного переменного
- •Правило дифференцирования
- •Производная сложной и обратной функций
- •Необходимые и достаточные условия дифференцируемости функции в точке
- •Лекция №9 Геометрический смысл определения производной функции комплексного переменного Геометрический смысл аргумента комплексно-значимой функции вещественной переменной
- •Геометрический смысл аргумента производной комплексной функции
- •Конформные отображения
- •Лекция №10 Геометрический смысл модуля производной
- •Пример (дробно-линейная функция)
- •Угол с вершиной в бесконечности или бесконечно удаленная точка
- •Лекция №11 Гармонические и сопряженные гармонические функции
- •Построение мнимой части аналитической функции по ее действительной части
- •Лекция №12 Элементарные аналитические функции
- •Точки, в которых нарушается конформное отображение
- •Лекция № 13 Свойства дробно-линейной функции Групповое свойство дробно-линейной функции
- •Лекция №14 Круговое свойство дробно-линейной функции.
- •Лекция №15 Образы областей, ограниченных прямой или окружность при дробно-линейном отображении
- •Неподвижные точки дробно-линейного отображения
- •Построение дробно-линейной функции, заданной в трех точках
- •Инвариантность двойного отношения при дробно-линейном преобразовании.
- •Отображение областей ограниченных прямыми илиокружностями.
- •Лекция №16 Показательная функция
- •Лекция №17 Тригонометрические функции cosZ, sinZ
- •Лекция №18 Гиперболические функции вещественного переменного.
- •Формулы приведения.
- •Лекция №19 Однозначные ветви многозначных функций.
- •Лекция №20 Логарифмы
- •Логарифмическая функция
- •Лекция №21 Степень с произвольным показателем
- •Общая степенная и показательная функция
- •Логарифм по произвольному основанию.
- •Понятие поверхности Римара
- •Лекция №22 Степенные ряды
- •Понятие верхнего предела вещественной числовой последовательности
- •Дифференцирование степенных рядов
- •Вопросы к экзамену по тфкп
- •Литература.
Лекция №9 Геометрический смысл определения производной функции комплексного переменного Геометрический смысл аргумента комплексно-значимой функции вещественной переменной
Рассмотрим
комплексно-значимую функцию вещественной
переменной
![]() ,
,![]() .
Пусть эта функция в некоторой точке
.
Пусть эта функция в некоторой точке![]() имеет производную
имеет производную![]() (так как аргумент0
и
(так как аргумент0
и
![]() не определен).
не определен).
Выясним
геометрический смысл аргумента
![]() .
.

Рассмотрим
в плоскости
(Z)
две точки
![]() (
(![]() )
и
)
и
![]() на кривой
на кривой![]() .
Проведем
.
Проведем
через
эти две точки секущую. Очевидно, вектор
![]() (
(![]() )–
)–![]() коллинеарен этой секущей. Значит,
отношение
коллинеарен этой секущей. Значит,
отношение![]() так же этот вектор будет коллинеарен
секущей. Вычислим предел,
так же этот вектор будет коллинеарен
секущей. Вычислим предел,![]() ,
поэтому
,
поэтому
![]() (2)
(2)
(Этот
предел не в обычном смысле, то есть из
![]() можно извлечь такие представители,
которые будут сходится к одному из
представителей
можно извлечь такие представители,
которые будут сходится к одному из
представителей![]() ).
).
Так
как касательная – это есть предельное
положение секущей, то из равенства (2)
следует, что
![]() – это есть угол, который составляет
касательная к кривой
– это есть угол, который составляет
касательная к кривой![]() в точке
в точке![]() с действительной осью.
с действительной осью.
Геометрический смысл аргумента производной комплексной функции
Пусть
функция W
= f(Z)
имеет
в точке
![]() конечную производную
конечную производную![]() ,
вычислим геометрический смысл
,
вычислим геометрический смысл![]() .
С этой целью выпустим из точки
.
С этой целью выпустим из точки![]() кривую
кривую![]() ,
такую что производная
,
такую что производная![]() и существует.
и существует.

Отображение
W=f(Z)
переведет эту кривую L
в новую кривую
![]() ,
выходящую из точки
,
выходящую из точки![]() (T
и
(T
и
![]() касательные).
касательные).
Покажем,
что кривая
![]() (лямбда),
заданная уравнением
(лямбда),
заданная уравнением![]() тоже имеет в точке
тоже имеет в точке![]() касательную. Очевидно,
касательную. Очевидно,![]() ,
значит
,
значит![]() (3).
(3).
Таким
образом, кривая
![]() имеет в точке
имеет в точке![]() касательную, которая составляет с
действительной осью угол равный величине
(3). Из равенства (3) следует, что
касательную, которая составляет с
действительной осью угол равный величине
(3). Из равенства (3) следует, что
![]() (4).
(4).
Следовательно,
![]() – это есть угол, на который поворачивается
касательная к кривойL
в
рассматриваемой точке Z0
при отображении W=f(Z).
Нетрудно видеть, что угол поворота
касательной к кривой
– это есть угол, на который поворачивается
касательная к кривойL
в
рассматриваемой точке Z0
при отображении W=f(Z).
Нетрудно видеть, что угол поворота
касательной к кривой
![]() в точкеZ0
при отображении W
= f(Z)
не зависит от выбора этой кривой.
в точкеZ0
при отображении W
= f(Z)
не зависит от выбора этой кривой.
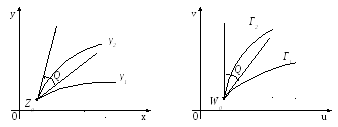
Если
мы возьмем в плоскости
(Z)
две кривые
![]() и
и![]() ,
образующие в точкеZ0
некоторый угол Q.
,
образующие в точкеZ0
некоторый угол Q.

То
при отображении W
= f(Z)
эти две кривые перейдут в новые кривые
![]() и
и![]() плоскости(W),
которые в точке
плоскости(W),
которые в точке
![]() также
будут образовывать угол Q,
так как касательные к
также
будут образовывать угол Q,
так как касательные к
![]() и
и![]() в точке
в точке![]() получаются путем поворота касательных
к
получаются путем поворота касательных
к![]() и
и![]() в точке
в точке![]() на один и тот же угол, равный
на один и тот же угол, равный![]() .
.
Конформные отображения
Отображение, осуществляемое посредством непрерывной функции W = f(Z), называется конформным в точке Z0, если оно сохраняет углы между кривыми, выходящими из точки Z0.
Если при этом отображении сохраняется не только величина угла между кривыми, но и направление отсчета, то говорят о конформном отображении 1го рода.
Если же при отображении W = f(Z) величина углов между кривыми сохраняется, а направление их отсчета меняется на противоположное, то говорят о конформном отображении 2го рода.
Из
геометрического смысла аргумента
производной непосредственно следует,
что аналитические функции W
= f(Z)
в точках Z0,
где
![]() ,
осуществляют конформное отображение
1го
рода.
,
осуществляют конформное отображение
1го
рода.
Покажем, что функции, сопряженные аналитическим, осуществляют конформные отображения 2го рода.
Рассмотрим
функцию
![]() ,
из чертежа непосредственно видно, что
функция
,
из чертежа непосредственно видно, что
функция![]() осуществляет конформное отображение
2го
рода в любой точке
осуществляет конформное отображение
2го
рода в любой точке
![]() .
.

Рассмотрим
аналитическую функцию f(Z),
которая в точке Z0
имеет производную
![]() .
Построим отображение
.
Построим отображение![]() ,
покажем, что оно в точкеZ0
конформное отображение 2го
рода. Очевидно, отображение
,
покажем, что оно в точкеZ0
конформное отображение 2го
рода. Очевидно, отображение
![]() представляется в виде произведения
двух отображений
представляется в виде произведения
двух отображений![]() ;
;![]() .
Как мы знаем, функция
.
Как мы знаем, функция![]() осуществляет в точкеZ0
конформное отображение 1го
рода. Возьмем в плоскости
(Z)
две кривые, исходящие из точки Z0
и составляющие между собой угол Q.
осуществляет в точкеZ0
конформное отображение 1го
рода. Возьмем в плоскости
(Z)
две кривые, исходящие из точки Z0
и составляющие между собой угол Q.
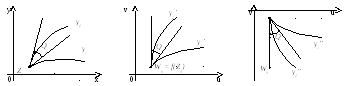
При
отображении
![]() эти кривые перейдут в кривые
эти кривые перейдут в кривые![]() и
и![]() ,
которые также будут образовывать между
собой уголQ,
причем направление отсчета углов
сохраняется. Произведем теперь отображение
,
которые также будут образовывать между
собой уголQ,
причем направление отсчета углов
сохраняется. Произведем теперь отображение
![]() .
Оно является конформным2го
рода. Поэтому кривые
.
Оно является конформным2го
рода. Поэтому кривые
![]() и
и![]() перейдут в кривые
перейдут в кривые![]() и
и![]() ,
угол между которыми в точке
,
угол между которыми в точке![]() сохраняются, но направление изменится
на противоположное. Следовательно,
отображение
сохраняются, но направление изменится
на противоположное. Следовательно,
отображение![]() переведет кривые
переведет кривые![]() ,
,![]() в кривые
в кривые![]() ,
,![]() ,
угол между которыми сохраняется, но
направление изменяется на противоположное.
Следовательно, отображение
,
угол между которыми сохраняется, но
направление изменяется на противоположное.
Следовательно, отображение![]() конформное 2го
рода.
конформное 2го
рода.
