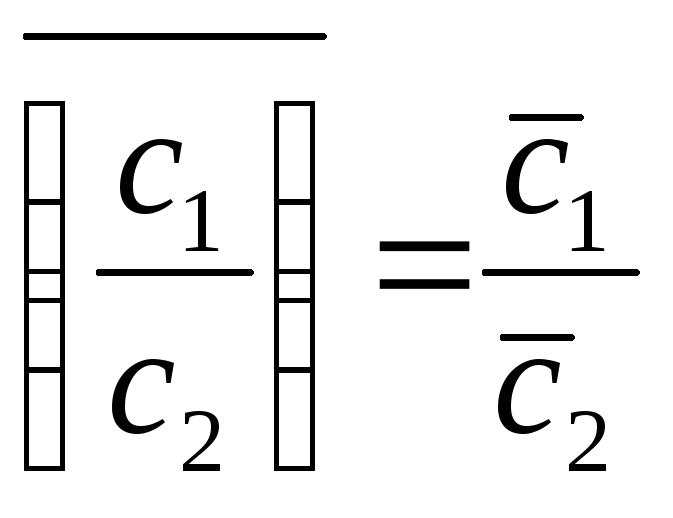Оглавление

Лекция №1 4

Комплексные числа 4

Арифметические действия над комплексными числами 4

Алгебраическая форма записи комплексных чисел 5

Геометрические изображения комплексных чисел 6

Лекция №2 8

Тригонометрическая форма записи комплексного числа 8

Геометрическое истолкование суммы, разности, произведения и частного двух комплексных чисел 8

Корень n – ой степени из комплексного числа 11

Степень с произвольным рациональным показателем 12

Лекция №3 12

Предел последовательности комплексных чисел 12

Геометрическое истолкование предела последовательности комплексных чисел 14

Бесконечность и стереографическая проекция 14

Лекция №4 17

Ряды комплексных чисел 17

Абсолютно сходящиеся ряды комплексных чисел. 18

Основные понятия многочленов 20

Лекция №5 23

Понятие функции комплексного переменного. 23

Предел функции комплексного переменного 24

Непрерывность функции комплексного переменного 26

Лекция №6 27

Понятие равномерной непрерывности функции комплексной переменной 27

Понятие обобщенно непрерывной функции 27

Непрерывные кривые 28

Лекция №7 30

Понятие производной функции комплексного переменного 30

Формула для приращения функций. 32

Лекция №8 33

Дифференцируемость и дифференциал функции комплексного переменного 33

Правило дифференцирования 34

Производная сложной и обратной функций 34

Необходимые и достаточные условия дифференцируемости функции в точке 34

Лекция №9 37

Геометрический смысл определения производной функции комплексного переменного 37

Геометрический смысл аргумента производной комплексной функции 38

Конформные отображения 40

Лекция №10 42

Геометрический смысл модуля производной 42

Пример (дробно-линейная функция) 42

Угол с вершиной в бесконечности или бесконечно удаленная точка 44

Лекция №11 46

Гармонические и сопряженные гармонические функции 46

Построение мнимой части аналитической функции по ее действительной части 47

Лекция №12 49

Элементарные аналитические функции 49

Точки, в которых нарушается конформное отображение 50

Лекция № 13 54

Свойства дробно-линейной функции 54

Групповое свойство дробно-линейной функции 54

Лекция №14 58

Круговое свойство дробно-линейной функции. 58

Лекция №15 60

Образы областей, ограниченных прямой или окружность при дробно-линейном отображении 60

Неподвижные точки дробно-линейного отображения 61

Построение дробно-линейной функции, заданной в трех точках 62

Инвариантность двойного отношения при дробно-линейном преобразовании. 63

Отображение областей ограниченных прямыми или окружностями. 64

Лекция №16 66

Показательная функция 66

Лекция №17 71

Тригонометрические функции cosZ, sinZ 71

Лекция №18 75

Гиперболические функции вещественного переменного. 75

Формулы приведения. 77

Лекция №19 78

Однозначные ветви многозначных функций. 78

Лекция №20 81

Логарифмы 81

Логарифмическая функция 83

Лекция №21 84

Степень с произвольным показателем 84

Общая степенная и показательная функция 85

Логарифм по произвольному основанию. 85

Понятие поверхности Римара 86

Лекция №22 88

Степенные ряды 88

Понятие верхнего предела вещественной числовой последовательности 88

Дифференцирование степенных рядов 91

Вопросы к экзамену по ТФКП 95

Литература. 97

Лекция №1 Комплексные числа

Комплексным числом C называется упорядоченная пара (a,b) вещественных чисел a и b.

Числа вида (a,0) мы будем отождествлять с вещественным числом a.

Теорема.

Множество вещественных чисел составляет часть множества комплексных чисел.

Число a называется вещественной частью комплексного числа . ПишутReC = a.

Число b называется мнимой частью комплексного числа , и обозначаетсяImC = b.

Если b ≠ 0, то комплексное число называетсямнимым числом. Если же b ≠ 0 и, кроме того, а = 0, то комплексное число называетсячисто мнимым числом.

Два комплексных числа исчитаются равными(с₁ = с₂), если а₁ = а₂ и b₁ = b₂ (равны их вещественные и мнимые части чисел).

Арифметические действия над комплексными числами

Под суммой двух комплексных чисел ипонимается комплексное числос = (а₁+ а₂, b₁+b₂) и обозначается с = с₁+с₂ .

Вычитание определяется как действие обратное сложению.

Под разностью двух комплексных чисел ипонимается комплексное числос, такое что с₁ = с+с₂ и обозначается с = с₁-с₂. Оказывается, что эта разность единственная и притом равна .

Произведением двух комплексных чисел иназывается комплексное числос равное . Действие деления определяется как обратное умножению.

Под частным двух комплексных чисел ипонимается комплексное число, такое чтос₁ = с·с₂ . Частное обозначается символом с = с₁/c₂ . Оказывается, что частное существует и единственно, если с₂ ≠ 0 (c₁/0 = c; c₁ = 0·с = 0; 0/0 = c; 0 = 0·с).

Действия сложения и умножения комплексных чисел обладают обычными арифметическими свойствами:

• с₁ + (с₂ + с₃) = (с₁ +с₂) + с₃ (ассоциативность сложения)

• с₁ · (с₂ · с₃) = (с₁ · с₂) · с₃ (ассоциативность умножения)

• с₁ + с₂ = с₂ + с₁ (коммутативность сложения)

• с₁ · с₂ = с₂ · с₁ (коммутативность умножения)

• с₁ · (с₂ + с₃) = с₁ · с₂ + с₁ · с₃ (дистрибутивность умножения относительно операции сложения)

Среди комплексных чисел выделяют число (0,1), которое обозначается символом i. Это число обладает характеристическим свойством:

i² = i·i = -1

Действительно i·i = (0,1)·(0,1) = (0·0-1·1, 0·1+1·0) = (-1,0) = -1

Часто пишут неправильно, что . На самом деле -.

Алгебраическая форма записи комплексных чисел

Легко видеть, что произведение b·i = (b,0)·(0,1) = (b·0–0·1, b·1+0·0) = (0,b) и c=(a,b)=(a,0)+(0,b). Поэтому c=a+b·i – алгебраическая форма записи комплексного числа.

Пользуясь алгебраической формой записи комплексного числа, легко показывается, что произведение комплексных чисел иможно вычислить по правилу умножения многочлена на многочлен с заменойi² на -1.

с₁·с₂ = (а₁+b₁·i)·(а₂+b₂·i)=а₁·а₂+а₁·b₂·i+а₂·b₁·i +b₁·b₂·i² =

= (а₁·а₂-b₁·b₂)+i(а₁·b₂+а₂·b₁) = (а₁·а₂-b₁·b₂,а₁·b₂+а₂·b₁)

Комплексные числа иназываютсясопряженными числами.

Легко доказывается, что операция сопряжения обладает свойствами:

1. 

2. 

3. 

4. 

Произведение , неравенство будет строгим, если с ≠ 0. Во множестве комплексных чисел существует единственное число , такое что, и в множестве комплексных чисел существует единственное число, что.

Пусть с₁ = а₁+b₁·i и с₂ = а₂+b₂·i , причем с₂ ≠ 0, тогда частное , таким образом будет найдено частное.

Геометрические изображения комплексных чисел

Рассмотрим декартову числовую плоскость.

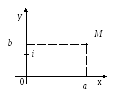
Изобразим комплексное число с = (a,b) = a+i·b точкой М(a,b). Эту точку М мы будем называть аффиксом комплексного числа с = (a,b) (аффикс – отметка). В дальнейшем эти точки мы будем также обозначать буквой с, и отождествлять комплексные числа с соответствующими точками декартовой плоскости.

Плоскость, точки которой являются изображением комплексных чисел, называется комплексной плоскостью, ее обозначают символами (Z) или (W).

Легко видеть, что действительные числа а = (а,0) изображаются точками оси иксов (oX), поэтому ось абсцисс называется действительной осью.

Мнимые числа с = (a,b) = a+i·b (b ≠ 0) изображаются точками, не лежащими на оси абсцисс. Чисто мнимые числа c = (0,b) = b·i (b ≠ 0) изображаются точками оси ординат, поэтому эту ось в комплексной плоскости называют мнимой осью.

Начало координат (0,0) является изображением комплексного числа 0, поэтому оно называется нулем. Отметим, что комплексные числа Z=x+i·y=(x,y) также изображаются векторами плоскости с проекциями x и y. Начало вектора может быть помещено в любую точку.

Изобразим комплексное число Z = (x,y) = x+i·y вектором, начало которого помещено в нуль.

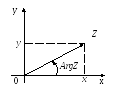
Длина этого вектора очевидно равна и называетсямодулем комплексного числа Z и обозначается .

Угол, который составляет этот вектор с положительным направлением действительной оси, называется аргументом комплексного числа Z и обозначается ArgZ. Этот угол определяется неоднозначно, а с точностью до слагаемых кратных 2π. Отметим, что направление отсчета углов против часовой стрелки принимают за положительное, а по часовой стрелке за отрицательное.

Среди бесконечного множества значений ArgZ есть одно такое, которое содержится в полуинтервале , оно называетсяглавным значением аргумента числа Z и обозначается символом argZ.

Очевидно ArgZ = argZ+2πk (к = 0, 1,2,…). Легко доказывается, что для комплексных чисел Z = x+y·i

argZ =