4. Основные свойства определенного интеграла

Если коротко говорить, то основные свойства в этом случае, в основном, совпадают с основными свойствами неопределенного интеграла. Перечислим их:

1.

2. . Интеграл суммы равен сумме интегралов.

3. .

4. если a<c<b,то. Это свойство называют аддитивностью определенного интеграла.

5. Теорема о среднем.Еслинепрерывна на отрезке, то существует такая точка, что.

Доказательство:

По формуле Ньютона-Лейбница имеем , где. Применяя к разноститеорему Лагранжа, получим, но, т.е.ч.т.д.

Число называют средним значением функции на отрезке.

6. Если функция сохраняет знак на отрезке, то интегралимеет тот же знак, что и функция. Так еслина, то.

7. Неравенство между непрерывными функциями на отрезке можно интегрировать. Так еслипри, то. Отметим, что дифференцировать неравенства нельзя.

8. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции. ,a<b.

9. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, т.е. .

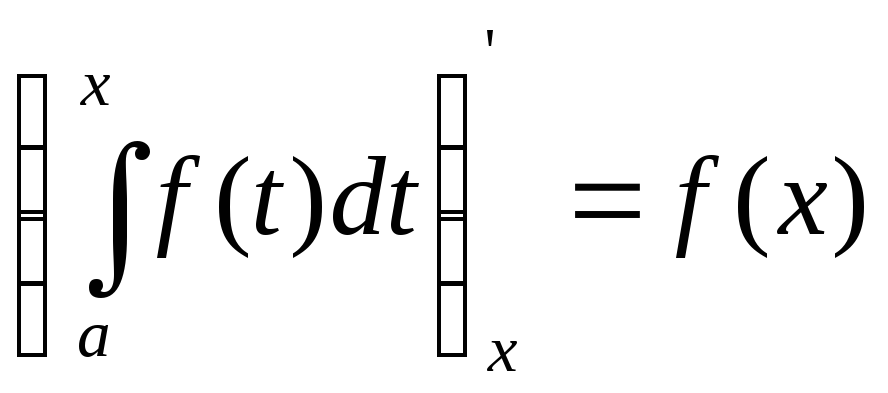Доказательство:

По формуле Ньютона-Лейбница . Следовательно,. Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.

4. Вычисление определенного интеграла

1) Наиболее простым способом вычисления определенного интеграла является формула Ньютона-Лейбница. Применить этот способ можно во всех случаях, когда может быть найдена первообразная функции для подынтегральной функции. При вычислении определенных интегралов широко используются методы замены переменной интегрирования по частям.

а) Интегрирование подстановкой

Пусть для вычисления интеграла от непрерывной функции сделана подстановка. Причем, аи, тогда.

Пример. Вычислить. Положим, тогда, если, то, если, то. Поэтому

.

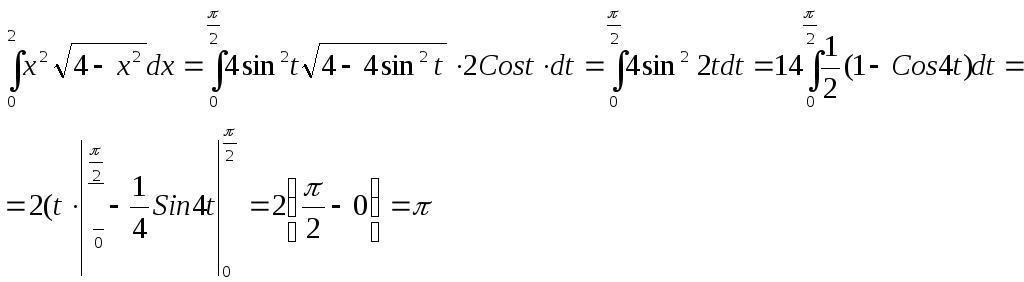б) Интегрирование по частям

Теорема: Если функцияиимеют непрерывные производные на отрезке, то должно выполняться соотношение:

- формула интегрирования по частям.

Доказательство.

На отрезке имеет место равенство. Следовательно, функция- есть первообразная для непрерывной функции, тогда по формуле Ньютона-Лейбница имеем:

отсюда

ч.т.д.

Пример.

Положим

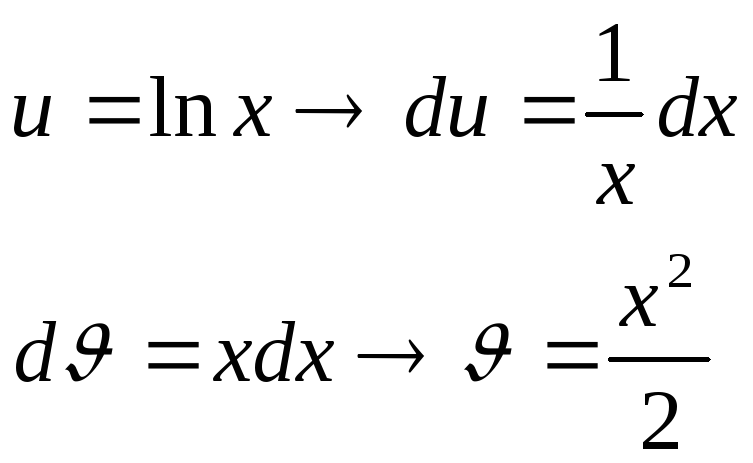
Применяя метод интегрирования по частям, получим:

.

4. Несобственные интегралы

Определенный интеграл , где промежуток интегрирования конечный, а подынтегральная функция непрерывна на, называетсясобственным.Рассмотрим так называемыенесобственныеинтегралы, т.е. интегралы от непрерывных функций, но с бесконечным промежутком интегрирования или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв.

1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл 1^огопорядка).

Пусть функция непрерывна на промежутке. Если существует конечный предел,то его называют несобственным интегралом первого порядка и обозначают. Таким образом,=.

В этом случае говорят, что несобственный интеграл сходится. Если же указанный предел не существует или он бесконечен, то говорят, что интегралрасходится.

Аналогичным образом определяется несобственный интеграл на промежутке .=. Несобственный интеграл с двумя бесконечными пределами определяется формулой:

+, где С – произвольное число. В этом случае интеграл слева сходится лишь тогда, когда сходятся оба интеграла справа. Отметим, что если непрерывная функцияна промежуткеи интегралсходится, то он выражает площадь бесконечно длинной криволинейной трапеции.

Пример:вычислить несобственный интеграл.

а) интеграл сходится

б) интеграл расходится, т.к.не существует.

2) Интеграл от разрывной функции (несобственный интеграл 2^огорода)

Пусть функция непрерывна наи имеет бесконечный разрыв приx=b. Если существует конечный предел, то его называют несобственным интегралом второго рода и обозначают. Таким образом, по определению

=. Если предел в правой части существует, то несобственный интегралсходится. Если же указанный предел не существует или бесконечен, то интегралрасходится. Аналогично, если функциятерпит бесконечный разрыв в точкеx=a, то=. Если функциятерпит разрыв во внутренней точке отрезка, то несобственный интеграл второго рода определяется соотношением+. В этом случае интеграл слева называется сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.

Пример:Вычислить, при х=0, функциятерпит бесконечный разрыв.

. Следовательно, интеграл расходится.