
- •Лекция 1 Функции нескольких переменных
- •Функция двух переменных
- •Предел функции
- •Непрерывность функции двух переменных
- •Производные и дифференциалы функции нескольких переменных
- •Частные производные высших порядков
- •Дифференцируемость и полный дифференциал функции
- •Дифференциалы высших порядков
- •Производная сложной функции. Полная производная
- •8.Инвариантность формы полного дифференциала
- •Дифференцирование неявной функции
- •Производная по направлению
- •Градиент
- •Экстремум функции двух переменных
- •Необходимые и достаточные условия экстремума
- •Лекции №№2,3
- •II. Неопределенный интеграл
- •2. Свойства неопределенного интеграла
- •3. Таблица основных неопределенных интегралов
- •4. Основные методы интегрирования
- •5. Интегрирование рациональных функций.
- •6. Интегрирование тригонометрических функций
- •7. Интегрирование иррациональных функций
- •Лекция 4
- •III. Определенный интеграл
- •Определение определенного интеграла
- •Геометрический смысл определенного интеграла
- •3) Работа переменной силы
- •Формулы Ньютона-Лейбница
- •Основные свойства определенного интеграла
- •Вычисление определенного интеграла
- •Несобственные интегралы
- •Лекция 5
- •7. Применение определенных интегралов для расчета геометрических и физических величин различного рода
- •7.1. Вычисление площадей плоских фигур
- •7.2 Вычисление длины дуги плоской кривой
- •7.3 Вычисление объема тела
- •8. Приближенное вычисление определенного интеграла
- •8.1. Формулы прямоугольников
- •8.2. Формула трапеций
- •8.3. Формула парабол (Симпсона)
- •Лекция 6,7
- •4. Кратные интегралы
- •4.1. Двойной интеграл. Основные понятия
- •4.2. Геометрический смысл двойного интеграла
- •4.3. Основные свойства двойного интеграла
- •4.4.Вычисление двойного интеграла
- •4.5. Приложения двойного интеграла
- •4.6. Тройной интеграл. Основные понятия
- •4.7. Вычисление тройного интеграла.
- •4.8. Приложения тройного интеграла
- •Лекция 8
- •V. Числовые ряды
- •5.1. Основные понятия
- •5.2. Необходимый признак сходимости числового ряда
- •5.3. Достаточные признаки сходимости знакопостоянных рядов
- •5.4. Признак Даламбера
- •5.5. Радикальный признак Коши
- •5.6. Интегральный признак Коши. Обобщенный гармонический ряд
- •5.7. Знакочередующиеся и знакопеременные ряды Признак Лейбница
- •Общий достаточный признак сходимости знакопеременных рядов
- •5.8. Абсолютная и условная сходимость числовых рядов
- •Лекция №9 Степенные ряды
- •1 Функциональные ряды
- •1.1 Основные понятия
- •2. Некоторые приложения степенных рядов
- •2.1. Приближенное вычисление значений функций
- •2.2. Приближенное вычисление определенных интегралов
- •Лекция №10
- •VII Ряды Фурье
- •7.1. Основные понятия
- •7.2. Тригонометрический ряд Фурье
- •7.3 Разложение в ряд Фурье 2π-периодических функций. Теорема Дирихле
- •7.4. Разложение в ряд Фурье четных и нечетных функций
- •7.5. Разложение в ряд Фурье функций произвольного периода
- •Лекция 11.
- •VIII. Дифференциальные уравнения (д.У.)
- •8.1. Общие сведения на основании понятия о д.У.
- •8.2. Дифференциальное уравнение первого порядка
- •2. Метод Лагранжа
- •Лекция 12
- •8.3.Дифференциальные уравнения высших порядков
- •1.Решение путем понижения порядка уравнения.
- •2.Линейные дифференциальные уравнения высших порядков.
- •8.4. Решение ду второго порядка с постоянными коэффициентами.
- •1.Решение лоду второго порядка с постоянными коэффициентами.
- •Лекция 13
- •2. Решение лоду n –го порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения (лнду)
- •1.Структура общего решения лнду второго порядка.
- •2.Метод вариации произвольных постоянных.
- •3.Решение лнду второго порядка с постоянными коэффициентами и правой частью специального вида.
- •4.Решение лнду n- го порядка с постоянными коэффициентами и правой специальной частью.
- •Лекция 14
- •2.Системы линейных ду с постоянными коэффициентами.
5.7. Знакочередующиеся и знакопеременные ряды Признак Лейбница
Рассмотрим важный
класс рядов, называемых знакочередующимися.
Такими рядами называется ряд вида:
![]() ,
где
,
где![]() для всех
для всех![]() .
Для знакочередующихся рядов имеет место
достаточный признак сходимости (Признак
Лейбница).
.
Для знакочередующихся рядов имеет место
достаточный признак сходимости (Признак
Лейбница).
Теорема Лейбница. Знакочередующийся ряд сходится, если:
последовательность абсолютных величин членов ряда монотонно убывает, т.е.
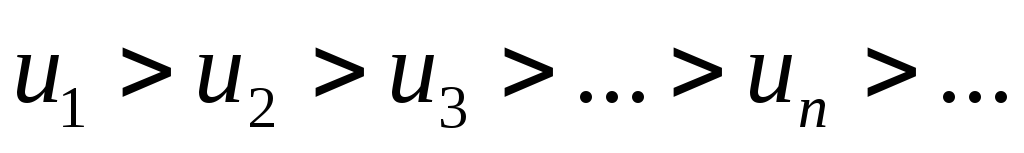
общий член ряда стремится к нулю
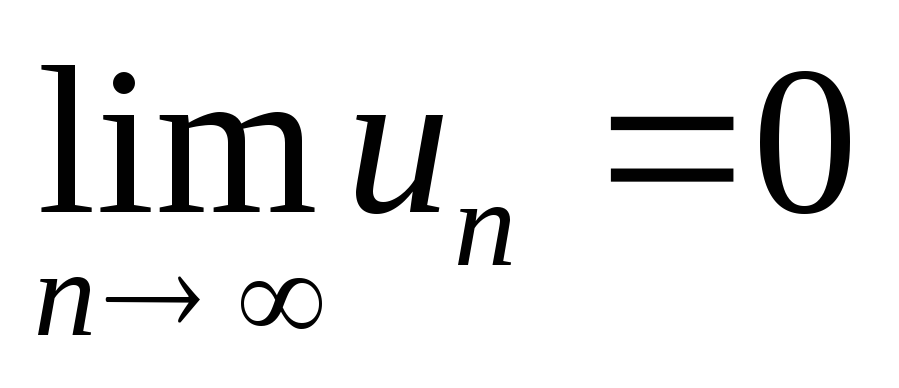 .
При этом сумма
.
При этом сумма ряда
удовлетворяет неравенствам
ряда
удовлетворяет неравенствам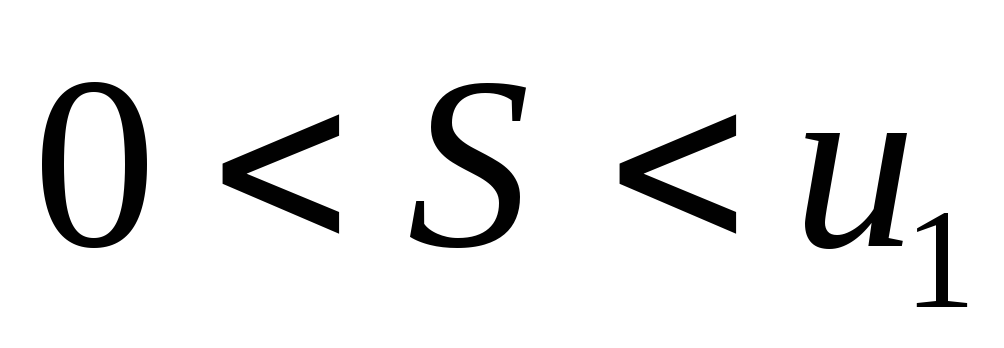 .
.
Доказательство:
Рассмотрим сначала
частичную сумму четного числа
![]() членов ряда. Имеем
членов ряда. Имеем![]() .
Выражения в каждой скобке согласно
первому условию теоремы положительно.
Следовательно, сумма
.
Выражения в каждой скобке согласно
первому условию теоремы положительно.
Следовательно, сумма![]() и
возрастает с возрастанием номера
и
возрастает с возрастанием номера![]() .
.
С другой стороны
![]() ,
можно переписать так:
,
можно переписать так:![]() .
Легко увидеть, что
.
Легко увидеть, что![]() . Таким образом, последовательность
. Таким образом, последовательность![]() возрастает и ограничена сверху.
Следовательно, она имеет предел
возрастает и ограничена сверху.
Следовательно, она имеет предел![]() ,
причем
,
причем![]() .
.
Рассмотрим теперь
частичные суммы нечетного числа
![]() членов ряда. Очевидно, что
членов ряда. Очевидно, что![]() .
Отсюда следует, что
.
Отсюда следует, что![]() .
Т.к.
.
Т.к.![]() в
силу второго условия теоремы. Итак,
в
силу второго условия теоремы. Итак,![]() как при четном
как при четном![]() ,
так и при нечетном
,
так и при нечетном![]() .
Следовательно, наш ряд сходится, причем
.
Следовательно, наш ряд сходится, причем![]() .
.
Замечания.
Исследование знакочередующихся рядов вида
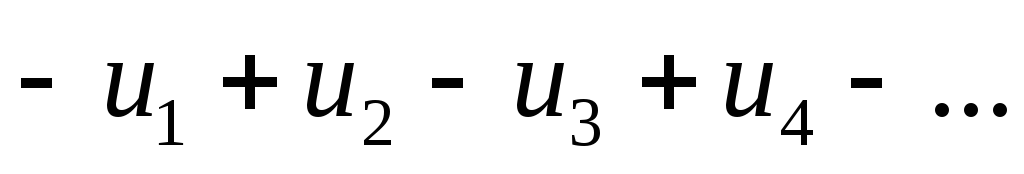 (с отрицательным первым членом) сводится
путем умножения всех его членов на (-1)
к исследованию ряда с + первым членом.
(с отрицательным первым членом) сводится
путем умножения всех его членов на (-1)
к исследованию ряда с + первым членом.Соотношение
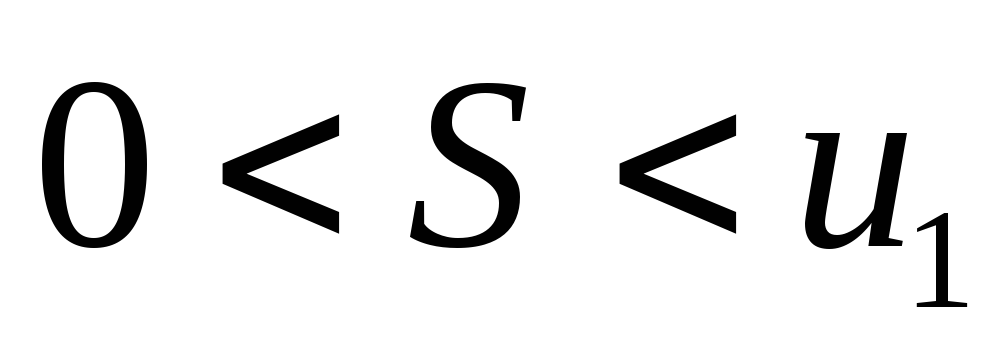 позволяет получить простую и удобную
оценку ошибки, которую мы допускаем,
заменяя сумму
позволяет получить простую и удобную
оценку ошибки, которую мы допускаем,
заменяя сумму данного ряда его частичной суммой
данного ряда его частичной суммой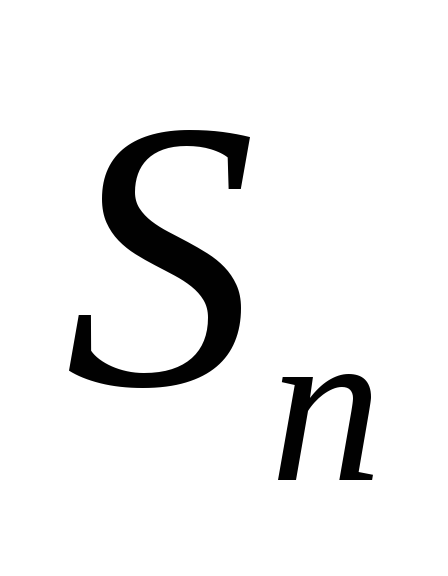 .
Отброшенный ряд представляет собой
также знакочередующийся ряд, сумма
которого по модулю меньше первого члена
этого ряда, т.е.
.
Отброшенный ряд представляет собой
также знакочередующийся ряд, сумма
которого по модулю меньше первого члена
этого ряда, т.е. поэтому
ошибка меньше модуля первого из
отброшенных членов.
поэтому
ошибка меньше модуля первого из
отброшенных членов.
Пример.
Вычислить сумму
ряда
![]() .
Данный ряд лейбницевского вида. Он
сходится. Можно записать
.
Данный ряд лейбницевского вида. Он
сходится. Можно записать![]() .
Взяв 5 членов, т.е. заменив
.
Взяв 5 членов, т.е. заменив![]() на
на![]() сделаем ошибку, меньшую чем
сделаем ошибку, меньшую чем![]() .
Итак,
.
Итак,![]() .
.
Общий достаточный признак сходимости знакопеременных рядов
Знакочередующийся
ряд является частным случаем
знакопеременного ряда. Числовой ряд
![]() ,
содержащий бесконечное множество
положительных и бесконечных множеств
отрицательных членов, называетсязнакопеременным.
Для
знакопеременных рядов имеет место
следующий общий достаточный признак
сходимости.
,
содержащий бесконечное множество
положительных и бесконечных множеств
отрицательных членов, называетсязнакопеременным.
Для
знакопеременных рядов имеет место
следующий общий достаточный признак
сходимости.
Теорема. Пусть
дан знакопеременный ряд
![]() .
Если сходится ряд
.
Если сходится ряд![]() ,
составленный из модулей членов данного
ряда, то сходится и сам знакопеременный
ряд.
,
составленный из модулей членов данного
ряда, то сходится и сам знакопеременный
ряд.
Доказательство:
Рассмотри
вспомогательный ряд, составленный из
членов рядов
![]() и
и![]() .
.
![]() .
.
Очевидно, что
![]() для
всех
для
всех![]() ,
но ряд
,
но ряд![]() сходится в силу условий теоремы исвойства 1
числовых рядов. Следовательно, на
основании признака сравнения сходится
и ряд
сходится в силу условий теоремы исвойства 1
числовых рядов. Следовательно, на
основании признака сравнения сходится
и ряд
![]() .
Поскольку данный знакопеременный ряд
представляет собой разность двух
сходящихся рядов
.
Поскольку данный знакопеременный ряд
представляет собой разность двух
сходящихся рядов![]() ,
то на основаниисвойства
2 числовых
рядов ряд
,
то на основаниисвойства
2 числовых
рядов ряд
![]() сходится.
сходится.
Отметим, что
обратное утверждение несправедливо:
если сходится ряд
![]() ,
то это не означает, что сходится ряд
,
то это не означает, что сходится ряд![]() .
.
Пример.
Исследовать
сходимость ряда
![]() .
Для этого ряда выполнены условия признака
Лейбница. Следовательно, ряд сходится.
Однако ряд, составленный из модулей
членов этого ряда, т.е.
.
Для этого ряда выполнены условия признака
Лейбница. Следовательно, ряд сходится.
Однако ряд, составленный из модулей
членов этого ряда, т.е.![]() расходится (гармонический ряд).
расходится (гармонический ряд).
5.8. Абсолютная и условная сходимость числовых рядов
Знакопеременный ряд называют абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. Знакопеременный ряд называют условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место: на такие ряды переносятся основные свойства конечных сумм (переместительность, сочетательность, распределительность).
Т.е. абсолютно сходящиеся ряды суммируются, вычитаются как обычные ряды. Суммы таких рядов не зависят от порядка записи членов. В случае условно сходящихся рядов, такие свойства, вообще говоря, не имеют места.
